Es lebe die Geometrie!

Höhen im hyperbolischen 6-Rechteck
und seinem stereografischen Bild

Auf der vorangehenden Seite ' Kugelviereck 3' wurde ein Viereck ABCD mit nicht komplanaren Eckpunkten
auf der Oberfläche K der Kugel um den Ursprung vom Radius 1 untersucht. In einer Gleitschau wurde dabei
gezeigt, wie man im stereografischen Bild von ABCD das stereografische Bild der Geraden
g mit Zirkel und Lineal konstruiert, die sowohl die Gerade AB als auch die Gerade CD hyperbolisch
orthogonal schneidet. Wir nennen eine derartige Gerade 'Achse' von AB und CD. Auf g liegt dann der Pol
bezüglich K von einer Ebene durch AB und auch der Pol einer Ebene durch CD. Die zu g polare Gerade
h ist ebenfalls Achse von AB und CD. Auf h liegen genau die Punkte, die Pole einer Ebene durch g sind.
Die zueinander polaren Achsen von BC und DA, sowie von AC und BD treffen mit g und h jeweils zu dritt
paarweise hyperbolisch orthogonal aufeinander. Die vier Treffpunkte Z0, Z1, Z2 und Z3 wurden als farbige
Quadrate eingezeichnet, bei Z0, Z1, Z2 außerhalb K mit weißem Kern und bei Z3 innerhalb K mit schwarzem
Kern.

Auf dieser Seite wenden wir diese Konstruktion auf ein hyperboliches 6-Rechteck ABCDEF im Innern von
K an. Wenn man von drei paarweise nicht komplanaren Geraden ausgeht und zu jedem Paar dieser Geraden
eine der beiden zueinander polaren Achsen auswählt, bilden die Lotfußpunkte dieser Achsen ein hyperbolisches
6-Rechteck. Die Achsen zu gegenüberliegenden Seitengeraden von ABCDEF stellen die Höhen in diesem
6-Rechteck dar.

Gegenüber der entsprechenden Konstruktion auf der Seite ' Höhen im 6-Rechteck' für euklidische Raumgeraden
kommt auf dieser Seite durch die Betrachtung des stereografischen Bildes ein neuer Aspekt hinzu. Denn dieses
Bild gibt in der Ebene die räumliche Konfiguration ohne Informationsverlust wieder. Unten auf dieser Seite wird
gezeigt, dass man die zugehörigen algebraischen Rechnungen ohne den Umweg über die Koordinaten-Tripel der
Raumgeraden durchführen kann.

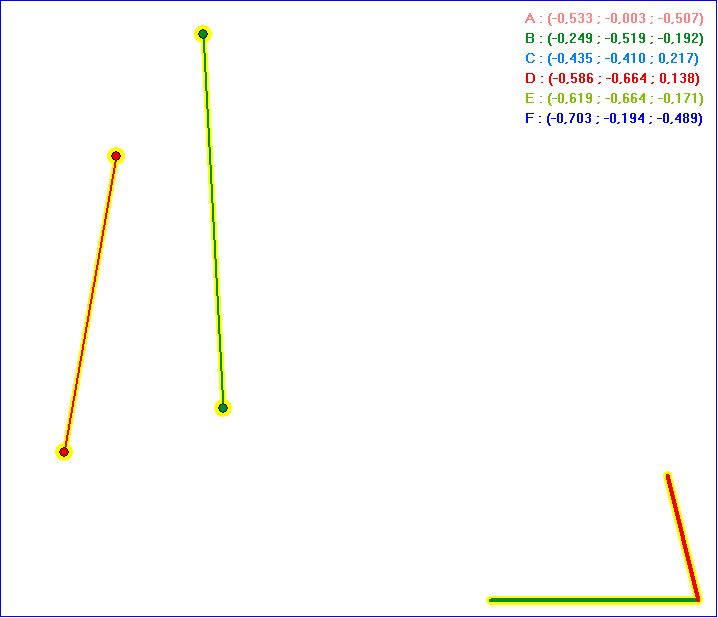
Die Gleitschau zeigt in der ersten Hälfte den Aufbau des stereographischen Bildseines
6-Rechtecks ABCDEF mit zuhehörigen Höhen im Innern von K. Alle Punkte liegen in der Bildebene E
der stereografischen Projektion mit der Gleichung x = 1. Parallel dazu wird unten rechts die Entwicklung
eines Dreiecks in der euklidischen Ebene dargestellt, wobei den Eckpunkten die Seiten-Geraden ,
und entsprechen. In der zweiten Hälfte der 74 Bilder der Gleitschau wird die Konstruktion
der ersten Hälfte analog im Raum durchgeführt. Das Bild entsteht dann durch Parallel-Projektion auf die
Ebene E, die man sich als die Ebene des Bildschirms vorstellen kann. In der zweiten Hälfte gehen wir von
den Schnittpunkten der Kanten-Geraden BC, DE und FA mit K aus und in der ersten Hälfte von den
stereografischen Bildern dieser Punkte. Die Eckpunkte ABCDEF und sind in der Farbe
dieser Buchstaben mit einem weißen Hof markiert. Die Kanten-Geraden bzw. Seiten-Geraden sind
durch die Strecken zwischen den zugehörigen Schnittpunkte mit K bzw. deren stereografischen Bildern
kenntlich gemacht.

Das erste Bild der Gleitschau zeigt die Bilder der Kanten-Geraden BC und DE. Sie sind gelb unterlegt, um
auszudrücken, dass im Folgenden das stereografische Bild der Achse von BC und DE konstruiert wird.
Dazu werden im zweiten Bild die Punkte , und nicht sichtbar , benutzt, die man wie in der
Gleitschau am Schluss der Seite ' Kugelviereck 3' konstruiert. Die grauen Geraden und
sind euklidisch orthogonal, da sie stereografische Bilder der zueinander polaren Geraden und
sind. Das dritte Bild zeigt zwei hellblaue Kreise durch die roten bzw. grünen Kugelpunkt-Bilder, deren
Mittelpunkt sich als Schnittpunkt der Mittelsenkrechten mit der Geraden ergibt. Die eingezeichneten
Tangenten treffen sich mit der zugehörigen Mittelsenkrechten auf der Geraden . Die Kugelpunkt-
Bilder der Geraden sind die Schnittpunkte der hellblauer Kreise auf . bzw. ist der
Schnittpunkte von mit bzw. .

Im sechsten Bild wird das stereografische Bild der Kanten-Gerade FA hinzugefügt und anschließend die
Gerade konstruiert, woraus sich im siebenten Bild die Strecke ergibt. , und
und die Höhen folgen nach dem gleichen Muster. In den letzten acht Bildern der ersten Hälfte der
Gleitschau wird gezeigt, dass die drei Höhen eine gemeinsame Achse haben, indem die Achsen für zwei
verschiedene Höhen-Paare konstruiert werden.

In der zweiten Hälfte der Gleitschau, in der die Bilder der Parallel-Projektion für die analoge Konstruktion
im Raum gezeigt werden, sind die Mittelpunkte der Kreise der ersten Hälfte durch Pole von Ebenen ersetzt,
die K in Kreisen schneiden. Diese erscheinen bei der Parallel-Projektion als Ellipsen. Jeder Pol ist im Raum
kollinear mit dem zugehörigen Mittelpunkt und dem Zentrum N(-1;0;0) der stereografischen Projektion. Der
Inzidenz eines Kreis-Mittelpunkts mit einer Geraden entspricht die Inzidenz des zugehörigen Pols mit
. Dies bedeutet, dass die Ebene zum Pol hyperbolisch orthogonal zu ist.
Wie auch die Gerade liegen einige Pole zum Teil außerhalb des Bildes.

Die gemeinsame Achse der Höhen kann bei einer Bestimmung der hyperbolischen Raumgeraden mit Hilfe
von Tripeln komplexer Zahlen mit dem gleichen Term berechnet werden, wie die Höhen-Achse bei einem
euklidischen 6-Rechteck auf der Seite 'euklidische Raumgeraden > Höhen im 6-Rechteck', nämlich
. Dabei ist s bzw. u bzw. w das Tripel aus komplexen Zahlen der Kanten-
Gerade zu BC bzw. DE bzw. FA. Der Übergang von einer euklidischen in eine hyperbolische Maß-
Bestimmung verlangt also nur den Wechsel der Dualzahl mit in die komplexe Zahl i mit .
Um ein Geraden-Tripel zu erhalten, muss der Term m allerdings noch k-normiert werden, indem man ihn
durch die Wurzel des inneren Produkts mit sich selbst dividiert.

Die Animation zeigt den Übergang vom stereografischen Bild zum räumlichen 6-Rechteck
ABCDEF, dessen Drehung um 360° und den Übergang zurück zu . Für den Übergang
wurde in jedem Zwischen-Zustand jede Strecke zwischen Urbild- und Bild-Punkt im gleichen Verhältnis
geteilt. Das hat zur Folge, dass Punkte, die im Anfangs- und im End-Zustand gemeinsam auf einer
Geraden liegen, die Kollinearität im Zwischen-Zustand verlieren.

Diese Animation zeigt entsprechend der vorherigen den Übergang zum stereografischen Bild mit der
Ergänzung der Raumgeraden, die im Analogie-Dreieck unten rechts dem Höhenfußpunkt-Dreieck
und den Eckpunkte-Loten dazu entsprechen. Die diesen Loten entsprechenden Raumgeraden
haben wie im Fall der euklidischen Maße auch hier eine gemeinsame Achse. Nach der ersten
Hälfte der Animation werden die Koordinaten-Tripel von ABCDEF zum jeweils vorangehenden
Punkt zyklisch verschoben. Dies drückt sich in der Zeichnung darin aus, dass die Farbe jeder
Kante in die Farbe der vorangehenden Kante wechselt. An der Lage der Höhen ändert sich dann
nichts, wohl aber an dem 6-Rechteck, das dem Höhenfußpunkt-Dreieck entspricht, da bei ABCDEF
punkt-analoge und geraden-analoge Kanten vertauscht sind. Dies drückt sich in der Farbgebung des
Analog-Dreiecks unten rechts aus.

Die Gleitschau zeigt nach den Standbildern der Animation im drittletzten Bild auch die polaren Höhe,
welche die Kugel K nicht treffen. Die beiden letzten Bilder zeigen Maße, deren Zusammenhang die
Analogie zu den euklidischen Maßen sowohl in dem Analogie-Dreieck als auch in dem euklidischen
6-Rechteck auf der Seite ' Höhenfußpunkte' verdeutlicht. Siehe dazu auch die nächste Seite
' Winkelhalbierende im 6-Rechteck'.

Der geometrische Zusammenhang zwischen der gemeinsamen Achse der drei Höhen und der von den
"Eckpunkt"-Loten ist der Gleiche wie bei euklidischen Raumgeraden und auch wie in der ebenen Dreicks-
Geometrie. In dem Analogie-Dreieck unten rechts sind nämlich die beiden violetten Punkte isogonal
konjugiert. Denn die Lotgerade von z. B. A zum Höhenfuß-Dreieck ergibt sich, indem man an der Seite
AE den Winkel zwischen der Höhe durch A und der Seite AC abträgt, und mit den anderen Ecken
analog verfährt. Wir nennen die Lotgerade 'vierte Spiegelungsgerade' zu AE, Höhe, AC (in dieser
Reihenfolge). Diese Bezeichnung wird nur benutzt, wenn die Hintereinanderschaltung der Spiegelungen
an diesen drei Geraden mit der Spiegelung an der vierten Geraden übereinstmmt. Wenn man nur die
Spiegelungen an den ersten beiden Geraden hintereinanderschaltet, ergibt sich eine Drehung mit einem
Drehwinkel, der doppelt so groß ist wie der Winkel zwischen den beiden Geraden. Diese Bezeichnungen
übertragen wir analog auf die Raumgeraden, wobei die Drehung durch eine Schraubung ersetzt wird,
die sich als Hintereinanderschaltung einer hyperbolischen (oder euklidischen) Drehung und einer
hyperbolischen (oder euklidischen) Verschiebung ergibt. Diese Hintereinanderschaltung ist ebenfalls
als Hintereinanderschaltung zweier Geraden-Spiegelungen darstellbar, deren räumlicher Zusammenhang
durch den halben Drehwinkel und die halbe Verschiebungslänge bestimmt ist.

Die beiden violetten Achsen zu den Höhen und den "Eckpunkt"-Loten bezeichnen wir also ebenfalls als
'isogonal konjugiert'. Zwischen derartigen Geraden gibt es bei hyperbolischen Raumgeraden den analogen
algebraischen Zusammenhang wie für euklidische Raumgeraden. Den Kanten-Geraden BC, DE und FA
des 6-Rechtecks ABCDEF seien Tripel komplexer Zahlen s, u und w zugeordnet, die nicht notwendig
k-normiert sind. Zu einem Geraden-Tripel p sei definiert .
Dann gehört q zu der isogonal konjugierten Geraden. q ist allerdings im Allgemeinen noch nicht k-normiert.
Falls p zur Höhen-Achse gehört, ist
.

Berechnungen geometrischer Konfigugrationen in der Bildebene
der stereografischen Projektion

g sei eine hyperbolische Raumgerade, die K in zwei verschiedenen Punkten P und Q ungleich N schneidet.
Die Bilder von P und Q bei der stereografischen Projektion seien die Punkte mit den Tripeln und
aus reellen Zahlen. Die beiden komplexen Zahlen und sind
Lösungen der quadratischen Gleichung oder auch der Gleichung, die entsteht,
wenn man den Term auf der linken Seite mit einer komplexen Zahl ungleich Null multipliziert. Das komplexe
Koeffizienten-Tripel oder ein Tripel, das daraus entsteht, dass man es mit einer
komplexen Zahl multipliziert, nennen wir 'Polynom-Tripel' von g. Wenn die dritte Komponente 1 ist,
nennen wir das Polynom-Tripel 'normiert'. Damit das zugehörige Polynom zwei verschiedene Lösungen
hat, müssen die dritte Komponente des Tripels und die Diskriminante ungleich Null sein. Das Tripel muss
von dem Tripel komplexer Zahlen unterschieden werden, das wir 'Geraden-Tripel' nennen und sich aus den
Plücker-Koordinaten der Geraden zusammensetzt, entsprechend der Erklärung auf der Seite ' Orthogonalität'.
Die beiden Tripel stehen aber in einem einfachen algebraischen Zusammenhang, der im Folgenden gezzeigt wird.

P und Q haben die Koordinaten-Quadrupel und
. Für g ergibt sich daraus das Geraden-Tripel






Wenn man durch teilt, ergibt sich .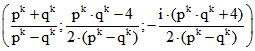
Dies ist ein Geraden-Tripel u von g mit . Wenn mit und
normiertes Polynom-Tripel von g ist, dann ist ein Geraden-Tripel von g,
das allerdings im Allgemeinen nicht k-normiert ist. Um ein Geraden-Tripel für ein nicht normiertes Polynom-
Tripel zu erhalten, ersetzt man im Geraden-Tripel für das normierte Polynom-Tripel
und durch und und multipliziert das entstandene Tripel mit . Mit der Matrix
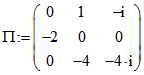ergibt sich die invertierbare lineare Abbildung
,
die jedem Polynom-Tripel eines Polynoms mit zwei verschiedenen Nullstellen ein Geraden-Tripel einer Geraden
zuordnet, die K in zwei verschiedenen Punkten trifft und nicht mit N inzidiert. Die Nullstellen sind die komplexen
Zahlen, deren Real- bzw. Imaginärteil die y- bzw. z-Komponente der stereografischen Bilder in der Ebene x = 1
angeben.

Diese Abbildung ermöglicht eine einfache Übertragung der algebraischen Beziehungen zu geometrischen
Relationen für hyperbolische Raumgeraden in algebraische Beziehungen für Polynome, deren Nullstellen
stereografische Bilder der Schnittpunkte der Geraden mit K bestimmen.

Geraden g, h mit den Geraden-Tripeln u und v schneiden sich genau dann hyperbolisch orthogonal,
wenn das innere Produkt ist. Für Polynom-Tripel
und ist . Die Orthogonalität ist folglich
äquivalent mit . Normierte Polynom-Tripel
und sind also orthogonal genau dann, wenn .

Eine Achse, die g und h beide hyperbolisch orthogonal schneidet, hat das Geradentripel
. Zu den Polynom-Tripeln a und b
gehört die Achse ,

Geraden g, h, j mit den Geraden-Tripeln u, v, w haben eine gemeinsame Achse oder einen gemeinsamen
Punkt auf K genau dann, wenn die Determinante Det((u, v, w)) Null ist. Dies gilt entsprechend für
Polynom-Tripel a, b, c , da .

Wenn g, h, j eine gemeinsame Achse haben oder einen gemeinsamen Punkt auf K, dann hat die vierte
Spiegelungsgerade k von g, h, j das Geraden-Tripel . Die Spiegelung
an k stimmt dann mit der Hintereinanderschaltung der Spiegelungen an g, h, j überein.
Das zugehörige Polynom-Tripel ist .

Zum komplexen Geraden-Tripel u definieren wir die Matrix ,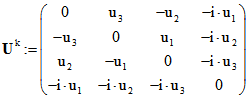
wobei i die imaginäre Einheit ist. s sei das Quadrupel eines Punktes S. Dann hat der Punkt T,
der durch Spiegelung von P an der Geraden g zum Tripel u entsteht, das Quadrupel , wobei
die Matrix ist, die entsteht, wenn man die Komponenten von durch die dazu konjugiert komplexen
Elemente ersetzt. Sei nun S eine Punkt von K mit dem Tripel des stereografischen Bildpunkts.
Sein Spiegelungspunkt T liegt dann auch auf K. Das Tripel des stereografischen Bildpunkts sei .
Sei , und 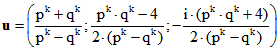das oben
hergeleitete Tripel mit den komplexen Zahlen und , die zu Schnittpunkten von g mit K gehören.
Dann gilt . Dies ist die gleiche Bedingung, die sich oben aus der
Orthogonalität von Polynom-Tripeln ergab.

Um auch die Spiegelungen an Geraden durch das Zentrum N(-1;0;0) der stereografischen Projektion zu
erfassen, ordnet man der komplexen Zahl die Gerade g durch P und N zu. Dann ist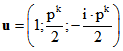
und die stereografische Übertragung der Spiegelung in die Ebene E ist durch
gegeben.


Auch eine Schraubung zur Winkel-Größe und der Verschiebungs-Länge d kann innerhalb des
Bildes der stereografischen Projektion dargestellt werden. Sei , und
. Dabei ist die Matrix mit vier Zeilen und Spalten, die nur Einsen in
der Hauptdiagonalen hat und sonst nur Nullen. Dann ist das Schraubungs-Bild eines Punktes S mit
dem Quadrupel s der Punkt mit dem Quadrupel (siehe auch die Seite ' Kugelviereck 2' )
und die Formel für die Spiegelung ändert sich zu
.

Wenn g die Gerade durch N und P ist zum Tripel 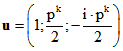, lautet die entsprechende Formel
.



.