Es lebe die Geometrie!

Hyperbolisches Paraboloid

Wir schließen hier an die erste Gleitschau auf der Seite ' Ceva' an, auf der das Analogon der Satzes
von Ceva für ein nicht komplanares Viereck ABCD benutzt wird, um ein einschaliges Hyperboloid zu
konstruieren. Der dort benutzte Wert 2 für die Teilverhältnis-Konstante tvk wird hier durch tvk = 1
ersetzt, so dass ein hyperbolisches Paraboloid QH entsteht. Wie beim Hyperboloid gibt es auch beim
Paraboloid zwei 'Regulusse' (Reguli), deren Geraden ganz in QH liegen. Jede Geraden des ersten
Regulus verbindet einen Punkt P auf der Geraden AB mit einem Punkt Q auf der Geraden CD, jede des
zweiten einen Punkt R auf DA mit einem Punkt S auf BC. Mit den Abkürzungen
und ausgedrückt, waren die Teilverhältnisse auf der Seite ' Ceva' für P, Q, R und S
, so dass das Produkt dieser vier Zahlen 1 ergibt und die Geraden PQ und RS sich
nach dem Analogon des Satzes von Ceva schneiden. Um für die Zeichnung Geraden zu den Werten r
und s auszuwählen, gaben wir eine natürliche Zahl n (z.B. n = 4) vor und benutzen für r und s nur
ganzzahlige Vielfache des Kehrwerts von n. Wir nennen dieses Verfahren hier 'Hyperboloid-Teilung'.
Für das Paraboloid führen wir eine weitere Teilung ein, die 'Paraboloid-Teilung'. Dabei ändert sich nur
die Formel für vr und vs. Wir setzen dann nämlich und . Für tvk = 1 teilen dann
P und Q bzw. R und S die Strecken AB und DC (nicht CD!) bzw. BC und AD (nicht DA!) im Verhältnis
vr bzw. vs. Für das Koordinaten-Tripel p von P gilt dann und Entsprechendes für Q, R
und S. Man erreicht damit eine gleichmäßige Unterteilung der Strecken, die dem Paraboloid zum Teil besser
angepasst ist als die Hyperboloid-Teilung.

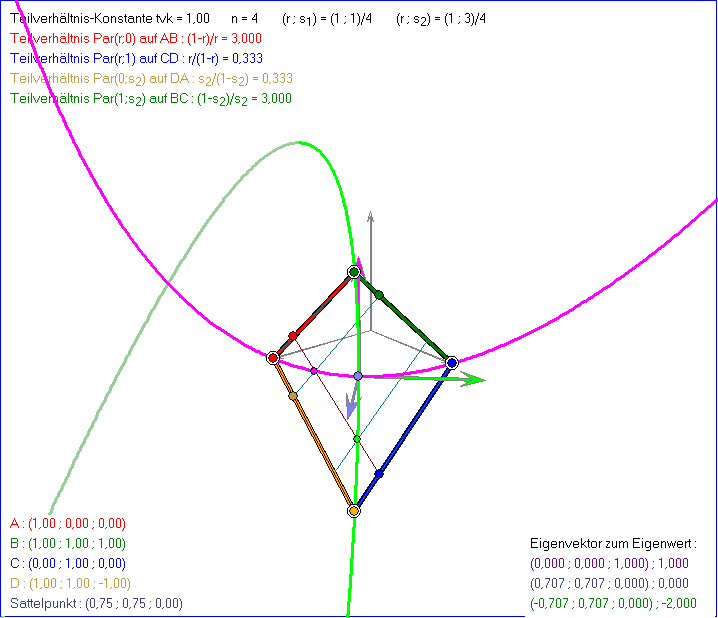
Im ersten Teil dieser Gleitschau wird die Paraboloid-Teilung mit den braunen Geraden Gx(r) des ersten
Regulus zu Werten von r durchgeführt, für die ganzzahlig ist. Für die blaugrünen Geraden Gy(s) des
zweiten Regulus ist 4s ganzzahlig, wobei die Zahlen 1, 2, 3, 4, 5... durchläuft und die Zahlen
3, 2, 1, 0, -1.... Die Schnittpunkte Par(r ; s) liegen dann auf der magentafarbenen bzw. hellgrünen Parabel
bzw. , die Schnittkurve von QH mit einer Symmetrie-Ebene von QH ist. Die beiden Parabeln
schneiden sich im Sattelpunkt S. Sie ist der einzige Schnittpunkt von QH mit der Symmetrie-Achse von QH.
Diese ist wegen der Symmetrie des in diesem Fall benutzten Standard-Vierecks ABCD die Verbindungs-
Gerade der Mittelpunkte von den Strecken AC und BD. In jedem Fall ist die Verbindungs-Gerade parallel
zur Symmetrie-Achse. Der hellblauen Eigenvektor von Fpred, der an S angeheftet ist, zeigt die Richtung
der Achse an. (Zu Fpred siehe die Erklärung am Schluss der vorangehenden Seite ' Hyperboloid 2'.) Der
hellgrüne bzw. magentafarbene Eigenvektor bzw. von Fpred ist euklidisch orthogonal zu der Ebene
der gleichfarbigen Parabel und außerdem Tangenten-Vektor der anderen Parabel. Die Koordinaten der
Vektoren sind unten rechts im Bild angegeben.

Im zweiten Teil der Gleitschau wird das letzte Bild des ersten Teils in verschiedenen räumlichen Ansichten
gezeigt. Erst wird es in die Vogel-Perspektive gedreht. In dieser Ansicht werden die Schnittkurven der
Ebenen zugefügt, die parallel sind zu den Symmetrie-Ebenen von QH durch die Teilungs-Punkte auf der
Geraden AB. Die hellgrünen Schnittkuven erscheinen hier geradlinig, sind im Raum aber Parabeln, die von
der Seite angesehen werden. Sie sind Parabeln, die aus durch Verschiebung des Scheitelpunkts S
auf entstehen. Analog ergeben sich die magentafarbenen Schnittkurven, indem man den Scheitelpunkt
S von auf verschiebt. Die Parabeln gleicher Farbe sind also kongruent. Die im dritten Bild der
Vogel-Schau zugefügten Regulus-Geraden treffen die Schnittpunkte der hellgrünen und magentafarbenen
Parabeln.

Nach diesen Ergänzungen wird die Vogel-Schau in eine Ansicht mit dem Augenpunkt auf der Symmetrie-
Achse von QH übergeführt, so dass beide Parabel-Scharen als geradlinige Diagonalen im Rauten-Muster
der Regulus-Geraden erscheinen. Anschließend wandert das Auge in der Ebene von bis zur Geraden
durch S orthogonal zur Ebene von , so dass die hellgrünen Parabeln unverzerrt erscheinen.

Im letzten Teil der Gleitschau wird der vorangehende Ablauf mit der Hyperboloid-Teilung an Stelle der
Paraboloid-Teilung wiederholt. Hier wird von den Schnittpunkte Hyp(r ; s) nicht mehr getroffen,
wohl aber die Parabel . In der Vogel-Perspektive werden dann nicht die Schnittkurven der Ebenen
parallel zu den Symmetrie-Ebenen von QH zugefügt, sondern die Schnittkurven der Ebenen durch drei
Punkte Hyp(r ; s), Hyp(r+1 ; s-1), Hyp(r-1 ; s+1), bzw. Hyp(r ; s), Hyp(r+1 ; s+1), Hyp(r-1 ; s-1).
Dies sind im Allgemeinen keine Parabeln, sondern Hyperbeln, die aber Diagonalen im Netz der Regulus-
Geraden darstellen.

Die Animation zeigt zunächst das Paraboloid zum Standard-Viereck ABCD bei einer Drehung um 360°.
Anschließend wird dargestellt, wie sich das Paraboloid verändert, wenn bei festgehaltenen Punkten A
und C die Punkte B und D symmetrisch um die Achse AC gedreht werden. Das Viereck ABCD, das
mit Paraboloid-Koordinaten r und s durch Par(0;0), Par(1;0), Par(1;1) und Par(0;1) beschrieben werden
kann, wird hier um weitere Viereckspunkte Par(i ; i-1), Par(i ; i) und Par(i-1 ; i) mit ganzzahligem i ergänzt.
Die magentafarbenen bzw. hellgrünen Parabeln ergeben sich aus den gleichfarbigen Parabeln durch den
Sattelpunkt S, die Schnittkurven mit Symmetrie-Ebenen von QH sind, durch Verschiebung des Scheitelpunkts
auf der andersfarbigen Symmetrie-Kurve. Sie stellen Diagonalen im Netz der Regulus-Geraden dar.

Das hyperbolische Paraboloid QH unterscheidet sich von dem einschaligen Hyperboloid nicht nur darin,
dass es Parabeln als Schnittkurven mit Ebenen zeigt, sondern auch dadurch, dass derartige Schnitte nie
Ellipsen sind. Wenn man ein hyperbolisches Paraboloid aber um unendlich ferne Punkte ergänzt, also den
affinen Raum der Koordinaten-Tripel x zu einem projektiven Raum der Koordinaten-Quadrupel ergänzt,
dann zeigt sich die projektive Gleichartigkeit. Die hinzugefügten Punkte sind die Punkte auf den beiden
unendlich fernen Geraden, in denen die Symmetrie-Ebenen von QH die unendlich ferne Ebene schneiden.
Diese Geraden sind Tangenten von QH im unendlich fernen Punkt auf der Symmetrie-Achse. Anders als
beim einschaligen Hyperboloid ist die unendlich ferne Ebene des affinen Raums Tangenten-Ebene der
projektiven Erweiterung.

Bei der projektiven Betrachtung von QH gibt man die Unterscheidung von endlichen und unendlich fernen
Ebenen auf. Man kann eine beliebige Ebene E des projektiven Raums auszeichnen und die Menge der Punkte,
die nicht auf E liegen, als Punkte des zugehörigen affinen Raums ansehen. Wenn E keine Tangenten-Ebene ist,
erscheint QH in diesem affinen Raum als Hyperboloid. Die zugehörige Gleichung ergibt sich dann, indem man
die Koordinaten der ursprünglichen Gleichung des Paraboloid transformiert. Wenn man diese Transformation
an Koordinaten-Tripeln (statt Quadrupeln) durchführt , ist wesentlich, dass im Nenner der Formeln für die
Transformation Koordinaten-Variablen vorkommen. Wir zeigen diese Transformation am Beispiel der
Gleichung des hyperbolischen Paraboloids für das Standard-Viereck.

Die zu einem nicht komplanares Viereck ABCD bestimmte allgemeine Gleichung
(*)
der Quadrik QH wird bei Einsetzung der Quadrupel (1 ; 0 ; 0 ; 1), (1 ; 1 ; 1 ; 1),
(0 ; 1 ; 0 ; 1) und (1 ; 1 ; -1 ; 1) und tvk = 1 zur Gleichung
.
Die Ersetzung

ergibt dann die Gleichung .
Diese ist äquivalent mit der Gleichung , die man für tvk = 2 aus
(*) als Gleichung eines einschaligen Hyperboloids in dem Koordinaten-System erhält,
das zu den Koordinaten mit dem Querstrich gehört.