Es lebe die Geometrie!

Distanzfaktoren-Tripel

--> https://www.vivat-geo.de/Pdf-Dateien/Schwerpunktskoordinaten.pdf

In dieser Animation ist ein Distanzfaktor-Tripel zum Punkt (und zu ) auf dem
Umkreis des Dreiecks ABC, da für die signierten Abstände von die folgende Gleichung gilt:
. Wegen gilt Entsprechendes für .
Das Tripel ist das normierte Schwerpunktskoordinaten-Tripel des Punkte Q* auf
den Einheitskreis um das Inkreis-Zentrum von ABC. Dies bedeutet, dass bzw. bzw.
der Quotient aus den Inhalten der orientierten Dreiecksflächen BCQ* bzw. CAQ* bzw. ABQ* und
ABC ist. Der Trägerpunkt P von und ist mit dem Inkreis-Zentrum und dem Umkreispunkt Q
kollinear. P bzw. Q ist der bezüglich ABC isogonal konjugierten Punkt des unendlich fernen Punktes
auf der Geraden bzw. . Nach dem Satz von Ptolemäus ist (a ; b ; c) ein Distanzfaktor-
Tripel für alle Umkreis-Punkte P, wobei a, b und c die Seitenlängen von ABC sind. Da (a ; b ; c)
andererseits ein Schwerpunktskoordinaten-Tripel des Inkreis-Zentrums ist, sind die Koordinaten-
Tripel von allen Punkten der Geraden Distanzfaktor-Tripel von P.

Wenn der Vektor in Schwerpunktskoordinaten durch (r ; s ; t) gegeben ist, dann ist durch das
Matrixprodukt 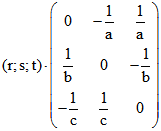ein Vektor in Richtung von bestimmt, der allerdings
eine andere Länge hat. Dabei sind a, b und c die Seitenlängen des Dreiecks ABC. Wenn die Vektoren
, und in einem zweidinesionalen kartesischen Koordinatensystem durch ,
und angegeben werden und durch (x;y), dann ergibt sich ein Vektor in Richtung von
aus .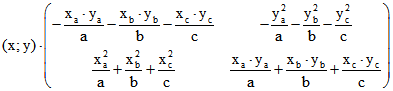

Die Tripel (1;1;1), (-1;1;1), (1;-1;1) und (1;1;-1) spielen eine besondere Rolle in der
Dreiecksgeometrie. Sie sind die Schwerpunktskoordinaten-Tripel der Punkte S, , und
, wobei S der Schwerpunkt des Dreiecks ABC ist und die antikomplementäre
Ergänzung, zu der A, B und C die Seitenmitten sind. Andererseits sind diese Tripel Distanzfaktor-
Tripel der Feuerbach-Punkte des Dreiecks . Dies sind die Berührpunkte der Berührkreise
von mit dem Umkreis von ABC. Die Zentren dieser Berührkreise sind die Nagel-Punkte
, , und von ABC. Diese vier Nagel-Punkte bilden eine orthozentrierte Vierpunkt-
Menge, bei der jeder der Punkte Höhenschnittpunkt des Dreiecks aus den drei übrigen Punkten ist.
In jedem dieser Dreiecke ist das Dreieck der Höhenfußpunkte. Die Streckung mit dem
Zentrum S und dem Faktor -0,5 bildet die vier Nagel-Punkte in die Berührkreis-Zentren von ABC
und in ABC selbst ab.
Die Animation zeigt die Bewegung des Träger-Punktes P auf dem Umkreis von ABC , die durch
den weißgefüllten Pfeil gesteuert wird, der sich mit der Spitze auf dem Einheitskreis um das Inkreis-
Zentrum von ABC dreht. Der magentafarbene Punkt Q* hat in jeder Stellung ein Schwerpunkts-
Koordinaten-Tripel, das Distanzfaktor-Tripel von P ist. Q* bewegt sich auf dem Umkreis, es sei
denn, dass die magentafarbene Gerade durch das Inkreis-Zentrum und Q* durch einen der Punkte
S, , oder geht. Dann bewegt sich Q* zu diesen Punkten hin und P bleibt an der Stelle
eines Feuerbach-Punktes von stehen. Dieser Punkt ist Berührpunkt des Umkreises von
mit dem Berührkreis um einen Nagel-Punkt, der auf der gelb gezeichneten Orthopolaren
von P liegt. Diese Orthopolare ist die Parallele zur Wallace-Geraden von P durch den Höhenschnitt=
punkt H von ABC. Sie ist stets senkrecht zu dem weißgefüllten Pfeil gerichtet.