Es lebe die Geometrie!

Koppelgetriebe

Bei einem Koppelgetriebe bewegen sich zwei Punkte A und B auf zwei Führungskreise so dass ihr
Abstand konstant bleibt. Die Strecke AB ist also eine Sehne konstanter Länge für das Kreispaar. In
der Getriebelehre wird die Sehne als 'Koppel' bezeichnet und die Verbindungsstrecken zwischen den
Zentren M1 und M2 der Kreise mit A und B als 'Arme'.

Die Animation simuliert Koppelgetriebe bei denen die Punkte A und B ihre Führungskreise ganz
durchlaufen, also darauf nicht nur hin- und her-schwingen. Es sind also Doppelkurbelgetriebe.
Die Drehpunkte M1 und M2 der beiden Arme haben den Abstand 0,6 und die Koppel AB hat
die Länge 1. In der ersten Periode sind beide Kreis-Radien gleich 1, in der zweiten 1 und 1,32.
Die dunkelblaue Kurve ist die Enveloppe der Sehnengeraden, die hellblaue ist die Polkurve und
die grüne die Momentanpolkurve. Ihr Zusammenhang ergibt sich durch die Geschwindigkeitspfeile.
Dabei sind die weiß gefüllten Pfeile gleich lang, da die Sehnenlänge sich nicht ändert.

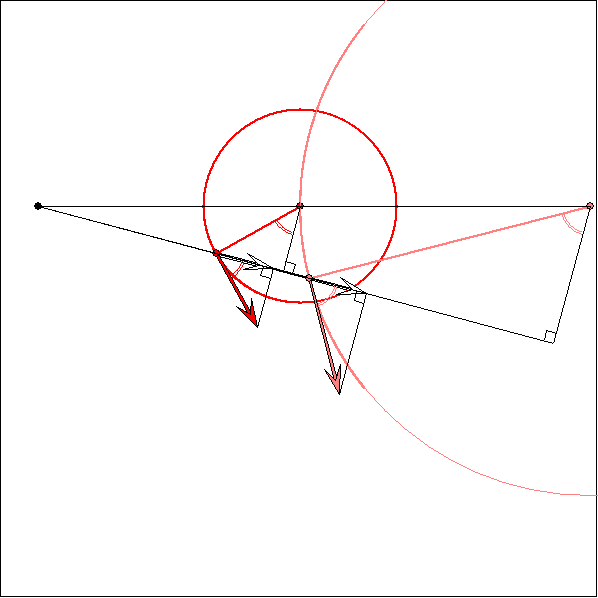
Die beiden Bilder der Gleitschau sollen die Zusammenhänge zwischen Geschwindigkeiten,
Längen und Winkeln bei einem Koppelgetriebe erläutern. M1 und M2 sind die Zentren der
beiden Führungskreise für die Sehne AB mit konstanter Länge, die hier die Koppel darstellt.

Bild 1 : Für den schwarzen Schnittpunkt Z der Geraden M1M2 und AB gilt: Das Verhältnis der
Winkelgeschwindigkeiten und der Punkte A und B auf ihren Kreisbahnen stimmt stets mit
dem Verhältnis der Streckenlängen und überein.

Begründung: Die Radien der beiden Führungskreise seien und genannt und die Größen der
rot markierten Winkel bei M1 und M2 mit und . Der dunkel- bzw. hell-rot markierten Winkel
bei A bzw. B hat die gleiche Größe. Für die Geschwindigkeiten und der Punkte A und B
gilt darum , denn die weiß gefüllten Geschwindigkeits-Vektoren sind die
Komponenten von und in Richtung der Sehne und diese sind gleich lang, da sich die Sehnenlänge
nicht ändert. Für die Längen bzw. der Lote von M2 bzw. M1 auf die Gerade AB gilt darum
, Nach dem Strahlensatz folgt daraus .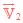

Bild 2 : An den Momentanpol D ist ein dunkel- bzw. hell-roter Geschwindigkeitsvektor bzw.
angeheftet, der angibt, wie schnell der Punkt D wäre, wenn er sich mit der Geraden AM1 bzw.
BM2 so bewegen würde, dass dabei der Abstand von M1 bzw. M2 unverändert bleibt. Die Spitzen
der beiden dunkel-roten bzw. hell-roten Pfeile liegen also auf einer Geraden durch M1 bzw. M2.
Die tatsächliche Bewegung wird aber durch den grünen Vektor der 'Polwechselgeschwindigkeit'
beschrieben, der tangential zur grünen Momentanpol-Kurve verläuft. Dabei gilt:

1. Die Spitzen , und der Vektoren , und liegen auf dem Thales-Kreis über .
Dieser Kreis wird auch als 'Hartmann-Kreis' bezeichnet.
2. Die Geraden und DZ sind orthogonal.
3. Die Winkel und sind gleich groß.

Begründung zu 1 : Wenn man in eine Komponente senkrecht zur Geraden M1D und eine
Komponente zerlegt, dann bewirkt nur ein Veränderung der Richtung dieser Geraden. Die
Winkelgeschwindigkeit von A ist auch die Winkelgeschwindigkeit der Geraden M1D . Damit gilt
, da sich die Gerade um M1 dreht. Also liegt die Spitze von auf der
Senkrechten zu durch die Spitze dieses an D angehefteten Vektors. Entsprechend schließt man für
die hell-roten Geschwindigkeits-Vektoren. Darum ist die Spitze von der Schnittpunkt der beiden
Senkrechten zu den roten Vektoren durch deren Spitze. Folglich liegen diese Spitzen auf dem Hartmann-Kreis.

Begründung zu 2 :

Es sei die Größe des Winkels M1DZ, die des Winkels M2DZ. und die des Winkels DZM1.
Dann ist nach dem Sinus-Satz ,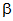
also .

Begründung zu 3 :

sei die Größe des gesuchten Winkels und die des Winkels . Dann ergeben die Winkel
mit der Spitze in D : . L sei der Fußpunkt des Lots von auf DZ.
Dann ist die Größe des Winkels gleich der von und nach dem Umfangswinkel-Satz auch
gleich . Dann zeigen die Winkel mit der Spitze in D : . Es folgt .

Die Animation simuliert ein Zwilligskurbelgetriebe. Die zwei Führungskurven der Sehne sind Kreise mit
dem Radius 1, deren Mittelpunkte M1 und M2 die Sehnenlänge als Abstand haben. Diese Mittelpunkte
bilden mit den Endpunkte A und B der Sehne ein Antiparallelogramm, da sich zwei gegenüberliegende
Seiten kreuzen.

In der ersten Periode der Animation ist die Sehnenlänge 0,6, also kleiner als der Kreis-Radius 1.
Das Getriebe wird dann 'gleichläufig' genannt, da A und B gleichsinnig rotieren. In dem Fall ist
der Momentanpol D Schnittpunkt im Innern der Arme und liegt auf der Symmetrieachse des
Anti-Parallelogramms. Die Summe der Abstände des Momentanpols D von M1 und M2 ist
darum gleich der Armlänge. Da diese konstant ist, bewegt sich D auf einer Ellipse mit den Kreis-
Zentren als Brennpunkte. Die Symmetrieachse des Antiparallelogramms ist die Tangente in D.

In der zweiten Periode ist die violette Spur der Sehnen-Mitte hinzugefügt. Eine derartige Spur heißt
'Koppelkurve'. Es ist die Spur eines Punktes P, der fest mit der Sehne verbunden ist, so dass bei der
Bewegung der Sehne das Dreieck ABP in ein gleich orientiertes kongruentes Dreieck A'B'P' übergeht.
Für die Sehnen-Mitte ist die Spur eine 'boothsche Lemniskate'. Sie ergibt sich auch durch Spiegelung
der Mitte Z von M1 M2 an den Tangenten der hellgrünen Momentanpol-Kurve. Wenn man die Punkte
der Koppel-Kurve an dem Kreis um die Mitte von M1 M2 mit dem Radius 0,7 spiegelt, entsteht die
dunkelgrüne Ellipse, deren Nebenachse mit der Hauptachse der Momentanpol-Kurve zusammenfällt.
Ihre Halb-Achsen sind proportional zu den Kehrwerten von den Halb-Achsen der hellgrünen Ellipse.

In der dritten Periode der Animation beträgt die Sehnenlänge s =, ist also größer als der Kreis-
Radius. Das Getriebe heißt dann 'gegenläufig', weil sich A und B entgegengesetzt auf ihren Kreisen
bewegen. Der Momentanpol D liegt auf der Verlängerung der Arme und auf der Symmentrieachse
des Antiparallelogramms. Da D außerhalb der Arme liegt, ist hier nicht die Summe der Abstände
von M1 und M2 konstant, sondern die Differenz. Diese stimmt auch hier mit dem Radius der beiden
Führungskurven überein. Darum ist die Momentanpol-Kurve eine Hyperbel, die M1 und M2 als
Brennpunkte hat, und zwar wegen der Sehnenlänge eine gleichseitige Hyperbel. Die Spur der
Sehnen-Mitte P ist eine Lemniskate im üblichen Sinne mit M1 und M2 als Lemniskate-Brennpunkten.
Für alle Punkte der Lemniskate ist also das Produkt der Abstände von den beiden Brennpunkten
gleich, nämlich hier 0,5.

Das ergibt sich folgendermaßen : A sei der Punkt . Dann ist B Schnittpunkt der
Kreise und . Für die in der Animation
dargestellten Fälle ergibt sich 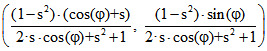als Lösung des Systems
dieser Gleichungen. Die Mitte P der Sehne AB ist dann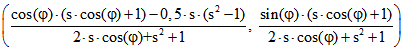
.

Das Produkt der Abstände dieses Punktes von M1 und M2 ist für s = konstant, nämlich gleich
dem Quadrat des halben Abstands der Mittelpunkte, also gleich 0,5. Für beliebiges s ergibt sich durch
Spiegelung an dem Kreis mit dem Radius um die Mitte Z von M1M2 aus P der Punkt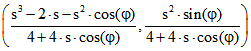
. Er liegt für s > 1 auf der
Hyperbel mit dem Mittelpunkt in Z und den Halbachsen und .
Im Sonderfall s = ist dies die hellgrüne Kurve der Momentanpole. Für s < 1 ist das
Kreisspiegelungs-Bild der boothschen Lemniskate eine Ellipse mit den Halbachsen und .

Die vierte Periode der Animation verdeutlicht, wie die Hyperbel durch Spiegelung an dem schwarzen Kreis
um Z entsteht. Die fünfte Periode zeigt die blaugrüne Evolute der violetten Koppel-Kurve. Die Evolute ist
Kurve der Krümmungs-Mittelpunkte der Koppel-Kurve. Diese sind stets kollinear mit dem Koppel-Punkt
P und dem Momentanpol D.

In der Gleitschau werden nach der Animation Standbilder daraus gezeigt. Das letzte Bild verdeutlicht, wie ein
Krümmungs-Mittelpunkt der Koppel-Kurve mit dem Koppel-Punkt P konstruiert wird. Dazu wurden die
Geschwindigkeits-Vektoren von A, B, D und P hinzugefügt und die Ergänzungen im Hartmann-Kreis. Der
Krümmungs-Mittelpunkt zu P ist der Schnitt-Punkt der Geraden durch die Spitzen der blau-violetten Pfeile
und der Geraden durch P und D.

Die Animation zeigt eine gleichschenklige Schwingkurbel. Dabei hat ein Arm die Länge s der Koppel
und der andere ist so lang wie der Abstand a der beiden Mitten M1 und M2 der kreisförmigen
Führungskurven. M1, M2 und die Endpunkte B und A der Kurbel bilden also ein Drachen-Viereck.
In beiden Teilen der Animation stimmt die Länge des Arms an M1 mit der Länge 1 der Koppel überein.
Der Abstand von M1 und M2 ist im ersten Teil gleich 2 und im zweiten 0,5; in beiden Teilen ist die Länge
des Arms an M2 so groß wie der Abstand von M1 und M2.

Die hellgrüne Kurve der Momentan-Pole ergibt sich auch hier durch die Schnitt-Punkte der Geraden M1A
und M2B . Sie ist eine 'pascalsche Schnecke', benannt nach dem Vater von Blaise Pascal (1623-1662).
Die pascalsche Schnecke wird definiert als geometrischer Ort der Fußpunkte der Lote von einem Punkt M
auf die Tangenten eines Kreises K. Wenn M der Mittelpunkt von K ist, liegen die Fußpunkte auf K und wenn
M auf dem Rand von K liegt, ist es eine Kardioide (Herz-Kurve) mit der Spitze in M. Für M im Innern von K
ist die pascalsche Schnecke eine einfach geschlossene Kurve, für M außerhalb von K ergibt sich eine Schleife
mit M als Doppel-Punkt. In der Animation ist M gleich M1 und der K der schwarze Kreis mit zwei Berühr-
Punkten mit der hellgrünen pascalschen Schnecke

Neben dieser Erzeugung der pascalschen Schnecke als Fußpunkt-Kurve stellt die Animation noch drei weitere
Methoden dar. Sie entsteht nämlich durch Spiegelung an dem blauen Kreis aus dem dunkelgrünen Kegelschnitt,
der im ersten Teil der Animation eine Ellipse und im zweiten Teil eine Hyperbel ist. Außerdem ist sie eine
Konchoide, die durch folgende Eigenschaft definiert ist: Es gibt einen Punkt N und einen Kreis L durch N
derart, dass für jede Gerade g durch N ihr zweiter Schnittpunkt mit L in der Mitte von zwei Schnittpunkten
mit der pascalschen Schnecke liegt. In der Animation ist N gleich M1 und L der blaue Kreis. L wird als
Konchoiden-Leit-Kurve bezeichnet und N als Konchoiden-Pol. Die Animation zeigt, dass die Konchoide
auch als Spur einer Überlagerung zweier gleichförmiger Kreisbewegungen dargestellt werden kann. Dabei
rollt der schwarze Gang-Kreis ohne zu Rutschen an dem gleich großen Rast-Kreis ab mit dem gelben Punkt
G als Berühr-Punkt. Die Konchoide ist dann die Spur des Punktes D an der Spitze des kleinen Pfeils, der sich
doppelt so schnell dreht wie der Radius-Vektor des Rast-Kreises. Eine derartige Überlagerung zweier
gleichförmiger Kreis-Bewegungen wurde von Nikolaus Kopernikus (1473-1543) für sein Modell der Planeten-
Bewegung benutzt (siehe die Seite Kopernikus-Modell).

Die Begründung für die geometrischen Zusammenhänge dieser fünf Erzeugungs-Methoden folgt an Hand der
Zeichnungen in der nächsten Gleitschau.

Die Gleitschau zeigt wieder eine gleichschenklige Schwingkurbel, bei der also die Strecke M1M2 mit
den beiden Armen und der Koppel einen Drachen bilden. Das Verhältnis des Abstands d von M1
und M2 zu der Koppel-Länge s ist in den Bildern 1 bis 4 gleich 2 und bei Bild 5 gleich 1,15.

Das erste Bild zeigt mit Hilfe der Pfeile, dass sich die grüne Momentalpol-Kurve als Überlagerung zweier
gleichförmiger Kreisbewegungen darstellen lässt, wobei der kleinere Pfeil doppelt so schnell rotiert wie der
größere. Die dadurch entstehende pascalsche Schnecke ist die Spur eines Punktes auf einem 'Gang-Kreis'
mit dem Radius r, der ohne zu Rutschen an einem gleich großen 'Rast-Kreis' abrollt. (Ein Punkt auf dem
Rand des Gang-Kreise würde eine Kardioide als Spur haben.)

Der gelbe Mittelpunkt G des langen Pfeils ist der Schnittpunkt der Symmetrie-Achse g des Drachens mit
der Geraden, die mit dem Arm AM1 einen gleich großen (rot markierten) Winkel einschließt wie die
Gerade M1M2 mit g. Der graue Drehpunkt H des langen Pfeils ist der Schnittpunkt von M1M2 mit
der Parallelen zu AM1 durch G. Dann sind die Dreiecke M1M2A, HM2G und HGM1 zueinander
ähnlich. Mit dem Abstand b von H und M1 errechnet man daraus
, also und ,
folglich und .
Da s und d bei der Bewegung der Koppel konstant sind, gilt dies auch für r, so dass der gelbe Punkt
G tatsächlich auf einem Kreis umläuft.

Wenn die Größe des rot markierten Winkels GM2M1 bei M2 mit bezeichnet wird und die des
schwarz markierten Winkels M2M1G bei M1 mit , dann erweist sich die Größe der grün markierten
Winkel bei G und beim grünen Momentanpol D als gleich, nämlich als . Darum liegt der
Momentanpol D auf dem hellgrünen Kreis um G durch M1 und B. Wenn also der lange Pfeil die Länge
2r hat, der kurze die Länge b und beide den Winkel einschließen, dann liegt der Momentanpol D
an der Spitze des kleinen Pfeils. Da M1 im Koordinaten-Ursprung liegt, ist der Ortsvektor von D durch

oder
in komplexer Form durch gegeben. Die Bewegung bei mit der Zeit linear
wachsendem ist eine Überlagerung zweier gleichförmiger Kreis-Bewegungen zur Funktion
.

Der Rastkreis geht durch die beiden Schnittpunkte der roten Führungskreise. Er ist darum der eindeutig
bestimmte Kreis im Kreisbüschel, das von den beiden Führungskreisen erzeugt wird, der sich durch
eine nicht-triviale Streckung mit dem Zentrum M2 aus dem Führungskreis um M1 ergibt.

Die Ableitung von ergibt
, wobei die Richtung
senkrecht zum Radius-Vektor des hellgrünen Kreises um G gerichtet ist. Darum berührt dieser
die Momentanpol-Kurve in D.

In Bild 2 der Gleitschau wurden die beiden Pfeile in Bild 1 durch zwei weitere zu einem Parallelogramm
ergänzt. Dadurch wird klar, dass die pascalsche Schnecke eine Konchoide ist mit einem Kreis vom Radius
r als Leitkurve und A als Konchoiden-Pol, der auf dem Kreis liegt. Die Strecke AD schneidet den Kreis
im Anfangspunkt R des hinzugekommenden kurzen Pfeils. Dass es sich bei der Momentanpol-Kurve um
eine Konchoide handelt, folgt daraus, dass die Länge der Strecke RD für alle Punkte der Kurve gleich ist,
insbesondere auch für den Punkt, der durch Spiegelung von D an R entsteht.

In Bild 3 kommt der Kreis k hinzu, der die Scheitelpunkte der pascalschen Schnecke auf der Rechtsache
als Endpunkte eines Durchmessers hat und den Spiegelungs-Punkt J von M1 an H als Mittelpunkt. Die
Fußpunkte der Lote von A auf die Tangenten von k liegen alle auf der pascalschen Schnecke und die
Fußpunkte der Lote auf die Normalen von k auf dem Konchoiden-Leitkreis, da die Strecke JR orthogonal
zu ist. Der Radius von k stimmt darum mit der Länge des langen Pfeils überein. Bild 4 zeigt, wie
man an der pascalschen Schnecke erkennt, wie lang der kurze Pfeil ist, dessen Länge mit dem Radius
des Leitkreises übereinstimmt.

Die Umformung für den
Term der Momentanpol-Kurve zeigt, dass das Bild dieser pascalschen Schnecke bei Spiegelung an dem
Kreis k um M1 mit dem Radius 2b ein Kegelschnitt ist, denn aus dem Punkt
ergibt sich bei der Spiegelung der Punkt 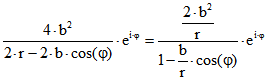, der auf dem
Kegelschnitt mit dem Halbprameter und der numerischen Exzentrizität liegt. Die Brennpunkte
des Kegelschnitts sind dabei der Punkt M1 und Bild von M2 bei Spiegelung an k.

In Bild 5 wurde zu der hellgrünen Momentanpol-Kurve deren Bild bei der Spiegelung an dem braunen
Kreis k gezeichnet. Es ist die dunkelgrüne Ellipse. Die schwarz markierten Winkel bei A sind darum
gleich groß. Sie stimmen mit der Größe der schwarz markierten Winkel beim Momentanpol überein, weil
Winkelgrößen bei Kreisspiegelungen unverändert bleiben. Aus diesem Grund sind auch die grün markierten
Winkel bei A und beim Momentanpol D gleich groß. Der magentafarbene Kreis durch M1, M2 und D
wir in die gleichfarbige Gerade durch das Spiegelbild von D und das von M2 gespiegelt, das der
rechten Brennpunkt der Ellipse ist. Der linke Brennpunkt ist M1, da die Gerade M1D bei der Spiegelung
fest bleibt.