Es lebe die Geometrie!

Der Wendekreis bei der Koppelkurve

Eine Koppelkurve K(Q) ist die Spur eines Punktes Q mit festem Abstand von den Endpunkten A und B
einer Sehne konstanter Länge, die in einer Ebene bewegt wird. Dabei ist im klassischen Fall die Sehne
die Koppel eines Koppelgetriebes, bei dem A und B auf zwei Kreisen geführt werden. Die Evolute von
K(Q) ist der geometrische Ort der Krümmungs-Mittelpunkte zu den Punkten von K(Q). Der zu einem
Koppel-Punkt P der Koppelkurve gehörige Krümmungs-Mittelpunkt P* ergibt sich näherungsweise
zum Beispiel dadurch, dass man benachbarte Punkte R und S auf der Kurve vor bzw. nach P wählt
und den Schnittpunkt der Mittelsenkrechten von RP und PS bestimmt. Den exakten Wert für P*
erhält man durch den Grenzübergang R --> P und S --> P. Wenn bei diesem Grenzübergang der
Schnitt-Punkt ins Unendliche rückt, hat K(Q) bei P einen Scheitel- oder Wende-Punkt, die
Krümmung ist Null und der Krümmungs-Radius ist unendlich.

Der Krümmungs-Mittelpunkt P* liegt stets auf der Geraden durch P und den Momentan-Pol D. Dies gilt
insbesondere auch für den Punkt Q, den wir zur Definition der Koppelkurve K(Q) benutzen. Zu jeder
Stellung der Koppel kann ein 'Wendekreis' definiert werden, mit dem bestimmt werden kann, wo Q* auf
dieser Geraden liegt. Das soll mit Hilfe der folgenden Animation erklärt werden.

In der Animation werden Koppelkurven eines Zwillingskurbel-Getriebes mit den Armlängen 1 und mit
blau-violett und zum Teil ihre Evolute (blau-grün) dargestellt. Dabei bleibt die
Stellung der Koppel AB unverändert, nicht aber der Koppelpunkt Q, dessen Spur bei der (nicht gezeigten)
Bewegung von A auf seinem Kreis um M1 die jeweils gezeigte Koppelkurve K(Q) ist.

Im ersten Bild der Animation ist Q der Mittelpunkt der Koppel AB . K(Q) ist dann die blau-violette Lemniskate.
Q und der zugehörige Krümmungs-Mittelpunkt Q* der Koppel-Kurve ist durch eine Gerade g mit dem
Momentanpol D verbunden. Auf g liegt außerdem der weiß gefüllt dargestellte Punkt S auf dem schwarzen
'Wendekreis', der wie die Koppel unverändert bleibt und die hellgrüne Momentanpol-Kurve in D berührt.
Die vier kollinearen Punkte Q, D, Q* und S stehen in einer besonderen Beziehung zueinander, die durch den
Satz von Euler-Savary ausgedrückt wird
(Leonhard Euler 1707-1783; Félix Savary 1797-1841):

S ist das Bild der Spiegelung von Q* an dem Kreis um Q durch D.

Es gilt also . Dabei liegen Q* und S auf g stets auf der gleichen Seite von Q.

Falls die vier Punkte auf g die Reihenfolge D Q Q* S haben, ist äquivalent
mit , also mit ,
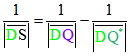was wiederum gleichwertig mit und ist.
Bei anderen Lagen der Punkte ergibt sich eine entsprechende Gleichung mit eventuell anderen
Vorzeichen. Wenn man auf g eine Orientierung festlegt und dazu eine signierte Streckenlänge
benutzt, die z. B. für Punkte X auf g rechts von D ein Plus-Zeichen setzt und für die links von D ein
Minus-Zeichen, dann gilt für alle Lagen der Punkte die Gleichung .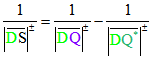

In der Animation wird Q zunächst auf der Koppel bis zum Endpunkt A verschoben. Dann fällt K(Q)
mit dem roten Führungs-Kreis um M1 zusammen und Q* ist gleich M1. In der zweiten Periode wandert
Q auf der Koppel bis B. Dann ist K(Q) der hell-roten Führungs-Kreis um M2 und Q* gleich M2. In der
dritten Periode geht Q zurück bis zur Koppel-Mitte. Bei diesen Bewegungen ändert sich die grün-blaue
Evolute mit der Koppelkurve, während der Momentan-Pol D und der Wendekreis unverändert bleiben.
Auch die durch den grünen Pfeil an D dargestellte Polwechsel-Geschwindigkeit bleibt unverändert.
gibt die Geschwindigkeit von D bei der Bewegung auf der hellgrünen Momentanpol-Kurve an
und ist darum auch tangential zum Wendekreis gerichtet. Der Thales-Kreis über schneidet den
Wendekreis orthogonal. Er wird Hartmann-Kreis genannt (siehe dazu die Seite ' Koppelgetriebe').

Zu Beginn der vierten Periode der Animation werden die Geschwindigkeits-Vektoren von A, B und Q
eingezeichnet. Nach dem Satz von Ludwig Burmester (1840-1927) teilt die Spitze von die Strecke von
der Spitze von zur Spitze von im gleichen Verhältnis wie Q die Strecke AB teilt. Im Momentanpol
D ist der zugehörige Geschwindigkeitsvektor angeheftet, der die Geschwindigkeit des Punktes D
angibt, wenn er sich nicht auf der Geraden DQ verschieben würde, sondern nur auf Grund der momentanen
Drehung dieser Geraden um Q* bewegen würde. ist die Komponente der Polwechselgeschwindigkeit
senkrecht zu DQ, so dass und ein rechtwinkliges Dreieck aufspannen, dessen zweite Kathete
parallel zu DQ ist.(Vergleiche dazu auch die Erklärungen auf der Seite 'Koppelgetriebe'.) Entsprechendes
gilt für die Komponente von senkrecht zu DA bzw. DB. Da der Momentanpol D momentanes Drehzentrum
der Koppel ist, gilt für die Winkelgeschwindigkeit der Koppel: . Für den Term
auf der rechten Seite der Gleichung von Euler-Savary ergibt sich nun mit dem violett markierten Winkel
zwischen der Geraden DQ und dem Vektor nach dem Strahlensatz: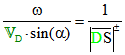
.
Der Wendekreis kann nun folgendermaßen definiert werden: Es ist der Kreis mit dem Durchmesser ,
der den Vektor in D berührt, und zwar je nach Vorzeichen von rechts oder links davon. Dabei ist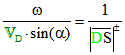
, und dieser Kreis hängt nur von der Stellung der Koppel ab, aber nicht von der
speziellen Wahl des Koppelpunktes.

Im Lauf der vierten Periode der Animation wird Q auf der Lemniskate herumgeführt. Dann liegt die Spitze von
nicht mehr auf der Geraden durch die Spitzen von und , aber das durch diese Spitzen gebildete
Dreieck ist nach dem Satz von Burmester gleichsinnig ähnlich zum Dreieck ABQ.

Da für Q = A bzw. Q = B der Krümmungs-Mittelpunkt M1 bzw. M2 ist, folgt aus dem Satz von Euler-Savary,
dass der Wendekreis der Kreis durch folgende drei Punkte ist:

D,
Bild von M2 bei Spiegelung am Kreis um B durch D,
Bild von M1 bei Spiegelung am Kreis um A durch D.

Die Animation begründet den Begriff 'Wendekreis'. Hier wurden als Koppelpunkte die Punkte Q des
schwarzen Wendereises gewählt. Dann ist die Krümmung der zugehörigen Koppelkurve in Q gleich Null,
falls S ungleich D ist. Denn die Gerade g durch D und Q hat keinen weiteren gemeinsamen Punkt mit dem
Wendekreis. Darum stimmt S mit Q überein. Da S das Bild von Q* bei Spiegelung an dem Kreis um Q
durch D ist, muss Q* der unendlich ferne Punkt auf g sein. Folglich ist der Krümmungsradius unendlich
und die Krümmung Null. Diese Punkte mit der Krümmung Null können Scheitelpunkte oder Wendepunkte
der Koppelkurve sein. Zumeist sind sie Wendepunkte.

Die Animation zeigt die violette Koppelkurve bei einem Koppelgetriebe mit den Armlängen 1, dem
Abstand 2 der Mittelpunkte M1 und M2 und der Länge 1 der Sehne AB. In der ersten Periode der
Animation bildet der Koppelpunkt Q mit A und B ein gleichseitiges Dreieck. Die Koppelkurve besteht
aus zwei getrennten Teilen, die näherungsweise Abschnitte des Randes eines gleichseitigen Dreiecks mit
der Seitenlänge 2 bilden. Die Vervollständigung dieses Randes ergibt sich durch den entsprechenden
Koppelpunkt Q' auf der zu AB gehörenden Rückwärts-Sehne AB'. In der zweiten Periode wird Q auf
der Mittelsenkrechten von AB verschoben.

Bild 1 der auf die Animation folgenden Gleitschau zeigt die blaugrüne Evolute der Koppelkurve mit
einem Wendekreis. In den Bildern 2 bis 6 wurden die Wendekreise zu Stellungen der Koppel
gezeichnet, in denen der Koppelpunkt Q den Wendekreis trifft, so dass die Koppelkurve hier die
Krümmung Null hat und der zugehörige Punkt der Evolute im Unendlichen liegt. Diese Punkte sind
rot markiert. In den Bildern 7 bis 11 ist die hellgrüne Rastpol-Kurve der Momentanpole zusammen
mit der zugehörigen dunkelgrünen Gangpol-Kurve mit verschiedenen Berührpunkten dargestellt.
Bild 12 zeigt die blaue Enveloppe der Ko-Sehne BB', und Bild 13 die Koppelkurve für den Fall,
dass Q der Mittelpunkt von AB ist, zusammen mit der Momentanpol-Kurve und der Rauten-
Ergänzung der Sehnen.