Es lebe die Geometrie!

Inversion und Anti-Inversion beim Kreis

Unter 'Inversion' verstehen wir hier die Spiegelung an einem Kreis K und unter 'Anti-Inversion' die
Verkettung der Spiegelung an K mit der Spiegelung an dem Mittelpunkt M von K. Gespiegelt werden
dabei zunächst geometrische Objekte wie Punkte, Geraden und Kreise in der Ebene, in der K liegt.
Der Definitionsbereich wird aber im Folgenden auf den dreidimensionalen Raum erweitert.

Ein Punkt P in der Ebene von K hat das Bild P ' bei Inversion oder Anti-Inversion an K auf der Geraden
durch P und das Zentrum M von K, so dass das Produkt der Abstände P von M und P ' von M mit den
Quadrat des Radius R von K übereinstimmt. Wenn dabei M zwischen P und P ' liegt, ist P ' Anti-Inversions-
Bild, andernfalls ist P ' Inversions-Bild von P. Für die Verschiebungs-Vektoren und ist das
Skalarprodukt also bei der Inversion gleich und bei der Anti-Inversion gleich . Die Bilder
von Geraden oder Kreisen in der Ebene von K ergeben sich dann daraus, dass man sie als Punktmengen
betrachtet. Bei Spiegelung an K ist das Bild eines Kreises L ebenfalls ein Kreis, falls M nicht auf L liegt,
andernfalls ist das Bild eine Gerade.

g sei die Gerade durch M und das Zentrum N des Kreises L. P und Q seien die Schnitt-Punkte von g mit L.
Wir denken uns auf g eine lokale Koordinaten-Achse gelegt, die bei M den Null-Punkt hat, und bezeichnen
die Koordinaten der Punkte auf g mit den zugehörigen kleinen Buchstaben. Der Mittelpunkt N der Strecke PQ
hat dann die Koordinate n = (p + q)/2. Der Mittelpunkt N' von P'Q', ist im Allgemeinen nicht das -Bild von N.
Seine Koordinate ist . Im Fall p > q ist r = (p - q)/2 der Radius von
L und der Radius vom -Bild von L. Der Faktor wirkt
hier wie der Streckungs-Faktor einer zentrischen Streckung mit Zentrum im Mittelpunkt des Kreises, an dem
gespiegelt wird. Dabei ist der Nenner die Potenz von M bezüglich L, also das Quadrat des Abstands
zwischen M und dem Berührpunkt einer Tangente an L durch M.

Die Ausweitung des Definitionsbereichs auf den dreidimensionalen Raum soll in der folgenden Animation
dargestellt werden. Wir orientieren uns dabei an dem Buch 'Circles' von Dan Pedoe.

Das erste Bild der Animation zeigt das Zentralprojektions-Bild des Paraboloids Par mit der Gleichung
und von dick gezeichneten Kreisen in der x-y-Ebene zusammen mit dünn gezeichneten
Ellipsen auf Par, die durch Projektion parallel zur z-Achse aus den Kreisen entstehen. Dabei wird der rote
Kreis KA mit dem Zentum A an dem grünen Kreis mit dem Zentrum in den Kreis KC um C
gespiegelt. Auf KA liegt ein Punkt P mit den Spiegelbild Q auf KC. Beide Punkte sind durch einen weißen
Ring markiert. Sie sind Berühr-Punkte des Kreises KM um M. Dabei ist M der Schnittpunkt der Geraden
PA und QC. Alle diese Punkte in der x-y-Ebene sind mit ihren Bildern bei Projektion parallel zur z-Achse
durch eine schwarze Strecke verbunden. Diese Bilder sind in gleicher Farbe gezeichnet und bei den Kreis-
Zentren etwas größer. Auf den Geraden durch die schwarzen Strecken ist für die Kreis-Zentren ein weißer
Punkt markiert, der für C den zughörigen Punkt auf Par verdeckt, aber mit diesem nicht zusammenfällt. Wir
bezeichnen ihn als den 'zum Kreis gehörigen Raum-Punkt'. Wenn das Kreis-Zentrum die Koordinaten (x ; y)
hat und der Radius des Kreises r ist, dann hat der Raumpunkt die Koordinaten .
Der Abstand vom Schnittpunkt der Geraden parallel zur z-Achse mit Par durch das Kreis-Zentrum also .

Die Bilder ParP und ParQ von P und Q bei der Projektion auf Par parallel zur z-Achse sind kollinear mit dem
Raumpunkt zu .

RA ist der Mittelpunkt der Ellipse, die aus KA durch Projektion parallel zur z-Achse auf Par entsteht.

Für den Kreis KA ist außer dem zugeordneten Raum-Punkt RA noch ein weiterer weißer Punkt im gleichen
Abstand vom Paraboloid-Punkt ParA auf der Parallelen zur z-Achse eingezeichnet, den wir Anti-RA nennen.
Er hat also die Koordinaten und liegt oberhalb von Par, während RA unterhalb Par liegt.
Die Auflösung der Gleichung nach r ergibt nur für eine reelle Zahl ,
nämlich , andernfalls ist das Ergebnis die rein imaginäre Zahl . Wir denken uns
darum jeden Kreis in der x-y-Ebene mit positivem Radius r von einem 'imaginären' Kreis überlagert, dessen
Radius ist. Beide Kreise haben die gleiche Form und Lage. Für den imaginären Kreis benutzen wir eine
aufgehellte Farbe gegenüber dem Zwillings-Kreis. Auf diese Weise erreichen wir, dass jedem Raumpunkt ein
Kreis in der x-y-Ebene eindeutig zugeordnet ist. Für die Punkte von Par sind es die Null-Kreise mit Radius Null,
die wir in der x-y-Ebene mit den Punkten (x;y) identifizieren.

Den zum imaginären Kreis KA zugehörigen reellen Kreis bezeichnen wir mit KA in dunklem Rot und analog
Anti-RA mit RA. Für jeden Punkt P der Ellipse, die aus KA durch Projektion parallel zur z-Achse auf Par
entsteht, inzidiert die Tangential-Ebene an Par in P mit RA. RA wird darum 'Pol' der Ebenen genannt, in der
die Ellipse liegt. Die Gerade durch RA und RM berührt Par in ParP.

Die Raum-Punkte RA zum reellen Kreis KA und RC zum reellen Kreis KC sind wie ParP und ParQ bei
Inverion am reellen Kreis kollinear mit dem Raumpunkt zu . Wenn RA das Koordinaten-Tripel
hat und das Tripel , dann teilt RC die Strecke von nach RA im
Verhältnis . Dabei ist der Nenner das Quadrat des Radius von .
Wenn man KA durch den zugehörigen imaginären Kreism KA ersetzt, aber unverändert lässt, dann
teilt RC die Strecke von nach RA im Verhältnis .


Das erste Bild der Animation zeigt, dass sich der Raum-Punkt des Berühr-Kreises KM als Schnittpunkt der
Raum-Geraden durch ParP und Anti-RA und der durch ParQ und RC ergibt. Der erste Teil der Animation zeigt
einen Umlauf von P auf KA . Dann wird der Augenpunkt der Zentral-Projektion in die x-y-Ebene verschoben
und anschließend in die z-Achse für eine unverzerrte Sicht auf die Kreise mit einem weiteren Umlauf. Dabei
werden die Abstände P von und Q von angezeigt, deren Produkt stets mit dem Quadrat des Radius
von übereinstimmt. Im letzten Teil der Animation wird der Raum-Punkt in Anti- verschoben.
Dabei verschiebt sich das Inversions-Bild KC von KA in das Bild bei der Anti-Inversion am imaginären
Kreis .

Die Raum-Punkte RA zum reellen Kreis KA und RC zum reellen Kreis KC sind ebenso wie ParP und ParQ
bei Anti-Inverion am imaginären Kreis kollinear mit dem Raumpunkt zu . Dabei berechnet man
das Teilverhältnis analog wie bei der Inversion, indem man durch das Tripel
des Raumpunkts vom Anti-Inversions-Kreis ersetzt.

Die Bilder bei der Inversion und bei der Anti-Inversion unterscheiden sich in folgender Hinsicht:

Der Kreis, an dem gespiegelt wird, ist bei der Inversion reell und bei der Anti-Inversion imaginär.
Sein Zentrum ist bei der Inversion äußerer Ähnlichkeits-Punkt und bei der Anti-Inversion innerer.
(Dabei heißt eine Punkt Ähnlichkeits-Punkt von KA und KC, wenn es durch ihn zwei gemeinsame
Tangenten an KA und KC gibt.) Im zweiten Fall teilt das Zentrum die Strecke AC im positiven
Verhältnis liegt also zwischen A und C, im ersten Fall nicht, denn das Verhältnis ist .
Bei der Anti-Inversion schneidet der Kreis, an dem gespiegelt wird, jeden Berühr-Kreis von KA
und KC, für den KA und KC auf verschiedenen Seiten liegen, in einem Durchmesser; bei der
Inversion schneidet er jeden Kreis senkrecht, für den KA und KC auf der gleichen Seite liegen.

Die Potenz des Zentrums des Kreises, an dem gespiegelt wird; ist aber bei der Inversion und der
Anti-Inversion bezüglich aller Berühr-Kreise gleich. Bei der Inversion ist diese Potenz das Quadrat
vom Radius des Inversions-Kreises, bei der Anti-Inversion muss man diesen Wert mit -1 multiplizieren.

Diese Animation stellt den räumlichen Zusammenhang zwischen einem Kreis um A, einem Kreis um ,
an dem gespiegelt wird, und dem Kreis um C als Spiegel-Bild übersichtlicher dar. Im ersten der vier Teile
wird die z-Koordinate des Raumpunktes RA zum Kreis KA verkleinert, so dass der Radius von KA sich
von 1 auf i verändert, wobei konstant bleibt und der Radius von KC erst vom 3,5 auf Null sinkt,
dann aber wieder auf 3,5 steigt. In der ersten Hälfte dieses Vorgangs sind und RC mit RA kollinear,
in der zweiten aber mit Anti-RA. Diese Variation ist nötig, damit durch die Spiegelung am Inversions-Kreis
der weiß umrandete Punkt P auf KA weiterhin ein Spiegel-Bild Q auf KC hat. Q ist nämlich dadurch festgelegt,
dass die Bilder ParP und ParQ von P und Q bei Projektion auf das Paraboloid parallel zur z-Achse mit
kollinear sind.

Im zweiten Teil der Animation wird die z-Koordinate von bei konstantem RA verkleinert. Dabei
verkleinert sich der Radius von KC von 0,35 auf Null bis C den Punkt erreicht und wächst dann
wieder bis 0,35 an, wobei dann zum imaginären Anti-Inversions-Kreis wird. Im dritten Teil
vergrößert sich die z-Koordinate von RA bei konstanten bis der Radius den Ausgangs-Wert 1
errreicht. In der ersten Hälfte dieses Vorgangs sind und RC mit Anti-RA kollinear, dann wieder
mit RA, nachdem KA reell geworden ist. Im vierten Teil läuft der Prozess des dritten Teils umgekehrt ab.

In dieser Animation wird der Ablauf der vorherigen für vier Spiegelbilder gezeigt. Dabei wird der reelle
und der imaginäre Kreis um A bzw. A am reellen und am imaginären Kreis um bzw. gespiegelt.
Der Kreis um D bzw. D ist das Spiegelbild der Paarung reell-reell für Urbild-Kreis und Inversions-Kreis,
der um E bzw. E für die Paarung imaginär-reell, der um F bzw. F für die Paarung reell-imaginär und der
Kreis um G bzw. G für die Paarung imaginär-imaginär. Die letzten beiden Bilder ergeben sich aus den
ersten beiden durch Spiegelung am Punkt .

Die Animation zeigt die zwei Möglichkeiten, den roten Kreis KA in den dunkelblauen Kreis KC zu
spiegeln, nämlich mit dem dunkelgrünen Inversions-Kreis KÄaußen und den hellgrünen Anti-Inversions
-Kreis KÄinnen. Die beiden Ähnlichkeits-Punkte Äaußen und KÄinnen von A und C sind die beiden
Punkte auf der Geraden AC, die mit zwei gemeinsamen Tangenten von KA und KC inzidieren. Sie
sind Zentren von Streckungen, die KA in KC abbilden. Der hellblaue Kreis entsteht durch Spiegelung
des dunkelblauen am Punkt Äinnen und am Kreis Äaußen . Die weiß umrandeten Punkte P und Qa gehen
durch Inversion an KÄaußen auseinander hervor und die Punkte P und Qi durch Anti-Inversion an
KÄinnen. Da KA und KC keine gemeinsamen Punkte haben und nicht ineinander liegen, also
keine gemeinsamen innere Punkte haben, schneidet die Gerade durch die zugehörigen Raum-Punkte
RA und RC das Paraboloid Par in zwei Punkten zwischen RA und RC und der Raum-Punkt von
KÄinnen liegt unterhalb von Par.

Im ersten Teil der Animation wird P einmal um KA herumgeführt. Die Gerade durch Qa und Qi dreht sich
dabei um einen Punkt der Geraden AC, der die Strecke AC im Verhältnis teilt.
Die Punkte RÄaußen , ParP und ParQa , sowie RÄinnen, ParP und ParQi sind kollinear. Im zweiten Teil
wird der Augenpunkt zur z-Achse hin gedreht. Dann wird bei einem weiteren Umlauf von P um KA durch
die eingezeichneten Zahlen gezeigt, dass das Produkt der Abstände Äaußen von P und Qa , sowie Äinnen
von P und Qi konstant ist, nämlich das Quadrat des Radius von KAaußen bzw. KÄinnen. Im vierten Teil
wird die Potenz-Gerade von KA iund KC hinzugefügt, deren Punkte Zentren eines Potenz-Kreises sind, der
KA iund KC euklidisch orthogonal schneidet. Jeder dieser schwarzen Kreise schneidet auch KÄaußen
orthogonal, nicht aber KÄinnen. Dieser wird in einem Durchmesser von KÄinnen. geschnitten, dessen Mittel-
Senkrechte mit dem Potenzkreis-Zentrum inzidiert.

Nach dem Zurück-Drehen in die Ausgangs-Perspektive wird der Kreis KM1 orangefarben eingezeichnet,
der KA und KC in P bzw. Qa berührt. Die Spur seines Zentrums bei einem Umlauf von P auf KA ist
eine Hyperbel mit den Brennpunkten A und C, da die Differenz seiner Abstände von A und C mit der
Differenz der Radien von KA und KC übereinstimmt. Bemerkenswert ist dabei, dass nicht nur M1 mit
A und P , sowie mit C und Qa kollinear ist, sondern auch RM1 mit RA und ParP, sowie RM1 mit RC
und ParQa. Im letzten Teil der Animation wird das Entsprechende für Kreise um M2 gezeigt, der KA
und KC in P bzw. Qi berührt.

Im Unterschied zur vorherigen Animation schneidet hier die Gerade AC das Paraboloid nicht. Das
bedeutet, dass alle Kreise reell sind, deren zugehörigen Raumpunkte auf AC liegen. Dies gilt auch für
die beiden Kreise um die beiden Ähnlichkeitpunkte Äaußen und Äinnen . Diese schneiden sich hier in
zwei Punkten, die auf allen Kreisen liegen, deren Raum-Punkt auf AC liegt. Sowohl die Inversion an
KÄaußen als auch die an KÄinnen bildet KA in KC ab. Dies macht der Umlauf von P um KA im
ersten Teil der Animation deutlich. Nach dem Wechsel in die Vogel-Perspektive wird dies mit Hilfe der
Abstände wie in der vorherigen Animation gezeigt. Im dritten Teil wird der Kreis um M1 zugefügt, der KA
und KC in P bzw. Qa berührt. Auch hier ist seine Spur eine Hyperbel. Bei einem Stop wird dargestellt,
dass der Kreis um P, Qa und Qi alle anderen Kreise orthogonal schneidet. Im letzten Umlauf von P
wird der Kreis M2 gezeichnet, der KA und KC in P bzw. Qi berührt. Die Spur seines Zentrums ist eine
Ellipse mit den Brennpunkten A und C, da hier die Summe der Abstände von A und C mit der
Summe der Radien von KA und KC übereinstimmt.

Über die Einbettung der Kreis-Geometrie in den dreidimensionalen
projektiv-metrischen Raum

In den vorangehenden Animationen haben wir jedem Kreis in der x-y-Ebene ein Koordinaten-Tripel (x;y;z)
zugeordnet, das einen Punkt P des dreidimensionalen affinen Raums beschreibt. Dabei war (x;y;0) das Tripel
des Kreis-Zentrums und , wenn r der Radius des Kreises ist. Für r = 0 ergibt sich die
Gleichung des nach unten geöffneten Paraboloids Par mit der z-Achse als Symmetrie-Achse
und dem Scheitel-Punkt im Ursprung (0;0;0). Dessen Punkte ordnen wir den 'Null-Kreisen' zu, die wir mit den
Punkten der x-y-Ebene identifizieren. Zu einem Kreis mit positivem Radius r gehört ein Raum-Punkt oberhalb
des Paraboloids. Um auch Punkte darunter zu erfassen, haben wir jeden Kreis mit positivem Radius verdoppelt,
wobei das Duplikat sich nur dadurch vom Original unterscheidet, dass sein Radius und damit
ist und die Farbe seiner Zeichnung aufgehellt. Alle Koordinaten sind also reelle Zahlen.

Spiegelungen im Raum, die zu Kreis-Spiegelungen gehören, kann man in analoger Weise definieren, wie es auf
der Seite ' Spiegelungen 1' dargestellt wird, wobei das Paraboloid dort die Rolle der Kugel-Fläche übernimmt.
Wenn P ein Raum-Punkt ist, der nicht auf Par liegt, und Q ein Punkt auf Par, dann ist das Bild von Q bei
Spiegelung an P der zweite Schnitt-Punkt der Geraden PQ mit Par. Wenn es nur einen Schnittpunkt gibt, also
PQ Tangente ist, fallen Urbild und Bild zusammen. Diese Abbildung für Punkte von Par kann man in gleicher
Weise wie es auf der Seite Spiegelungen 1 beschrieben wird zu einer Abbildung des ganzen Raums
fortsetzen. Dabei hat das Spiegel-Bild von Q das Koordinaten-Tripel des Kreise, der durch Inversion
oder Anti-Inversion des zu Q gehörige Kreises am Kreis zu P gehört.

Analog wie auf der Seite Spiegelungen 1 erweitern wir den affinen Raum zu einem projektiven Raum, um die
metrischen Beziehungen zwischen Kreisen zu erfassen und um Geraden als spezielle Kreise mit unendlich
großem Radius zu deuten. Dazu wird jedes Koordinaten-Tripel p = (x;y;z) zu dem Quadrupel
erweitert, das wir mit allen Quadrupeln identifizieren, die aus durch Multiplikation mit einer reellen Zahl u
ungleich Null entstehen. Zu einem Quadrupel (x;y;z;u) mit u ungleich Null gehört also der affine Punkt mit dem
Tripel (x/u ; y/u ; z/u). Der 'unendlich ferne' Punkt des projektiven Raums auf einer Geraden mit dem Richtungs-
Vektor (x;y;z) wird durch ein Quadrupel ungleich (0;0;0;0) festgelegt.

Eine Gerade in der xy-Ebene wird als Grenzfall eines Kreises mit unendlich großem Radius angesehen. Wenn
die Gleichung dieser Geraden ist, gehört dazu der Raumpunkt mit einem Quadrupel
. Dies gilt zum Beispiel auch für die Tangente an einen Kreis K mit der Gleichung
, dessen Tangente im Punkt die Gleichung

hat.
Ein Quadrupel des zugehörigen Raum-Punkts ist also .

Die Gleichung von Par erweitern wir zu einer Gleichung, die den unendlich fernen Punkt
(0;0;1;0) von Par auf der z-Achse miterfasst, indem wir x, y und z in der Gleichung durch , und
ersetzen und die Gleichung dann mit multiplizieren. Es ergibt sich .

Das Paraboloid Par spielt eine ähnliche Rolle wie die Einheits-Kugelfläche um den Ursprung auf der Seite
Spiegelungen 1. Denn die dort benutzte stereographische Projektion entspricht hier die Projektion parallel
zur z-Achse, da der unendlich ferne Punkt auf der z-Achse auf Par liegt und das Projektions-Zentrum ist.
Die invertierbare projektive Abbildung bildet einen
projektiven Punkt P(x;y;z;u) genau dann in einen Punkt auf der Kugelfläche ab, wenn er auf Par liegt, denn
, wobei der Punkt (0;0;1;0) als Bild den
Südpol -(0:0:-1;1) hat. Der Quadrat-Form der speziellen Relativitäts-
Theorie auf der Seite Spiegelungen 1 entspricht also bei Par die Form , die
wir mit Indizes auch durch darstellen. Die zugehörige symmetrische
Bilinearform ist dann . Sie ist eine nicht-
euklidische Maß-Form , die wir mit f bezeichnen. Die zugehörige Matrix ist 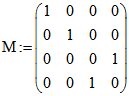, denn
. Punkte P und Q, für die
f(p;q) = 0 ist, werden ' polar' genannt. Die zugehörigen Kreise in der x-y-Ebene sind für polare Punkte
euklidisch orthogonal.

Wegen kann man (wie bei der Kugel) f auch als Maß-Form für Ebenen-Quadrupel benutzen.
Dabei beschreibt das Quadrupel die Ebene E, die genau mit den Punkten P inzidiert,
für die gilt. Wenn Par von E geschnitten wird, ist das Bild der Schnitt-
Kurve bei Projektion parallel zur z-Achse auf die die x-y-Ebene der E zugeordnete Kreis, dem der Pol
von E als Raum-Punkt zugeordnet ist. Dieser Pol ist der gemeinsame Punkt aller Tangential-Ebenen, die
Par in einem Punkt der Schnitt-Kurve berühren. Das Quadrupel des Pols von E ist p = e.M und die zu P
polare Ebene hat das Quadupel e = p.M, da M zu sich selbst invers ist. Dies gilt auch für Ebenen, die Par
nicht schneiden.

Wenn die Ebenen E und D orthogonal sind, dann sind die zugehörigen Kreise in der x-y-Ebene euklidisch
orthogonal.

Die Spiegelung eines Raum-Punkts Q an einem Raum-Punkt P, der nicht auf Par liegt, wird durch
beschrieben oder äquivalent durch .
Dann ist
.
Der Bild-Punkt teilt die Strecke PQ im Verhältnis . Wenn man diese Spiegelungs-
Formel auf einen Punkt Q mit dem Quadrupel in der x-y-Ebene anwendet,
muss man bedenken, dass Q nicht zu einem Null-Kreis gehört, da Q nicht auf Par liegt. Um das Bild
des Punktes Q bei der zu P gehörigen Inversion oder Anti-Inversion zu berechnen, muss man die
Formel auf den unter Q liegenden Punkt ParQ anwenden. Dann erhält man ein Quadrupel, dessen
vierte Komponente nicht 1 ist. Erst nach Division durch diese 4. Komponente ist bei dem Ergrbnis-
Quadrupel (x;y;z;1) das Koordinaten-Paar (x;y) des Bildes vom Nullkreis zu Q bei Inversion oder
Anti-Inversion am Kreis zum Raumpunkt P ablesbar. Für dieses Paar errechnet man den Term
.

Der Anti-Punkt Q* von Q, zu dem der Zwillings-Kreis vom Q gehört, hat für Quadrupel mit vierter
Komponente 1 das Quadrupel . Für das Teilverhältnis von PQ errechnet man dann
.
Wenn P durch den Anti-Punkt P* ersetzt wird, ergibt sich mit Q* das Teilverhältnis
und mit Q das Teilverhältnis einer Anti-Inversion.

Ein Punkt A mit dem Quadrupel heißt 'isotrop' wenn f(a;a) = 0 ist, er also auf
Par liegt, andernfalls heißt er 'anisotrop'. Für alle Punkte über Par ist f(a;a) > 0 , für alle darunter
f(a;a) < 0. Alle anisotropen Punkte A können durch ein 'f-normiertes' Quadrupel (kurz: fn-Quadrupel)
angegeben werden, für das f(a;a) = 1 oder f(a;a) = -1 ist, indem man a durch teilt, denn
. Diese f-Normierung wird benutzt, wenn zu Punkten A
und C ein Punkt B bestimmt werden soll, so dass gilt. Dies ist immer möglich, wenn nach der
f-Normierung f(a;a) = f(c;c) ist. Man wählt dann für b die Summe a + c oder die Differenz a - c.
Man errrechnet dann

.
Dabei können nicht f(a ; a+c) und f(a ; a - c) beide Null sein, denn dann wäre auch f(a ; a) = 0.
Darum hat A das Bild C bei Spiegelung an dem Punkt mit dem Quadrupel a + c oder a - c, wobei
im Allgemeinen beide Möglichkeiten bestehen.

Potenz, Inzidenz und die Maß-Form f

Unter der Potenz eines Punktes P bezüglich eines Kreises K versteht man das Quadrat der Länge
Strecke zwischen P und dem Berühr-Punkt einer der beiden Tangenten durch P an K falls P außerhalb
von K liegt; wenn P innerhalb von K liegt ist die Potenz das Quadrat der halben Länge der Sehne zu K,
die P als Mittelpunkt hat, multipliziert mit -1. Für P auf der Kreis-Linie ist die Potenz gleich Null. Wenn
K mit Zentrum und Radius und in der xy-Ebene liegen, ist die Potenz gleich
. Zu K gehört der Raumpunkt mit ,
wobei für reelle Kreise positiv und für imaginäre Kreise negativ ist. Der zu P gehörige Null-Kreis mit
dem Radius Null hat den Raumpunkt mit auf dem Paraboloid Par. Für
die Potenz errechnet man dann



P inzidiert also genau dann mit K, wenn ist.

Den Begriff Potenz hat man auch für ein Paar zweier Kreise definiert. Wenn wir den Nullkreis durch einen Kreis
mit gleichem Mittelpunkt und dem Radius ersetzen, ist die Potenz mit K durch
festgelegt.