Es lebe die Geometrie!

Penrose-Kachelungen

Die nach Roger Penrose (geboren 1931) benannten aperiodischen Kachelungen verwenden 36°-Rauten und
72°-Rauten mit gleichen Seitenlängen. Dabei wird durch Ausbuchtungen oder Farbmarkierungen erreicht, dass
die Rauten nur in bestimmter Weise aneinander gelegt werden können, so dass es bei keiner Kachelung der
ganzen Ebene eine von der identischen Abbildung id verschiedene Verschiebung gibt, welche die Kachelung
zur Deckung bringt. Keine dieser Kachelungen ist also periodisch. Eine weitere Möglichkeit, die Periodizität
auszuschließen, besteht darin, die Seiten-Strecken durch Seiten-Pfeile zu ersetzen. Diese Möglichkeit
benutzen wir im Folgenden bei den Stern-, Kronen- und Boot-Kacheln der vorangehenden Seite ' Kepler',
um aperiodische Kachelungen vom Penrose-Typ zu konstruieren.

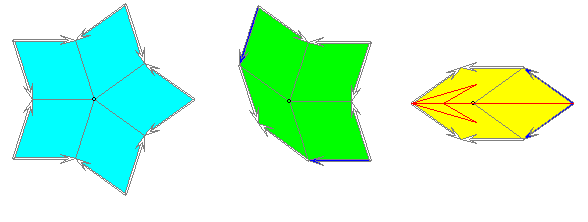
Das Bild zeigt die Zerlegung der Stern-, Kronen- und Boot-Kachel 1. Stufe in 36°- und 72°-Rauten . Der
Kachel-Rand ist ein Pfeilzug statt eines Streckenzugs. Beim Aneinanderlegen der Kacheln müssen die Rand-
Pfeile zur Deckung gebracht werden. Die Rand-Pfeile, deren Spitze keine weitere Rand-Pfeil-Spitze der
gleichen Kachel trifft, wurden blau statt grau gezeichnet. Als Anlege-Bedingung würde reichen, zu verlangen,
dass diese Pfeile zur Deckung gebracht werden müssen. Denn dann ist die Bedingung für die grauen Pfeile
auf Grund der Form erfüllt. Der Punkt im Innern der Kacheln, an dem die Rauten zusammentreffen, sei
'Zentrum' der Kachel genannt. Bei der Boot-Kachel ist ein roter Pfeil zur Markierung einer Orientierung
gezeichnet, dessen Richtung mit der Richtung der Resultierenden der grauen Randpfeile übereinstimmt.
Diese Kacheln wurden gelegendlich als Henley-Kacheln bezeichnet (nach C. Henley, Phys.Rev. 34 (1986)).

Wir nennen eine Kachel 'innere Kachel', wenn auf allen ihren Seiten Kacheln nach dieser Regel anschließen.
Dann gilt folgender Satz (siehe Edzard Salow, Über eine Penrose-Kachelung, Der mathematisch-
naturwissenschaftliche Unterricht 2006, Heft 2):

Wenn alle an eine innere Stern-Kachel angesetzten Kacheln ebenfalls innere Kacheln sind, dann gehört
sie zu einem Kachel-Komplex, der kongruent ist zu einem der in der folgenden Abbildung dargestellten
Komplexen.

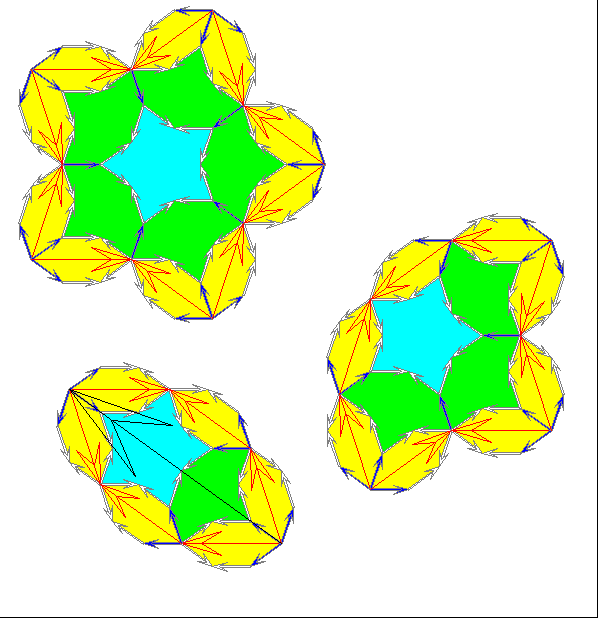
Wir nennen diese Kachel-Komplexe Stern-, Kronen- bzw. Boot-Kachel 2.Stufe. Die roten Pfeile auf
der Symmetrie-Achse der Boot-Kacheln 1. Stufe bilden Pfeilzüge, die kongruent sind zu den Rand-
Pfeilzügen der Kacheln 1. Stufe. Darum führt die Anlege-Regel für Kacheln 1. Stufe zu einer analogen
Regel für Kacheln 2. Stufe, so dass sich Kacheln 3. Stufe ergeben, und so weiter. Beim Anlegen der
Kachel n. Stufe überlappen sie sich in den Boot-Kacheln (n-1). Stufe. Jede Kachel beliebiger Stufe
lässt sich zu einer lückenlosen Kachelung der ganzen Ebene vervollständigen. Jede dieser Kachelungen
enthält Boot-Kacheln, Kronen-Kacheln und Stern-Kachel jeder Stufe, und keine ist periodich.

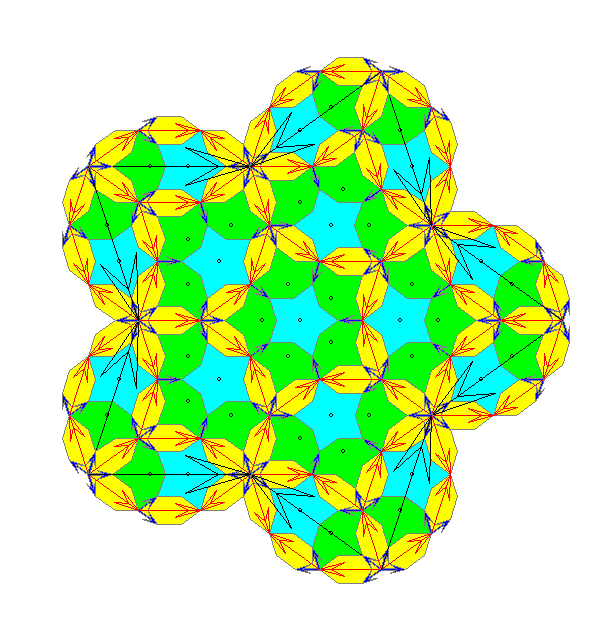
Hier sieht man Stern-, Kronen- und Boot-Kacheln 3. und 4. Stufe.

Die Gleitschau zeigt die Boot-Ränder von Kacheln 2., 3. und 4. Stufe, die sich aus einer Kachel
gleicher Art in Stufe 1 ergeben. Die Seitenlängen der äußersten hellgrünen Boot-Kacheln 1. Stufe
stimmen mit den Seitenlängen der roten Kachel im Zentrum überein. Die Länge des Pfeils auf der
Symmetrie-Achse jeder Boot-Kachel ergibt sich aus der Länge seiner Seiten durch Multiplikation
mit den Quadrat der großen goldenen Zahl . Das Zentrum teilt diesen Pfeil im
goldenen Schnitt.

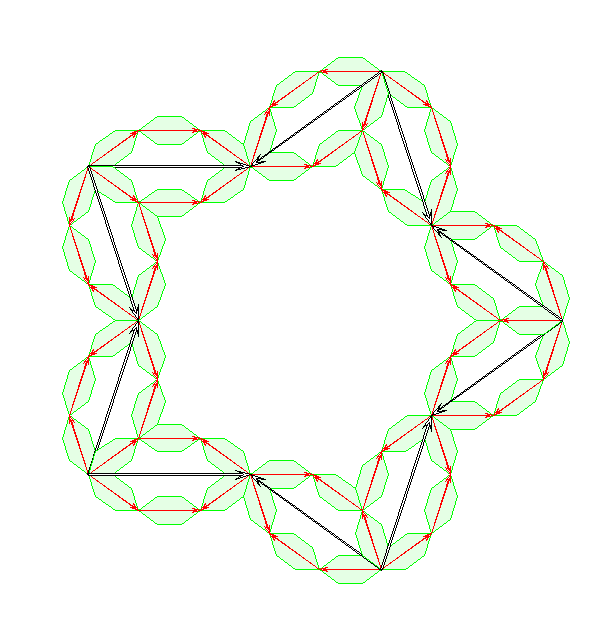
Hier wurden die Randpfeile der Kacheln 1. Stufe um die Boot-Kacheln ergänzt, zu denen sie die
Mitten Pfeile sind; und dieser Prozess wurde anschließend bis zur 6. Stufe auf die neuen Boot-Kacheln
fortgesetzt. Auf diese Weise ergeben sich am Rand immer kleinere Boot-Kacheln, deren Seitenlänge
jeweils mit dem Faktor gegenüber der vorhergehenden Stufe abnimmt. Zum Teil wurden nur die
äußeren Hälften des Randes der Boot-Kacheln gezeichnet.

Wenn man die Schildkröte den Rand der Boot-Kachel n-ter Stufe gegen den Uhrzeigersinn durchlaufen
lässt, dann muss sie an jeder Ecke die Richtungsänderung kennen. Von den beiden Ecken,
die auf der Haupt-Symmetrieachse liegen, habe die im größeren Abstand vom Zentrum die Nummer 0.
Für n = 0 verlaufe der Weg zwischen diesen beiden Punkten geradlinig hin und zurück. Dann wird die
Änderung der Zahl k im Eckpunkt mit der Nummer durch die Funktion dk beschrieben.
Dabei sind die Verknüpfungen div und mod für ganze Zahlen i und m durch folgende Gleichung bestimmt:
. Dabei ist .

function Tform1.dk(n,i:integer):integer;
begin
if n=0 then result:=5
else if i mod 3=0 then result:=(dk(n-1,i div 3)+8) mod 10
else result:=1;
end;

Die Schildkröte durchläuft auf ihrem Weg um die Boot-Kachel den i-ten Randpfeil in Gegen-Richtung genau
dann, wenn die folgende Funktion f den Wert 1 hat:

function f(n,i:integer):integer;
begin
if n=0 then result:=i
else if i mod 3 = 1 then result:=f(n-1,i div 3)
else result:=(i mod 3) div 2;
end;

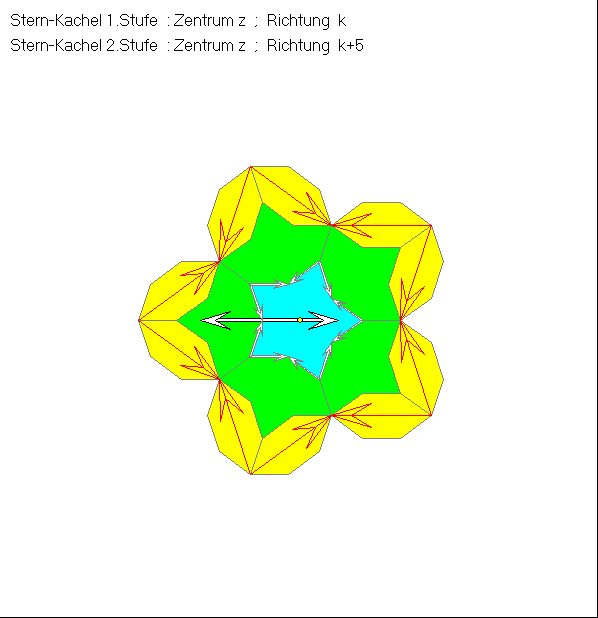
Die Gleitschau zeigt die Möglichkeiten, eine Kachel der Stufe n (mit grauen und blauen Rand-Pfeilen)
zu einer Kachel der Stufe n+1 (ohne Rand-Pfeile) zu erweitern am Beispiel der Stufen n = 1 und n = 2.
Die Orientierung der Kacheln wird hierbei mit Hilfe eines weiß gefüllten Pfeils fixiert, der an das Zentrum
der Kachel angeheftet ist. Er liegt bei allen drei Kachel-Typen auf einer Symmetrtieachse und ist auf eine
Spitze mit dem Innenwinkel 72° gerichtet. Bei den Boot-Kacheln stimmt dies mit der oben definierten
Orientierung überein, die bei den Boot-Kacheln 1. bzw. 2. Stufe durch die roten bzw. schwarzen Pfeile
markiert ist. Die Länge der Zentrumspfeile ist bei den Kacheln 1. Stufe gleich der Seitenlänge und bei den
Stufen n > 1 gleich der Länge der zugehörigen Boot-Kacheln der Stufe n - 1. Die Länge des Zentrums-
Pfeils zur Stufe n+1 ergibt sich aus der in der Stufe n durch Multiplikation mit dem Quadrat der goldenen
Zahl G. Der zum Zentrums-Pfeil der Ausgangs-Kachel gehörige Vektor wird hier mit bezeichnet,
wobei die ganzzahlige Richtungszahl k zwischen 0 und 9 zu dem Richtungswinkel gehört.

Es gibt 11 Möglichkeiten, eine Stern-Kachel zu einer Kachel der nächsten Stufe zu erweitern,
5 Mölichkeiten für eine Kronen-Kachel und 16 für eine Boot-Kachel. 5 Möglichkeiten führen
zum Beispiel eine Stern-Kachel (Abkürzung S) in Kronen-Kacheln (Abkürzung K) der nächsten
Stufe über. Wir bezeichnen diesen Übergang durch die Funktion mit , und
entsprechend für die anderen Übergange. Jede Kachelung der ganzen Ebene kann dann durch
Angabe einer Ausgangs-Kachel und einer unendlichen Folge von derartigen Funktionen beschrieben
werden. Bei einer gegebenen Kachelung ist dann nach der Wahl einer beliebigen Ausgangs-Kachel
(beliebiger Stufe) die Folge der Funktionen durch die Kachelung eindeutig festgelegt.

Es ist eine offene Frage, welche der so gebildeten Kachelungen der ganzen Ebene kongruent sind,
also durch eine Bewegung ineinander übergehen.

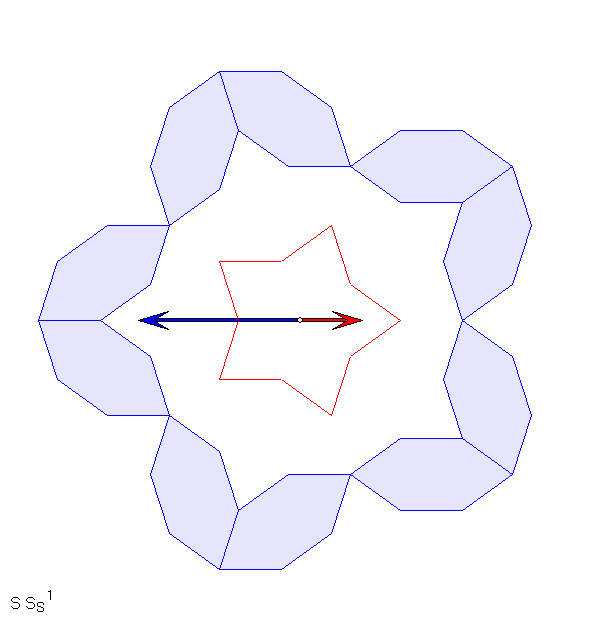
Die Gleitschau zeigt Anfänge von Erweiterungsfolgen nach dem oben angegebenen Prinzip.