Es lebe die Geometrie!

Kopunktale Astroiden-Tangenten

Durch jeden Punkt P im Innern einer Astroide, der nicht auf den Symmetrieachsen durch die Spitzen
liegt, gibt es vier Tangenten. Wenn die Astroide durch die Funktion
gegeben ist, gibt den Richtungswinkel der Tangente im Punkt an. Der Punkt mit
den kartesischen Koordinaten liegt auf der Tangente und auf dem Kreis
um den Ursprung, der die Astroide berührt. Wir nennen diesen Punkt 'Basispunkt der Tangente' und
den zugehörigen Ortsvektor 'Basispfeil'. Die folgende Slideshow zeigt den Zusammenhang zwischen P
und den Basispfeilen der vier Tangenten durch P.

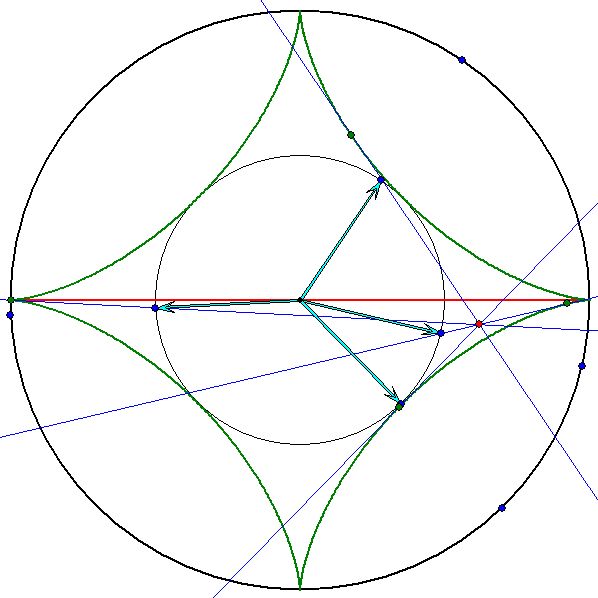
Bild 1 zeigt die vier Tangenten durch den roten Punkt P mit den hellblau gezeichneten Basispfeilen.

Bild 2 zeigt, dass die Vektorsumme dieser Basispfeile der Ortsvektor von P ist.

Bild 3 zeigt, dass die Vektorsumme zweier Basispfeile orthogonal zu dem Vektor ist, der durch
Spiegelung der Summe des dritten uind vierten Basispfeils an der Rechtsachse entsteht. Daraus
folgt, dass die Summe der Richtungswinkel aller vier Basisvektoren gleich 180° beträgt.

In Bild 4 wurden die sechs magenta-farbenen Mittelpunkte zu den vier blauen Punkte Q1, Q2, Q3, Q4
auf dem Rastkreis eingezeichnet, die mit jeweils einem Basispunkt und dem Ursprung kollinear sind.

Bild 5 zeigt, dass P der Euler-Poncelet-Punkt der vier Punkte Q1, Q2, Q3, Q4 ist. Dies bedeutet,
dass die Neun-Punkte-Kreise der Dreiecke Q1 Q2 Q3, Q1 Q2 Q4, Q1 Q3 Q4 und Q2 Q3 Q4 sich
in P schneiden. Zur Definition des Euler-Poncelet-Punktes siehe die Encyclopedia of Quadri-Figures .

Zur Begründung von Bild 2:

ist die hessesche Nornalform der Tangenten-Gleichung zum
Richtungswinkel mit dem Basispunkt . Setzt man an die
Stelle von und ersetzt dann durch c, so ergibt sich nach geeignetem Quadrieren die
Gleichnung . Nach dem Satz von Vieta für ganzrationale
Gleichungen vierten Grades ist die Summe der vier Lösungen für c bei konstantem x und y der Koeffizient
von mit entgegengesetztem Vorzeichen, also . Für die vier Richtungswinkel der Basispfeile gilt
darum . Ersetzt man nicht , sondern , dann
ergibt sich analog . Darum ist P(x ; y) der Punkt
, sein Ortsvektor also die Vektorsumme der vier Basispfeile.

Zur Begründung von Bild 3:

Man errechnet . Dies ist also
eine komplexe Zahl mit dem Argument (Richtungswinkel) . Das gilt darum auch für die Zahl
, so dass
einen Punkt auf der Tangente
mit dem Richtungswinkel angibt. Analog zeigt man, dass der gleiche Punkt auch auf der Tangente
mit dem Richtungswinkel liegt. Darum muss er mit P übereinstimmen. Also ist wegen der Aussage
von Bild 2 . Da der Pfeil vom Basispunkt
zum Basispunkt orthogonal zu dem vom Ursprung zum Punkt
ist, folgt daraus die Aussage von Bild 3.