Es lebe die Geometrie!

Hintereinanderschaltungen von Spiegelungen
elliptisch, euklidisch, hyperbolisch

--> Die Psdeudosphäre und die hyperbolische Geometrie
https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Der schwarz gezeichnete Umriss der Ziege wird hier an den Kugelflächen-Kreisen a, b und c
gespiegelt. Oben links bzw. rechts wird das zugehörige Bild im Klein- bzw. Poincare-Modell
gezeigt, das durch Zentralprojektion auf die Tangentialebene im Nordpol mit dem Zentrum im
gelb umrandeten Punkt Z bzw. im Südpol entsteht. Für Z innerhalb bzw. auf bzw. außerhalb
der Kugelfläche sind die Spiegelungen an den Geraden im Klein-Modell elliptisch bzw. euklidisch
bzw. hyperbolisch. Im Poincare-Modell ergeben sich in jedem Fall Spiegelungen.an euklidischen
Kreisen. Die Wirkung einer Hintereinanderschaltung zweier Spiegelungen zeigt sich an dem
Zusammenhang zwischen der roten, grünen und blauen Ziege. Diese Bilder gehen durch eine
Drehung um Dreiecks-Eckpunkte auseinander hervor.

Der zeitweise sichtbare schwarze Kugelflächen-Kreis hat Z als Pol. Er ist orthogonal zu a, b und c.
Sein Bild im Klein-Modell gibt im hyperbolischen Fall die äußere Begrenzung der Punktmenge des
Modells an.

Die Spiegelbilder der Ziege erscheinen im Klein- und im Poincare-Modell nur dann unverzerrt, wenn
Z im Südpol liegt. Die Abstands-Bestimmung zweier Punkte ist aber auch im elliptischen und im
hyperbolischen Fall so definiert, dass die elliptischen bzw. hyperbolischen Abstände im Bild der
Ziege mit dem im Spiegelbild übereinstimmen.

Die Animation stellt Drehungen um den Punkt A als Hintereinanderschaltung der Spiegelungen
an dem festen Kugelflächen-Kreis g und dem bewegten Kreis h dar. Die Ebenen dieser beiden
Kreise gehen durch den gelb umrandeten Punkt Z, der verschiedene Orte der z-Achse durchläuft.
Die zwischen g und h angezeigte Winkelgröße gilt auch für das Klein-Modell und das Poincare-
Modell, unterscheidet sich aber beim Klein-Modell von der euklidischen Winkelgröße, es sei denn,
dass Z mit dem Südpol zusammenfällt. Die Winkel sind hier 'modulo 180° ' angegeben; das heißt,
dass z. B. die Winkelgröße -60° mit der Größe 120° identifiziert wird. Die Größe des Winkels
zwischen g und h stimmt (euklidisch) mit der zwischen den Geraden durch A und den Polen von
g und h überein. Der Pol von h bewegt sich bei der Drehung auf der zur Geraden AZ polaren
Geraden. Diese Gerade liegt in der zum Punkt Z polaren Ebene durch den zeitweise sichtbaren
schwarzen Kugelflächen-Kreis, der zu g und h orthogonal ist. Dieser schwarze Kreis bestimmt im
hyperbolischen Fall den Rand des Klein-Modells.

Für Z im Kugelmittelpunkt ist die Hintereinanderschaltung von Spiegelungen an g und h eine eulidische
Drehung des Raumes. Auf der Kugeloberfläche erscheint die blaue Ziege gegenüber der schwarzem um
einen Winkel gedreht, der euklidisch doppelt so groß ist wie der Winkel zwischen g und h. Im Klein- oder
Poincare-Modell sind die Ziegen dann aber gegeneinander verzerrt, da es sich hier um keine euklidische
Drehung handelt, man also von einer Verdopplung nur im Sinne einer nicht-euklidischen Winkelmessung
reden kann. Für Z im Südpol ergibt sich im Klein- oder Poincare-Modell zwar eine euklidische Drehung
mit euklidischer Verdopplung des Winkels zwischen g und h. Dann handelt es sich auf der Kugel aber um
keine euklidische Drehung.

Die beiden dunkelblauen Kugelflächen-Kreise g und h sind hier orthogonal zu dem hellblauen Kreis j.
Die Ebenen, in denen g, h und j liegen, enthalten auch Z. Die Hintereinanderschaltung der Spiegelungen
an g und h ergibt dann im euklidischen Fall eine Translation. Im Klein-Modell oben links wird dies an der
Verschiebung der Ziege parallel zum Projektionsbild j' von j deutlich, falls der gelb umrandete Punkt Z im
Südpol der Kugel liegt.

Im hyperbolischen Fall, also wenn Z außerhalb der Kugel liegt, wird die Ziege im Klein-Modell so
bewegt, dass der hyperbolische Abstand von j' unverändert bleibt. Auch die hyperbolischen Abstände
zwischen entsprechenden Punkten im Bild der Ziege bleiben bei der Hintereinanderschaltung der
Spiegelungen an g und h unverändert, obwohl die euklidische Bildgröße bei Annäherung an den schwarzen
Kreis immer kleiner wird.

Entsprechendes gilt im elliptischen Fall, wenn also Z im Innern der Kugel liegt. Die Hintereinanderschaltung
der Spiegelungen an g und h ist dann eine Drehung um die Schnittpunkte der Geraden durch Z und den Pol
von j mit der Kugelfläche. Falls g orthogonal zu h ist, hat sie im Klein-Modell die gleiche Wirkung wie die
Spieglung an j'. Darum erscheint das verschobene Bild der Ziege auf beiden Seiten von j'.

Zur Berechnung von Hintereinanderschaltungen von Spiegelungen

Auf der Seite Spiegelungen 1 wird gezeigt, dass die Spiegelung zu einem Punkt P des projektiven
Raums mit Hilfe eines Koordinaten-Quadrupels durch
beschreiben lässt. Dies ist eine lineare Abbildung des Vektorraums aller Quadrupel aus reellen
Zahlen. Für die symmetrische Bilinearform gilt dabei
. Die Quadrupel , für die gleich Null ist, gehören zu den projektiven
Punkten der Polarebene von P. Sie bilden in einen dreidimensionalen Unter-Vektorraum, für dessen
Elemente gilt, so dass die zugehörigen projektiven Punkte also festbleiben. Zusammen mit
charakterisiert diese Eigenschaft vollständig. Das heißt, dass eine lineare Abbildung
des mit diesen beiden Eigenschaften notwendig sein muss.

Wir nennen Punkte X mit 'polar' zu P.

Für die Hintereinanderschaltung der Spiegelungen an den projektiven Punkten P und Q gilt:

Wenn das Quadrupel in dem von und aufgespannte Vektorraum liegt, wird es in ein Quadrupel
des gleichen Vektorraums abgebildet. Die projektiven Geraden PQ durch P und Q bleibt also als Ganzes
fest, wenn auch nicht punktweise. Die dazu polare Gerade ist die Schnittmenge der Polarebenen von
P und Q. Für alle Quadrupel des zugehörigen zweidimensionalen Vektorraum gilt .
Die Punkte von h bleiben also bei punktweise fest.

Es sei X ein Raumpunkt auf der Geraden durch die Punkte P und Q außerhalb der Kugeloberfläche.
Dann gibt es reelle Zahlen u, v mit . Aus der quadratischen Gleichung

folgt, dass die Gerade PQ die Kugeloberfläche in zwei einem bzw, keinem Punkt schneidet, je
nachdem die Diskriminante größer, gleich bzw. kleiner als Null ist.
Für einen Schnittpunkt X mit der Oberfläche gilt dann . Aus
folgt dann, dass X nur dann polar zu P ist,
wenn PQ die Kugeloberfläche in genau einem Punkt trifft.

Der obige Term für zeigt, dass genau für gilt. Wenn eine
Gerade durch P und Q die Kugeloberfläche nicht in genau einem Punkt trifft, dann gibt es auf PQ
genau einen Punkt R, der polar zu P ist, nämlich der Punkt zum Quadrupel , und
für diesen gilt , so dass also die Spiegelung an R existiert.

Wenn die Gerade PQ die Kugel nicht schneidet, trifft die dazu polare Gerade die Kugeloberfläche in zwei
Punkten A und B, deren Tangentialebenen sich in PQ schneiden. ist dann eine im Allgemeinen
nicht-euklidische Drehung um AB. Als Größe des Drehwinkels kann man das Doppelte der euklidische
Winkelgröße zwischen den Kugelkreisen zu P und Q ansehen. In der Tangentialebene von A
verläuft die Strecke AP bzw. AQ senkrecht zu dem zu P bzw. Q gehörigen Kreis. Darum stimmt
mit der euklidischen Größe des Winkel PAQ überein. Definiert man , so gilt
dabei . Man erkennt dies, wenn man alle Raumpunkte so um das Kugekzentrum N
dreht, dass B in den Südpol fällt. Die Bilder der Kugelkreise von P und Q bei der stereographischen
Projektion sind dann Geraden, die sich im Bildpunkt von A euklidisch unter der Winkelgröße schneiden
und deren Lotgeraden auf den Bildern von P bzw. Q liegen. Diese Bilder von P und Q sind unendlich ferne
Punkte in der Tangentialebene des Nordpols.

P und Q seien nun Punkte außerhalb der Kugel, für welche die Gerade PQ die Kugeloberfläche in zwei
verschiedenen Punkten A und B schneidet. Die dazu polare Gerade, also der Schnitt der Polarebenen
von P und Q, trifft die Kugeloberfläche dann nicht. Die zu P und Q gehörigen Kreise haben dann keinen
gemeinsamen Punkt. Die Größe hat auch hier eine geometrische Bedeutung, allerdings nicht für
einen Winkel, sondern für das Doppelverhältnis 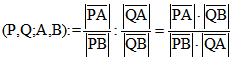der vier Längen
, , und . Es gilt nämlich . Dieser Zusammenhang
ist der Gleiche wie in der zweidimensionalen hyperbolischen Geometrie. Definiert man wie dort einen
hyperbolischen Abstand , so folgt .
(siehe z. B. http://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf S.80).

Satz: P, Q und S seien kollineare Punkte des projektiven Raums, die nicht auf der Oberfläche der
Einheitskugel liegen und deren Verbindungsgerade nicht genau einen Punkt mit der Oberfläche
gemeinsam hat. Dann gilt:

1. Sei . Dann liegt der zugehörige Punkt R ebenfalls auf
PQ, aber nicht auf der Fläche der Kugel, und es ist , also .
2. Wenn , dann stimmen die Geraden PQ und RS überein und zu R gehört das
Quadrupel .

Beweis : Im Fall P = Q oder Q = S sind die Behauptungen offenbar erfüllt, auch im Fall P = S,
denn dann ist . Darum sei im Folgenden vorausgesetzt, dass P, Q und S paarweise
verschieden sind-
Zur 1. Behauptung : Sei , und
. Dann ist
und analog . Wenn die Quadrupel mit dem Strich nicht das Null-
Quadrupel sind, gehören sie darum zu den Punkten P', Q' und S', die auf der Geraden
PQ polar zu P, Q bzw. S sind. Darum ist
.
Zwei Vorzeichen sind im letzten Term also geändert. Analoge Überlegungen zeigen dann
.

Sei , ,
und . Wie oben folgt
. Darum gehören die Quadrupel mit zwei Strichen
zu P, Q bzw. S, da diese Punkte die einzigen zu P', Q' bzw. S' polaren Punkte auf PQ
sind. Also ist
Durch Wiederholung dieses Arguments ergibt sich .

Die Determinante det der Matrix 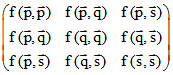ist Null, da , und linear
abhängig sind. Damit errechnet man
, so dass R nicht auf der
Fläche der Kugel liegen kann. Entsprechendes gilt für R'.

Die Gleichung
und Entsprechende für
und zeigen, dass , also R' polar zu R ist. bildet
darum die Quadrupel der Punkte von PQ wie ab. Für jeden Punkt X auf der zu PQ
polaren Gerade gilt dies auch, denn . Darum
ist .


Wegen ist
, so dass der Winkel bzw. der
Abstand zu den Paaren (P,Q) und (R,S) übereinstimmt.