Es lebe die Geometrie!

Konjugierte Polaren einer Kubik aus der Prabel und der Geraden y = 0,2x - 1

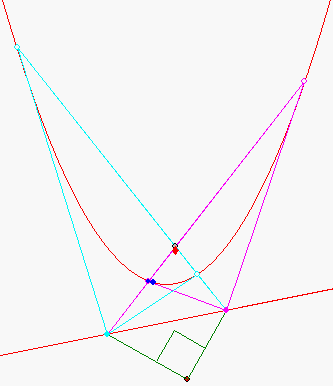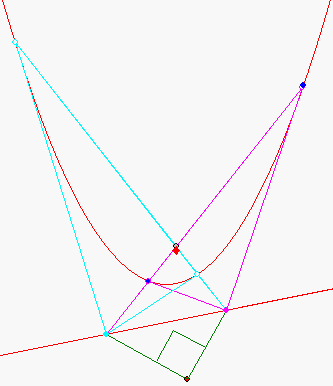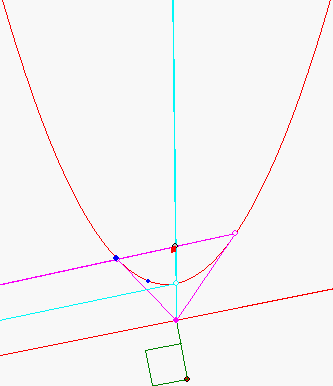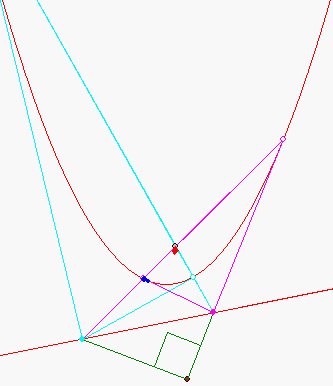
Die beiden Polaren der Punkte A (magenta) und B (hellblau) auf der Geraden g : y = 0,2x - 1 schneiden sich im Allgemeinen nicht senkrecht, der Schnittpunkt P ist aber stets der Gleiche. P wird 'Pol' von g genannt.
Der Winkel AMB am Maßpunkt M(0,6923 ; -2,7284) zwischen den grün gezeichneten Strecken beträgt stets 90°. M lässt sich bei gegebener Parabel und Gerade dadurch bestimmen, dass man zwei Thaleskreise über AB in verschiedenen Pasitionen dieser beiden Punkte schneidet. Die Verbindungsgerade von P mit dem Berührpunkt der Tangente an die Parabel, die parallel zu g ist, schneidet dann g in dem Lotfußpunkt des Lots vom Maßpunkt M auf g .