Es lebe die Geometrie!

Das Beltrami-Klein-Modell

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Das Beltrami-Klein-Modell (kurz: Klein-Modell) wurde von Felix Klein (1848-1925) im Jahr 1871
angegeben. Ideen dazu sind in Arbeiten von Eugenio Beltrami (1835-1900) aus dem Jahr 1868 angelegt.
Die Punkte des Beltrami-Klein-Modells (K-Punkte) sind die Punkte einer Ebene im Innern eines Kreises
mit dem Radius 1. Die K-Geraden sind die Sehnen dieses Einheitskreises, wobei die Enden auf dem
Kreis nicht dazu gehören. Wenn g eine K-Gerade mit dem Mittelpunkt M und den Enden E und F ist
und P eine K-Punkt auf g, dann ist sein nicht-euklidische Abstand (K-Abstand) von M der Betrag von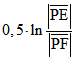
. Dabei ist der euklidische Abstand von P und E. Andere Abstände ergeben sich
daraus durch Differenzbildung. Zur Bestimmung von K-Winkelgrößen ordnet man jeder K-Geraden g
den Kreisbogen durch seine Enden zu, der senkrecht auf dem Einheitkreis steht. Der Mittelpunkt des
zu diesem Bogen gehörigen Kreises ist der Pol P der Geraden, von der die K-Gerade g ein Teilstück
ist. P ist der Schnittpunkt der Einheitskreis-Tangenten in den Enden von g. Die K-Größe des Winkels
zwischen zwei K-Geraden ist die euklidische Größe des Winkels zwischen den zugeordneten Kreisbögen.

Wenn (p;q) die kartesischen Koordinatendes Punktes P der Ebene ist, dann ist er Pol der Geraden mit
der Gleichung . Dies ist die 'Polare' von P. Um auch einer K-Geraden g durch den
Einheitskreis-Mittelpunkt einen Pol eindeutig zuzuordnen, definiert man einen 'unendlich fernen Punkt',
der auf allen Geraden liegt, die euklidisch orthogonal zu g sind. Der zugeordnete Kreisbogen ist g selbst.

Für die Berechnung von K-Maßen ist der Term 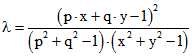von zentraler Bedeutung.
P und X seien die Punkte der Ebene mit den kartesischen Koordinaten-Paaren (p; q) und (x;y).
Wenn P und X K-Punkte sind, dann ist ihr K-Abstand und .
Wenn P und X Pole von schneidenden K-Geraden sind, dann gilt für die K-Winkelgröße .
Die Geraden sind insbesondere genau dann K-orthogonal wenn ist.
Haben die Geraden ein gemeinsames K-Lot, dann ist ihr Abstand und .
In dem Fall ist das K-Lot eindeutig bestimmt und der Abstand der Geraden ist der Abstand der Lotfußpunkte.
Wenn P Pol einer K-Geraden g ist und X ein K-Punkt, dann ist der K-Abstand von g
und . Der K-Abstand von P und g stimmt mit dem von P zum Fußpunkt des K-Lots von P
auf g überein.

Die grünen Ellipsen sind in dieser Animation K-Kreise mit dem grauen Punkt P(p;q) als K-Zentrum
und K-Radien, die Vielfache von 0,2 sind. Ihre Gleichung hat die Form
mit , wobei
den Radius angibt. Der magenta-rote K-Kreis gehört zu und . Die Pole der
Tangenten an diesen K-Kreis liegen aud der blauen Ellipse außerhalb des Einheitskreises, deren
Gleichung ebenfalls die obige Form hat. Ihr Lambda-Wert ist .

Hier wird die schwarze K-Gerade g mit dem grauen Pol P von der magenta-roten K-Geraden h in
dem hellblauen K-Punkt Q geschnitten. Die zugeordneten Kreisbögen schneiden sich in dem K-Punkt
Q', der ebenfalls hellblau ist. Q' ist der K-Mittelpunkt von Q und dem Zentrum Z des schwarzen Kreises.
Das bedeutet, dass der K-Abstand von Q' zu Q mit dem von Q' zu Z übereinstimmt. Die K-Größe des
Schnittwinkels von g und h ist die euklidische Größe des Winkels zwischen den zugeordneten Kreisbögen.
Sie beträgt in jeder Position von h 45°. Der rote Pol R von h bewegt sich auf der roten Hyperbel mit
der Gleichung .
Die blaue Gerade j schneidet g ebenfalls unter der K-Winkelgröße 45°, allerdings mit anderer
Orientierung. Der blaue Pol S von j liegt hier anders als in der folgenden Animation auch auf der gleichen
Hyperbel. j ist Tangente an die Hyperbel im Pol R von h. h ist Tangente an die Hyperbel im Pol S
von j. P, R und S liegen auf der schwarz gezeichneten Geraden k, die g im grauen Punkt T schneidet.
Die Gerade Q'S ist Tangente an der Kreisbogen zu h und Q'T ist Tangente an den Kreisbogen zu g.

Anders als in der vorangehenden Animation ist hier die Hyperbel in eine magenta-rote und eine blaue
aufgespalten. Beide haben eine Gleichung in der Form

mit dem Lambda-Wert 0,45 bei der roten und 0,55 bei der blauen Hyperbel. Die K-Größen der
Schnittwinkel von der roten Geraden h bzw. der blauen Geraden j mit der schwarzen Geraden g
betragen ungefähr 47,9° bzw. 42,1°.

Jede der grünen Ellipsen ist der geometrische Ort der Punkte, die von der schwarzen K-Geraden g
einen konstanten Abstand haben. Die Abstände sind Vielfache von 0,2. Diese K-Abstandskurven
haben ebenfalls die Gleichung , wobei (p;q) die
kartesischen Koordinaten des Pols von g sind, hier (1,5 ; 1,5). Der Lambda-Wert der Abstandsurven
ist stets negativ. Für die magentafarbene Abstandskurve beträgt er -2, der Abstand dazu ist ungefähr
1,15. Die Pole der Tangenten an diese Abstandskurve liegen auf der blauen Ellipse, die ebenfalls eine
Gleichung in der obigen Form hat, hier ist .