Es lebe die Geometrie!

Steiner-Zykloide und Drehpunktfunktion

Die Steiner-Zykloide kann mit Hilfe von komplexen Zahlen als Graph der Funktion
beschrieben werden. In kartesischen Koordinaten werden die Punkte der Zykloide also durch Paare
mit Winkelgrößen zwischen 0° und 360°
beschrieben. Eine alternative Möglichkeit zur Untersuchung bietet die Drehpunktfunktion. Dabei stellt man
sich eine Zahlengerade g vor, die in der Ebene bewegt wird. h sei die Parallelen zu einer festen Rechtsachse
in der Ebene durch den Punkt mit der Koordinate Null des eindimensionalen Koordinatensystems auf g. Die
Größe des Winkels zwischen h und der Strecke von diesem Nullpunkt zum Punkt auf mit der '1' sei mit
bezeichnet und 'Richtungswinkel von g' genannt. Die Bewegung von g kommt ausschließlich durch eine
Drehung gegen den Uhrzeigersinn um einen von abhängigen Drehpunkt auf g zustande. Die Lage
des Drehpunkts wird durch eine Funktion festgelegt, wobei die Zahl ist, die in dem
eindimensionalen Koordinatensystem von g an der Stelle von steht. Im Koordinatensystem der Ebene
wird dann die Drehpunktkurve durch die Funktion 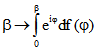dargestellt, falls dieses Stieltje-Integral
existiert, oder für ein stetig differenzierbares f durch das Riemann-Integral 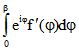. (Siehe die Pdf-Datei

http://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf. ) Dabei wird davon ausgegangen, dass g für
mit der Rechtsachse des Koordinatensystems der Ebene zusammenfällt. Die Evolvente der
Drehpunktkurve durch den Punkt (s ; 0) wird durch 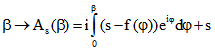beschrieben.

Bei der Steiner-Zykloide benutzen wir die Drehpunktfunktion . Für
wachsendes durchläuft dann eine Steiner-Zykloide im Uhrzeigersinn. Der Rastkreis dieser
Zykloide hat den Radius 9/8.

In den folgenden Animationen werden diese Zusammenhänge dargestellt. Außerdem wird die Umfangslänge
von Tangenten-Vielecken verschiedener Evolventen untersucht.

In dieser Animation werden für die roten Evolventen der blauen Steiner-Zykloide zu s gleich 1,
0,6 und 0,2 die Tangenten-Vierecke dargestellt, bei denen aufeinanderfolgende Tangenten einen
rechten Winkel bilden. Die jeweils aktuelle Lage des Tangenten-Vierecks wird durch den langen
Pfeil bestimmt, der die Steiner-Zykloide in dem gelben Punkt berührt. Dieser Pfeil liegt auf g mit
der Spitze bei '1', dem Ende bei '-1' und der Mitte bei '0'. Die grüne oder rote Markierung gibt den
Funktionswert von f an, der gleichartig auch im Graph darüber angezeigt wird. Der blaue Tangenten-
Pfeil steht senkrecht auf diesem g-Pfeil, so dass seine Spitze relativ dazu nach links gerichtet ist.
Die unten angezeigten Seitenlängen beziehen sich auf die Längen dieser Tangenten-Pfeile. Die Werte
sind konstant 2s. Bei der Evolvente zu s = 0,2 ist bemerkenswert, dass die Berührpunkte außerhalb
der Tangentenpfeile liegen.

Für das Steiner-Gleichdick, also die Spitzen-Evolvente der Steiner-Zykloide werden die Tangenten-n-Ecke
mit gleichen Innenwinkeln für n gleich 5, 6, 7 und 8 gezeigt. Ihre Umfangslänge ist konstant .

Diese Animation zeigt die Tangenten-Pfeilecke der Bogenmitten-Evolvente zur Steiner-Zykloide
für die Eckenzahlen n gleich 3, 5 und 7. Der Richtungswinkel der Zahlengeraden g bestimmt die
blaue Tangente. die orthogonal zur Geraden g durch ihren Nullpunkt verläuft. Wenn um
vergrößert wird, ergibt sich analog die dunkelgrüne Tangente usw., so dass sich aufeinander folgende
Tangenten unter einem Winkel von schneiden. Auf den Seiten des Tangenten-n-Ecks wird
durch einen Pfeil eine Orientierung so bestimmt, dass bei einem Durchlauf die Differenz aufeinander
folgender Richtungswinkel beträgt. Wenn bei diesem Umlauf eine Seite gegen die Richtung
ihres Pfeiles durchlaufen wird, muss die zugehörige Seitenlängen mit einem Minus-Zeichen versehen
werden. Bei den Eckenzahlen 5 und 7 ergibt sich dann bemerkenswerter Weise bei der Evolvente
der Steiner-Zykloide zu s = 0 stets die Umfangslänge Null.