Es lebe die Geometrie!

Dorn und Blatt und Streckspiegelung

Unter einer 'Streckspiegelung' (oder 'Klappstreckung') verstehen wir die Hintereinanderschaltung
von einer Achsen-Spiegelung und einer Streckung im . Wenn man die Punkte (x ; y) als Spalten
mit dritter Komponente 1 darstellt ('projektive Darstellung'), dann gibt es zu jeder Streckspiegelung
Zahlen a, b, c und d, so dass die Abbildung durch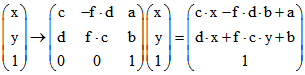
beschrieben wird, wobei f = -1 gesetzt werden muss. Für f = 1 ergibt sich eine Drehstreckung. Im Fall
f = -1 und beschreibt die Zuordnung eine Achsen- oder Gleit-Spiegelung.

Mit komplexen Zahlen , und kann man die Streckspiegelung durch
angeben, wobei die zu z konjugiert komplexe Zahl ist. Dies entspricht der
Darstellung von Drehstreckungen durch .

In den folgenden Animationen werden die vier Zahlen a, b, c und d durch einen Pfeil veranschaulicht, der
den Punkt (a ; b) mit dem Punkt (a + c ; b + d) verbindet. (c : d) ist also der zugehörige Verbindungs=
vektor. Seine Länge sei mit r bezeichnet und sein Richtungswinkel mit w. Es gilt dann also
und . Der Streckungfaktor der zum Pfeil gehörigen Abbildung stimmt mit r überein.
Streckspiegelungen bzw. Drehstreckungen werden bei diesen Pfeilen durch ein Minus- bzw. Plus-Zeichen
unterschieden. Die Pfeil-Längen und damit die Streckungsfaktoren sind alle kleiner als 1.

Die Streckspiegelung ist wie die Drehstreckung eine Ähnlichkeits-Abbildung, es werden also alle Dreiecke in
dazu ähnliche Dreiecke abgebildet, wobei allerdings die Orientierung geändert wird. Eine Reihenfolge ABC
gegen den Uhrzeigersinn geht also in eine Reihenfolge A'B'C' im Uhrzeigersinn über. Wie die Drehstreckung
hat auch die Streckspiegelung stets mindestens einen Fixpunkt. Für einen Streckungsfaktor ungleich 1, also
wenn die Streckspiegelung keine Achsenspiegelung ist, gibt es nur den Fixpunkt und nur zwei
Fixgeraden. Diese kreuzen sich senkrecht im Fixpunkt. Wenn eine Gerade g mit dem Richungswinkel w
in eine Gerade g' mit dem Richtungswinkel w' abgebildet wird, dann bleibt die Gerade h durch den Fixpunkt
F mit dem Richtungswinkel 0,5(w+w') fest. Die Streckspiegelung ist dann die Hintereinanderschaltung der
Achsenspiegelung an h und einer Streckung mit dem Zentrum F, wobei die Vertauschung dieser beiden
Abbildungen die gleiche Streckspiegelung ergibt.

Die Animation zeigt Fraktale zu einer Drehstreckung und einer Streckspiegelung , deren
zugehörige Abbildungs-Pfeile im Generator oben links gleich lang und gleich gerichtet sind. Der
Anfangspunkt des blauen Pfeils bewegt sich auf einem Kreis. Der schwarze Pfeil im Generator
verbindet die Punkte (0 ; 0) und (1 ; 0). Die Fixpunkte der beiden Abbildungen sind in jeweils
ihrer Farbe markiert, im Fraktal M mit einem weißen Rand.

Im ersten Bild in der Gleitschau nach der Animation wird dargestellt, wie sich der Fixpunkt einer
Streckspiegelung konstruieren lässt. Dabei wird benutzt, dass die Hintereinanderschaltung
von mit sich selbst eine Streckung mit gleichem Fispunkt ist. In der Zeichnung wurde auf die
Punkte (0 ; 0) und (1 ; 0) angewandt. Die Verbindungsgerade von Urbildpunkten und Bildpunkten
geht dann durch den Fixpunkt von . Die gelbe Winkelhalbierende der Verbindungsgeraden des
Fixpunktes mit den Anfangspunkten der beiden Pfeile ist Fixgerade von . Darauf werden alle Punkte
bei Anwendung von lediglich gestreckt. Dabei geht der Schnittpunkt mit dem schwarzen Startpfeil in
den Schnittpunkt mit dem roten Abbildungspfeil über.

Bild 2 der Gleitschau zeigt eine Vergrößerung des ersten Bildes der Animation mit der gelben
Fixgeraden g. Die schwarz berandeten Punkte darauf gehören zu Schnittpunkt mit dem Startpfeil und
dessen Bild bei . Durch Anwendung von klappt das Fraktal M an g um und wird dabei verkleinert.
Die Menge M, die sich aus den blauen und roten Punkten zusammensetzt, schrumpft dabei zur Menge
, die näherungsweise durch die roten Punkte allein dargestellt wird. Die erneuten Anwendungen von
lassen sich an den Spitzen des Fraktals gut verfolgen, z. B. an den Bildern des blau markierten
Fixpunktes von .

Die Bilder 3 bis 6 der Gleitschau zeigen die Wirkung eines Vorzeichen-Wechsels bei dem blauen und
dem roten Abbildungspfeil. Die Drehstreckung wird dabei in eine Streckspiegelung umgewandelt und
umgekehrt. In den Bildern 7 bis 10 sind beide Abbildungen Drehstreckungen. Es zeigt sich hierbei,
dass eine Verschiebung des blauen Abbildungspfeils nicht zu einer Veränderung der Form des Fraktals
führt. Diese Bilder gehen durch die Drehstreckungen auseinander hervor, welche die Fixpunkte
aufeinander abbilden. In den Bildern 11 bis 14 sind beide Abbildungen Streckspiegelungen.
Die auf das vierzehnte Bild folgenden (unnummerierten) Bilder sind Standbilder der Animation.

Die Animation zeigt die Wirkung von Richtungsänderungen bei zwei parallelen Abbildungs-
Pfeile, die zu einer Drehstreckung und einer Streckspiegelung gehören. Die Bilder der
folgenden Gleitschau sind Standbilder dazu.

In dieser Animation bleibt die Streckspiegelung fest, während sich der Abbildungs-Pfeil der
Drehstreckung ändert.

Hier bleibt die Drehstreckung fest und die Streckspiegelung ändert ihre Richtung.