Es lebe die Geometrie!

Inflation und Deflation bei deBruijn-Kachelungen

Auf der Seite ' Höhen und Isohypsen in Penrose-Kachelungen' wurde die Inflation bei Penrose-Kachelungen
erklärt. Die 1. Inflation einer Penrose-Kachelung aus Boot-, Kronen- und Stern-Kacheln ergibt sich
durch Verbindung jedes Kachel-Zentrums mit Zentren von Nachbar-Kacheln durch Pfeile. Jeder dieser
Pfeile kreuzt die Grenze zwischen benachbarten Kacheln K1 und K2 in einem Eckpunkt, an dem K1
bzw. K2 den Innenwinkel 144° bzw. 216° hat und der den Pfeil im goldenen Schnitt teilt. Wenn die
Seiten-Pfeile der Kacheln die Länge 1 haben, gibt die große goldene Zahl die Länge
dieser 'Flächen-Pfeile' an. Bei Stern-Kacheln zeigen die Flächen-Pfeile vom Zentrum weg, bei Boot-
Kacheln zum Zentrum hin, und bei Kronen-Kacheln zeigt nur der Pfeil auf der Symmetrie-Achse zum
Zentrum hin. Die Flächen-Pfeile einer Penrose-Kachelung sind die Rand-Pfeile ihrer 1. Inflation. Die
2. Inflation ist durch die Flächen-Pfeile der 1.Inflation gegeben. Ihre Kacheln haben als Seiten-Pfeile
die Richtungs-Pfeile der Boot-Kacheln in der Ausgangs-Kachelung.

Unter der 1. Deflation einer Penrose-Kachelung verstehen wir die Penrose-Kachelung, deren 1. Inflation
die Ausgangs-Kachelung ist. Beim Übergang zur 1. Deflation werden darum die Seiten-Pfeile durch G
geteilt, ihre Länge wird also kleiner. Bei der 2. Deflation ist gegenüber der Ausgangs-Kachelung jeder
Seiten-Pfeil p durch eine Boot-Kachel ersetzt, zu der p der Richtungs-Pfeil auf der Symmetrie-Achse ist.

Da zu jeder deBruijn-Kachelung eine Penrose-Kachelung gehört, sind die Begriffe 'Inflation' und 'Deflation'
auch für deBruijn-Kachelungen sinnvoll. Das soll im Folgenden dargestellt werden.

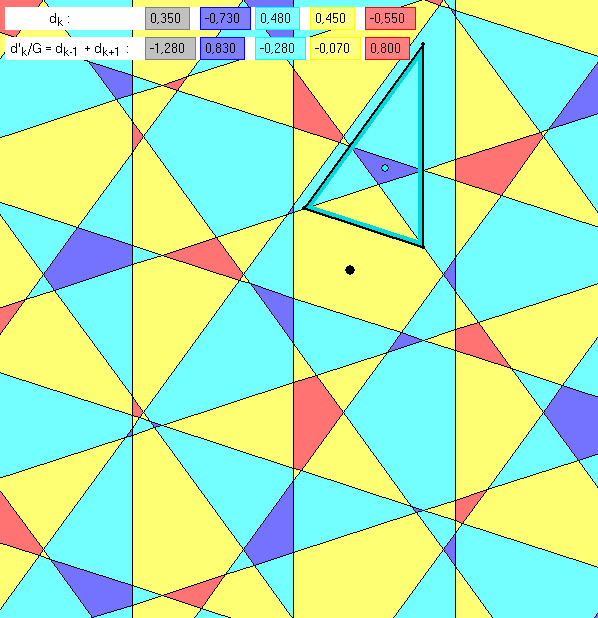
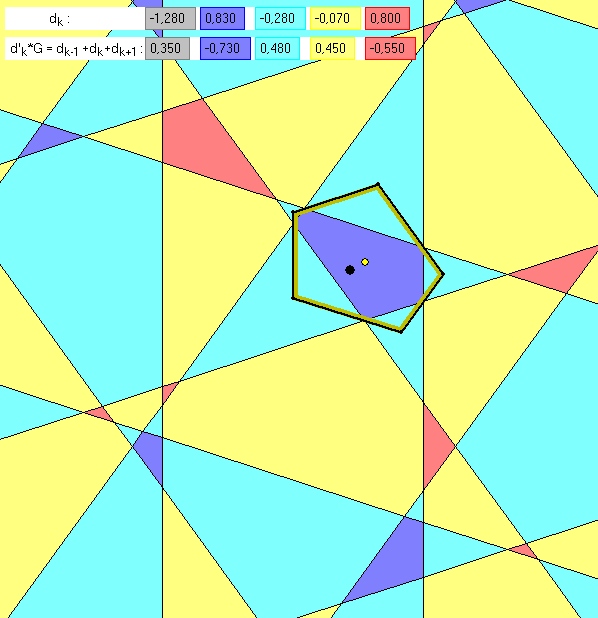
Wir bezeichnen die beiden vorangehenden Gleitschauen mit G1 und G2. Die deBruijn-Kachelung aus
farbig gefüllten Kacheln in G1 bzw. G2 sei B1 bzw. B2 genannt. B2 ist die 1. Inflation von B1, also B1
die 1. Deflation von B2. Die Abstände der Gittergeraden vom schwarz markierten Ursprung sind
jeweils in der ersten Zeile am oberen Rand der Zeichnung angegeben. Dabei ist zu beachten, dass in G2
die Längeneinheit G-mal so groß ist wie in G1 und dass in G1 und G2 die Werte für die Größen
unterschiedlich sind. In der zweiten Zeile von G1 stehen die Daten der ersten Zeile von G2, und umgekehrt.
gehört in G1 und G2 zur Ausgangs-Kachelung, deren Kacheln farbig gefüllt sind, und bezieht sich
auf die Inflarion bzw. Deflation, deren Kacheln nur mit einer Rand-Markierung ohne gefülltes Inneres
dargestellt sind. In G1 ist , und in G2 ist . Dabei wird
mit k ' modulo 5 ' gerechnet, das heißt: Für k = 0 ist k-1 = 4 und für k = 4 ist k+1 = 0.

Die Zeichnungen sollen den geometrischen Zusammenhang zwischen B1 und B2 klären. Dazu werden
Kacheln der 1. Inflation bzw. 1.Deflation nacheinander in G1 bzw. G2 mit einem farbig markierten Rand
eingefügt, so dass die Ausgangs-Kachelung möglichst wenig verdeckt wird. In G1 sind die ersten dieser
B2-Kacheln gleichschenklige Dreiecke mit einem Winkel der Größe 36° an der Spitze. Jeder Schenkel
wird durch die Spitzen eines gleichschenkligen 108°-Dreiecks von B1 zum Index 1 oder 4 im goldenen
Schnitt geteilt und halbiert dabei den Außenwinkel dieses inneren Dreiecks. Außerdem halbieren die
Schenkel-Geraden des inneren Dreiecks die Basis-Winkel der Größe 72° beim äußeren Dreieck.

Beim neunten Bild von G1 wird eine fünfeckige Kachel L hinzugefügt, die im Innern eine viereckige rote
Kachel K von B1 zum Index 4 mit den Innenwinkeln 36°, 108°, 108° 108° enthält. Eine Seite von L geht
durch den Eckpunkt von K mit dem Innenwinkeln 36° und halbiert dort den Außenwinkel. Zwei weitere
Seiten von L treffen den Schnittpunkt der Geraden zu zwei gegenüber liegenden Seiten von K, die einen
36°-Winkel einschließen, und sie halbieren ebenfalls den Außenwinkel. Die Geraden zu den Seiten von K,
die dem 36°-Winkel gegenüber liegen, halbieren 72°-Innenwinkel von L in Eckpunkten, an denen sich
eine Plus-Seite und eine Minus-Seite treffen. Durch diese Eigenschaften werden die Seiten von L vollständig
bestimmt. Das gilt analog auch für das zehnte Bild, nicht aber für das elfte mit einem neu zugefügten 7-Eck
mit zwei Paaren paralleler Seiten im Abstand G. Diese Erklärungs-Lücke soll unten auf dieser Web-Seite
geschlossen werden.

Die Seitengeraden der dunkelblauen oder roten Kacheln K von G1 bestimmen eine periodische Billard-
Bahn innerhalb der umschließenden Inflations-Kachel L, vorausgesetzt dass die Reflexion in einem
Eckpunkt von L zu einer direkten Umkehr der Bewegung der Billard-Kugel führt.

Die letzten Bilder (Nr.21, 22 und 23) von G1 zeigen die vervollständige 1. Inflation B2 vor der Ausgangs-
Kachelung B1 durch randmarkierte Kacheln, bei denen sich die Seiten zu Geraden eines Pentagrids
zusammenfügen. Das 23. Bild enthält auch dunkelblaue und rote Randmarkierungen zur Unterscheidung
von Plus-Seiten und Minus-Seiten. Zur Formulierung der daran erkennbaren geometrischen Regeln
benutzen wir Zahlen k zwischen 0 und 9 (jeweils einschließlich) zur Beschreibung von Richtungswinkeln
von Außenvektoren. Dabei verstehen wir unter einem Außen-Vektor einer Kachel einen Vektor der
Länge 1, der senkrecht zu einer Seite nach außen zeigt. Sein Richtungswinkel (gegenüber der Rechts-
Achse) ist . Dabei identifizieren wir k = 10 mit k = 0. (Diese Rechnung 'modulo 10' an Stelle der
Rechnung 'modulo 5' ist bei Geraden immer dann nötig, wenn wir eine Seite der Gerade, wie hier die
Kachel-Seite, oder eine Geraden-Richtung ausgezeichnet haben.) Wir nennen k auch 'Richtungszahl' der
zugehörigen Seitengeraden oder Seite. Die Summe der Richtungszahl-Differenzen zu aufeinander
folgenden Seiten ist stets 10. Es gibt nur die Differenzen 1, 2, 3 und 4. Sie gehören zu den Innenwinkel
144°, 108°, 72° und 36°. Genau die Richtungszahlen sind gerade, die zu Plus-Seiten gehören, bei denen
die dort angrenzende Nachbar-Kachel also einen größeren Index hat. Jede Kachel vom Index 1 oder 4
hat drei, vier oder fünf Seiten mit den Richtungszahl-Differenzen 4, 2, 4 bzw. 4, 2, 2, 2 bzw. 2, 2, 2, 2, 2.
Mit diesen Bezeichnungen gilt:

Genau die Kacheln L von B2 zum Index ind(L) = 2 (hellblau) bzw. ind(L) = 3 (gelb) enthalten eine
Kachell K von B1 zum Index ind (K) = 1 (dunkelblau) bzw. ind(K) = 4 (rot). Dabei gilt:
(*) g und h seien zwei Seitengeraden von K (möglicherweise ohne gemeinsamen Eckpunkt), die einen
36°-Winkel einschließen, deren Richtungszahlen a und b sich also um 4 unterscheiden. Dann schneiden
sich g und h auf einer Seitengerade von L, die den 144°-Nebenwinkel halbiert. Ihre Richtungszahl c
unterscheidet sich von a und b um 2, und es ist 2c = a + b.
(**) g und h seien zwei Seitengeraden von L, die in einem Eckpunkt P einen 72°-Winkel einschließen.
In P treffen dann eine Plus-Seite zur geraden Richtungszahl a und ein Minus-Seite zur ungeraden
Richtungszahl b zusammen. Dann liegt P auf einer Seitengeraden von K, die den 72°-Winkel halbiert.
Ihre Richtungswinkel-Zahl c unterscheidet sich von b um und von a um , und es
ist 2c + 5 = a + b.

Jede Kacheln L von B2 zum Index 1 und 2 ist in einer Kachel K der 1. Deflation B1 zum Index 3
bzw. 2 enthalten, aber nicht jede Kachel K enthält eine derartige Kachel L. (Zum Beispiel umfasst
keine dreieckige Kachel von B1 eine Kachel von L und manche fünfeckige auch nicht.)
Dabei gilt:
(***) g und h seien zwei Seitengeraden von L, die in einem Eckpunkt P einen 108°-Winkel einschließen
deren Richtungszahlen a und b sich also um 2 unterscheiden. Dann liegt P auf einer Seitengerade von K,
die den 108°-Nebenwinkel halbiert. Ihre Richtungszahl c unterscheidet sich von a und b um 4, und es ist
2c = a + b.

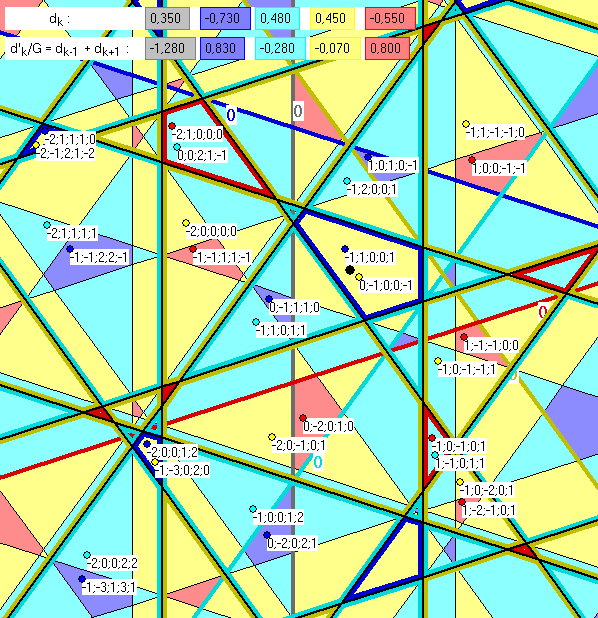
In die ersten beiden Bilder der Gleitschau sind hier 5-Tupel mit Nummern von Pentagrid-Geraden
zu Kacheln einer deBruijn-Kachelung B1 und ihrer 1. Inflation B2 eingefügt, die wir 'Frontzahlen'
nennen. Sie werden unten erklärt. Im 3. Bild ist die Inflation durch eine Deflation ersetzt. Durch die
Farbe des Punktes links oben am Tupel wird erkennbar, auf welche Kachel sie sich beziehen. Jeder
Punkt befindet sich innerhalb der Kachel, die durch das zugehörigen 5-Tupel beschrieben wird. Zwei
Tupel bilden jeweils ein Paar, von dem ein Tupel eine Kachel K aus B1 beschreibt und das andere
eine Kachel L aus B2, wobei die eine Kachel ganz in der anderen liegt. Wenn der Index der einen
Kachel 1 oder 4 ist , hat die andere den Index 3 oder 4. Die dick farbig gezeichneten Nullgeraden
der Pentagrids sind für B1 mit '0' markiert, für B2 nicht.

Die Frontzahlen f(k;K) eines Tupels stimmen für eine
Kachel K vom Index 1 oder 2 mit den Nummern der Pentagrid-Geraden überein, die von einem
Punkt im Innern von K aus in Richtung des Vektors gesehen der
Kachel am nächsten liegen. Für Kacheln vom Index 3 oder 4 sind es die Nummern, die in
Gegenrichtung von am nächsten liegen. Mit den Bezeichnungen der Seite ' de Bruijn 1' ist also
f(k;K) = j(k;K) für den Index 1 oder 2, und für den Index 3 oder 4 ist . Wir
nennen die zu einer Front-Zahl f(k;K) zugehörige Gerade 'k-te Front-Geraden von K'. Für die
Kacheln von Index 1 oder 4 sind alle Seitengeraden Front-Geraden, für die vom Index 2 oder 3
sind es die meisten, nämlich die Plus-Seitengeraden beim Index 2 und die Minus-Seitengeraden beim
Index 3. Im Fall des Index 1 oder 2 von K nennen wir eine Pentagrid-Gerade mit der Nummer 'k-te Gegengerade von K', im Fall des Index 3 oder 4 benutzen
wir diese Bezeichnung für eine Gerade mit der Nummer . ( Die Zahlen
g(k;K) sollten nicht mit den Gitter-Gerade verwechselt werden.) Der Grund dieser Bezeichnung
liegt in dem Bestreben, Bezeichnungen so zu wählen, dass Sätze über de Bruijn-Kachelungen wahr
bleiben , wenn man 'Index 1' durch 'Index 4' ersetzt und 'Index 2' durch 'Index 3'.

Satz 1 : B1 sei eine deBruijn-Kachelung mit der 1.Inflation B2. P sei ein Punkt im Innern der Kachel K
von B1 und der Kachel L von B2. Sei . Mit k wird modulo 5 gerechnet.

1. Behauptung: Sei . Aus ind(K) = 1 folgt ind(L) = 2, aus ind(K) = 4 folgt ind(L) = 3.
Außerdem gilt: und .

2. Behauptung: Sei. Aus ind(L) = 1 folgt ind(K) = 3, aus ind(L) = 4 folgt ind(K) = 2.
Außerdem gilt: und .


Beweis der 1. Behauptung: Sei P = (x ; y) und . Wir benutzen die Bezeichnungen der
Seite ' de Bruijn 1'. Danach gilt für signierten Abstände des Punktes P zur nächstgelegenen Gittergeraden
von B1 in Richtung bzw. :


Für die Summe der beiden signierten Abstände verändern sich möglicherweise die untere Grenze a und
die obere Grenze b:
.
In jedem Fall ist a = -2 eine untere Grenze und b = 0 eine obere Grenze. Für die Indizes 1 und 4 von
K ist aber eine Verschärfung möglich. Denn addiert man alle fünf signierten Abstände, so erhält man das
Produkt des Index von K mit -1. Darum ist die Summe der beiden signierten Abstände für ind(K) = 1
größer als -1, so dann man in dem Fall a = -1 setzen darf, und im Fall ind(K) = 4 ist die Summe kleiner
als -1, so dass man b = -1 setzen kann.

Da in der 1. Inflation der Maßstab mit der goldenen Zahl G vergrößert ist, gilt für den signierten Abstand
des Punktes P zur nächstgelegenen Gittergeraden von B2 in Richtung :
,
also .
Andererseits ist .Wenn man darum den mittleren Term der letzten Ungleichung von
der Summe der beiden obigen signierten Abstände abzieht, ergibt sich die Ungleichung

Da der mittlere Term eine ganze Zahl angibt, erschließt man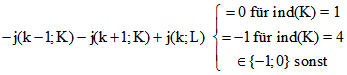

Im Fall ind(K) = 1 folgt . Da ind(K) die Summe der fünf Zahlen j(k;K)
ist und entsprechendes für ind(L) gilt, ergibt sich durch Summation der Zahlen j(k;K) der Index 2 für L.
Darum ist , und .
Im Fall ind(K) = 4 ist . Die Summation ergibt hier
. Wegen und errechnet man auch
hier .

Zum Beweis von ist zu bedenken, dass für die Summe c der
fünf Zahlen f(k;K) gilt: falls ind(K) = 1 ist, und falls ind(K) = 4. Es folgt wegen
und :
, also .

Beweis der 2. Behauptung: Für die signierten Abstände des Punktes P zur nächstgelegenen Gittergeraden
von B2 in Richtung bzw. gilt:


Durch Summation ergibt sich
.
Es ist . Für ind(L) = 1 ist a = -1 , b = 0 , und für ind(L) = 4 ist a = -2, b = -1.
Für den signierten Abstand des Punktes P zur nächstgelegenen Gittergeraden von B1 in Richtung gilt:
.
Durch Addition der Terme in den letzten beiden Ungleichungen folgt:
.
Da der mittlere Term eine ganze Zahl e ist, ist diese gleich -1 für ind(L) = 1 und -2 für ind(L) = 4.
Es ist also . Durch Summation über die fünf Zahlen k folgt
, also ind(K) = 3 für ind(L) = 1 und ind(K) = 2 für ind(L) = 4.
Darum ist in beiden Fällen .
Die Summe c der fünf Zahlen f(k;L) ist 1 falls ind(L) = 1 und -1 falls ind(L) = 4.
Wegen und ist
, also .
q.e.d.

Aus diesem Satz folgt, dass jede Kachel K mit dem Index 1 oder 4 vpllständig in einer Kachel L der
1.Inflation vom Index 2 bzw. 3 enthalten ist. Denn wenn man P innerhalb von K verschiebt, ändert sich das
Frontzahlen-Tupel von K nicht und auf Grund des Satzes auch nicht das von L. Das Frontzahlen-Tupel
bestimmt L eindeutig. Eine entsprechende Argumentation zeigt, dass jede Kachel L der 1. Inflation mit dem
Index 1 oder 4 vollständig in einer B1-Kachel K vom Index 3 bzw. 2 enthalten

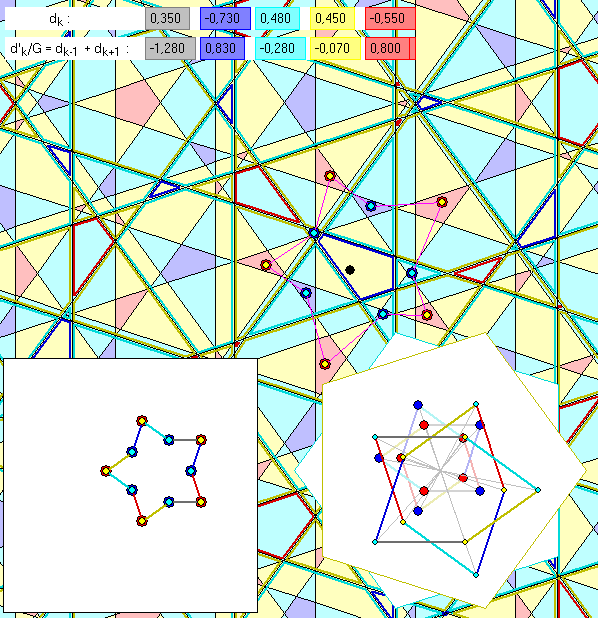
Diese Gleitschau soll den Zusammenhang zwischen der Inflation bei der deBruijn-Kachelung und der
Penrose-Kachelung klären. In den ersten sechs Bildern geht es um die Kacheln K vom Index 1 oder 4
der deBruijn-Kachelung B1, die im Innern einer Kachel L vom Index 2 bzw. 3 der 1.Inflation B2
befinden. Die mit einem roten oder dunkelblauen Punkt markierten Kacheln K von B1 haben die
Pen-Bilder bzw. Pen2-Bilder in dem Fenster unten links bzw. rechts. Die entsprechenden Punkte zu
den Kacheln L der 1. Inflation B2 sind hellblau und gelb eingezeichnet. Dabei ist zu bedenken, dass
im linken Fenster die Längeneinheit bei der Konstruktion eines Punktes Pen(L) größer ist als bei der
eines Punktes Pen(K); das Längeneinheits-Verhältnis ist nämlich die goldene Zahl G. Im rechten Fenster
wird für Pen2(K) und Pen2(L) dieselbe Längeneinheit benutzt. Es zeigt sich, dass die Bildpunkte Pen(K)
und Pen(L) zusammnefallen, während ein Punkt Pen2(L) aus dem zugehörigen Punkt Pen2(K) durch
Streckung mit dem Faktor und dem gemeinsamen Mittelpunkt M der Fünfecke
als Zentrum entsteht. Mit den Bezeichnungen der Seite de Bruijn 1 ist

und .

Beim siebenten bis elften Bild werden Kacheln L von B2 mit dem Index 1 oder 4 betrachtet. Jede
Kachel liegt im Innern einer Kachel K von B1 mit dem Index 3 bzw. 2. Auch hier fallen die Punkte
Pen(K) und Pen(L) zusammen und die Streckung mit dem Zentrum M und dem Faktor bildet
Pen2(K) in Pen2(L) ab. Folglich liegen alle Punkte Pen2(K) für Kacheln K, die ein L vom Index 1
bzw. 4 enthalten, in dem Fünfeck, das sich aus bzw. durch Streckung mit dem
Zentrum M und dem Faktor ergibt. Dies ist nach de Bruijn 2 das 5-Eck, in dem
die Pen2-Bilder der Kacheln K mit fünf Plus-Seiten liegen. Das elfte Bild zeigt, dass die Pen-Bilder
dieser Kacheln die Eckpunkte der 2. Inflation der Penrose-Kachelung zu B1 sind. Diese Eckpunkte
sind die Spitzen von Boot-Kacheln; dort treffen stets fünf Seiten zusammen. Die 2. Inflation wurde
auf der Seite de Bruijn 1 als 'Kachelung 1. Stufe' bezeichnet.

Begründung dieser Zusammenhänge:
Nach der Seite de Bruijn 1 gilt:


Bei Pen(K) und auch bei Pen2(K) darf man alle Zahlen j( k ; K) durch f( k ; K) ersetzen, da eine
Subtraktion von keine Änderung bewirkt. Entsprechendes gilt für g( k ; K).
Wenn K von B1 den Index 1 oder 4 hat und folglich eine K umschießende Kachel L von B2 den
Index 2 bzw. 3, dann folgt aus der 1. Behauptung von Satz 1:





Wegen der unterschiedlichen Längeneinheit bei der Konstruktion von Pen(K) und Pen(L) fallen darum
in der Zeichnung diese beiden Punkte zusammen. Analog schließt man beim Pen2-Bild:





Die entsprechende Argumentation mit der 2. Behauptung von Satz 1 kann auf L mit dem Index 1 oder 4
angewandt werden.

Indem man die letzte Rechnung von hinten nach vorn durchläuft, kann man begründen, dass jede Kachel
L von B2 mit dem Index 2 bzw. 3 eine Kachel K von B1 vom Index 1 bzw. 4 enthält. Denn wenn man von
den Frontzahlen f( k ; L) ausgeht, gelangt man zu der Summe der Terme ,
die zu einem Punkt von bzw. gehört, da Pen2(L) nach Voraussetzung in bzw.
liegt. Dann ist nach Satz 2 der Seite de Bruijn 1 diese Summe das Pen2-Bild einer Kachel K von
B1 zum Index 1 bzw. 4. Entsprechend zeigt man, dass jede Kachel L von B2 mit dem Index 1 bzw. 4 in
einer Kachel K von B1 zum Index 3 bzw. 2 enthalten ist.

Der vorangehende Satz1 ermöglicht durch den Beweis des folgenden Satzes auch eine Begründung für
die obigen Aussagen (*) ,(**) und (***). Mit der Bezeichnung 'Frontgerade mit der Nummer f(k;K)'
meinen wir dabei die Pentagrid-Gerade der Kachelung, zu der K gehört.

Satz 2 : B1 sei eine deBruijn-Kachelung mit der 1.Inflation B2 und . K und L seien
Kacheln von B1 bzw. B2 mit einem gemeinsamen Punkt im Innern von K und L, wobei entweder
(Fall 1) oder (Fall 2) gilt.

1. Behauptung: Die Gerade h sei im Fall 1 bzw. 2 die Frontgerade bzw. Gegengerade von L mit der
Nummer f(k;L) bzw. g(k;L). Dann haben h und die Frontgeraden von K mit den Nummern
f(k-1,K) und f(k+1,K) einen Punkt gemeinsam. Das gilt auch dann, wenn man zu f(k-1,K) bzw.
f(k+1,K) ganze Zahlen a bzw. c addiert und zu f(k;L) bzw. g(k;L) die Summe a+c.

2. Behauptung: Die Gerade h sei im Fall 1 bzw. 2 die Gegengerade bzw. Frontgerade von K mit der
Nummer g(k;K) bzw. f(k;K). Dann haben h und die Frontgeraden von L mit den Nummern
f(k-2,L) und f(k+2,L) einen Punkt gemeinsam. Das gilt auch dann, wenn man zu f(k-2,L) bzw.
f(k+2,L) ganze Zahlen a bzw. c addiert und von f(k;K) bzw. g(k;K) die Summe a+c abzieht.


Beweis der 1. Behauptung : Die Geraden mit den Gleichungen



haben genau dann einen gemeinsamen Punkt, wenn gilt: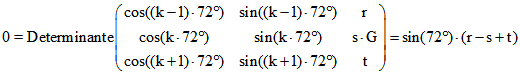



Die in der Behauptung genannten drei Geraden haben folgende Werten für r, s, t:



Darum ist Dies gilt wegen auch nach der in der Behauptung
genannten Korrektur.


Beweis der 2. Behauptung : Die Geraden mit den Gleichungen



haben genau dann einen gemeinsamen Punkt, wenn gilt: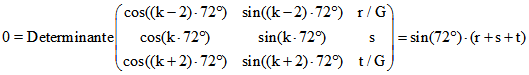



Die in der Behauptung genannten drei Geraden haben folgende Werten für r, s, t:



Darum ist . Dies gilt wegen auch nach der in der Behauptung
genannten Korrektur.
q.e.d.

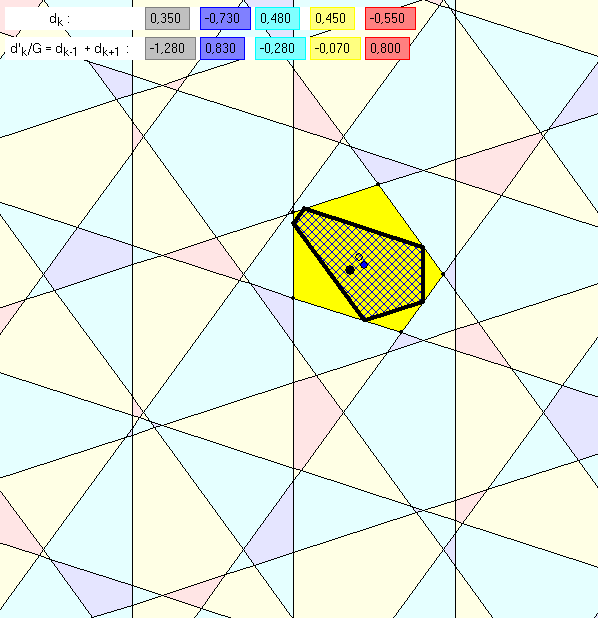
Im Zusammenhang mit den ersten beiden Gleitschauen dieser Seite wurde auf eine Lücke in
der Erklärung der geometrischen Zusammenhangs zwischen den Kacheln einer deBruijn-
Kachelung B1 und den Kacheln ihrer 1. Inflation B2 hingewiesen. Diese Lücke soll nun
geschlossen werden. In der Gleitschau gehören jeweils zwei der 21 Bilder mit Ausnahme des
21. zusammen. Das erste Bild eines Paars zeigt eine farbig gefüllt Kachel K von B1 und eine
zugeordnete kariert markierte Kachel L von B2, im zweiten Bild wird mit Hilfen von Strecken
auf Front- und Gegen-Geraden von B1 dargestellt, wie sich L geometrisch aus K ergibt. In
den ersten fünf Paaren hat K den Index 2 oder 3 und L den Index 1 bzw. 4 in den nächsten
zehn hat K den Index 1 oder 4 und L den Index 3 bzw. 2. Da 21. Bild zeigt B1 mit gefüllten
Flachen und B2 mit nur berandeten Flächen, wobei der innere dunkelblaue oder rote Rand
die Plus-Seite von den Minus-Seiten der Kacheln von B2 unterscheidet.

Da beim Index 1 bzw. 4 nur Plus- bzw. nur Minus-Seiten vorkommen, reicht bei den ersten
zehn Bildern zur Erklärung ein 5-Eck, das aus den Schnittpunkten der k-ten und der (k+1)-ten
Frontgerade von K gebildet wird. Dieses 'Front-5-Eck' wird durch weißgefüllte Eckpunkte
markiert. Wir nummerieren (modulo 5) die Seiten s0, s1,.. des Front-5-Ecks entsprechend ihrer
Farbe ( 0 für grau, 1 für dunkelblau..) und die Eckpunkte P0, P1,.. so, dass P0 Ecke zwischen
s0 und s1 ist. In den Bildern 2 und 4 der Gleitschau stimmt das Front-5-Eck mit K überein.
Wir nummerieren die schwarzen Eckpunkte Q von L und die Seiten t von L den Farben
entsprechend wie beim Front-5-Eck. Dann liegt der Punkt Qk auf der Seite s(k+3), die mit
tk und t(k+1) einen Winkel von 36° einschließt. Der Rand von L ist die eindeutig bestimmte
Billard-Bahn der Periode 5 innerhalb von K bei einem Startwinkel 36°. Die Punkte Pk,
Q(k+3) und Q(k+2) bilden ein gleichschenkliges Dreieck mit einem 36°-Basiswinkel. Wenn
(unter Missbrauch der Sprache) sk auch die Länge der zugehörigen Seite bezeichnet und uk
die Länge der Strecke zwischen P(k-1) und Q(k+2), dann ist sk = uk + u(k+1). Aus diesen
fünf Gleichungen für k = 0, ..,4 errechnet man .

In den Bildern 5 bis 10 der Gleitschau unterscheidet sich K von seinem Front-5-Eck, da sowohl
Plus- als auch Minus-Seiten vorkommen. Nicht alle Eckpunkte von L liegen dann auf den Seiten
von K. Die Summe der Eckenzahl von K und L ist aber auch hier gleich 10. Die Anwendung der
Formel für uk ist auch hier möglich, ergibt aber zum Teil negative Werte. Diese muss man dadurch
berücksichtigen, dass man den schwarzen Punkt Q(k+2) auf der k-ten Frontgeraden nicht zwischen
P(k-1) und Pk abträgt, sondern außerhalb von sk. Das 5-Eck der Qk hat dann auch hier die
Eigenschaft, dass die Punkte Pk, Q(k+3) und Q(k+2) ein gleichschenkliges Dreieck mit einem
36°-Basiswinkel bilden. Das 'Billard-5-Eck' der Qk verläuft jetzt nicht mehr innerhalb von K,
sondern schneidet den Rand in Eckpunkten, an denen eine Plus-Seite auf eine Minus-Seite trifft.
Dort wird der Innenwinkel halbiert. Der Begriff 'Billard-Bahn' lässt sich rechtfertigen, wenn man
als Reflexion in diesen Eckpunkten die Bewegungs-Umkehr ansieht. Das Seiten des Billard-5-Eck
schneidet sich selbst. Dadurch gibt es sowohl Punkte mit der Umlaufzahl 1 als auch -1, die also bei
einem Umlauf des Billard-5-Ecks in Richtung der Farbfolge grau, dunkelblau, hellblau, gelb und
rot links herum bzw. rechts herum umlaufen werden. Das Innere von L ist die Menge der Punkte
mit der Umlaufzahl 1. Das Billard-5-Eck ist das Front-5-Eck von L.

In den Bildern 11 bis 20 der Gleitschau hat K den Index 1 oder 4 und die zu K gehörigen Kachel K
den Index 2 bzw. 3. Hier ist es sinnvoller, statt des Front-5-Ecks von K das zugehörige Pentagramm
zu betrachten, das wir 'Front-5-Stern' nennen. Die Innenwinkel-Größen sind hier nicht 108° wie beim
Front-5-Eck, sondern 36°. Bild 11 zeigt, dass L das 5-Eck der Schnittpunkte von aufeinanderfolgenden
Winkelhalbierenden der Außen-Winkel des Front-5-Sterns ist. Dies ist das Front-5-Eck von L. Der
Front-5-Stern von K zeigt hierin die periodische Billard-Bahn mit der Periode 5 und dem Startwinkel
72°. In Bild 12 stimmt L mit seinem Front-5-Eck überein. Dort ist zusätzlich mit dickem farbigen
Stift ein umschließendes 5-Eck eingezeichnet, das für die Erklärung von L eigentlich überflüssig ist.
Seine Eckpunkte sind die Schnittpunkte aufeinanderfolgender Gegen-Geraden von K. Wir nennen es
'Gegen-5-Eck'. Die dazu eingezeichnete 5-periodische Billard-Bahn zum Startwinkel 36° hat hier keine
Funktion, da sie das Front-5-Eck von L nicht schneidet. Sie ist das Gegen-Fünfeck von L. Seine
Bedeutung wird im Bild 14 klar. Dort schneidet diese Bahn einen Teil vom Innern des Front-5-Ecks
von L ab, so dass das 6-Eck von L übrig bleibt. Auch bei den Kacheln K in den Bildern 15 bis 20 gilt:

M1 sei die Menge der Punkte, die bei einem Umlauf um das Front-5-Eck von L in Richtung der
Farbfolge grau, dunkelblau, hellblau, gelb, rot die Umlaufzahl 1 haben. M2 sei die entsprechende
Menge der Punkte des Gegen-5-Ecks. Dann ist L die Schnittmenge von M1 und M2.

Die Animation zeigt auf einer Spiralspur Front-5-Ecke und Gegen-5-Ecke, die ihre schwarz umrandeten
farbig karierten Schnittmengen zurücklassen. Diese sind Kacheln der 1. Inflation B2 der zugrundeliegenden
deBruijn-Kachelung B1 aus farbig gefüllten Flächen. Dasjeweilige dick farbig gezeichnete Front-5-Eck
oder Gegen-5-Eck bezieht sich hier auf eine Kachel L von B2 und entspricht in der vorherigen Gleitschau
einem dünn farbig gezeichneten Polygon. Dort bezog sich das dick gezeichnete Front5-Eck oder
Gegen-5-Eck auf eine Kachel K von B1.