Es lebe die Geometrie!

Stereografische Projektion der Zylinder-Ellipsen auf Parabeln einer Ebene

Die stereografische Projektion ist eine Abbildung von Punkten einer Quadrik, also zum Beispiel der Oberfläche
eines Zylinders, einer Kugel, eines Ellipsoids oder eines Hyperboloids, auf Punkte einer Bildebene BE. Dabei
gibt es auf der Quadrik einen ausgewählten Punkt Z mit folgender Eigenschaft:

Jeder abgebildete Punkt P ist mit seinem Bildpunkt P' und mit Z kollinear,
das heißt, dass P, P' und Z gemeinsam auf einer Geraden liegen.

Das Projektionszentrum Z darf nicht auf der Bildebene BE liegen. Jeder Punkt von BE kommt als Bildpunkt vor,
aber nicht zu jedem Punkt der Quadrik gibt es einen Bildpunkt, denn dem Projektionszentrum Z ist kein
Bildpunkt zugeordnet. Die Menge der Punkte, die einen Bildpunkt haben, nennen wir Q.

Meist nimmt man für BE eine Symmetrie- oder eine Tangential-Ebene der Quadrik. Wenn M die Schnittmenge
einer Ebene mit der Quadrik ist, dann hat die Menge M' der Bildpunkte P' zu Punkten P in M besondere
Eigenschaften. Bei der Kugelfläche ist M eine Kreis und M' ein Kreis oder eine Gerade (siehe die Seite
' Stereographische Projektion'). Q besteht dann aus allen Kugelflächen-Punkten außer Z. Wenn im Fall der
Zylinder-Fläche die Bildebene BE parallel zur Zylinder-Achse verläuft, die Schnittebene aber nicht, dann ist
M eine Ellipse und M' eine Parabel oder eine Gerade. Q enthält dann alle Punkte der Zylinder-Fläche, deren
Verbindungsgerade mit Z nicht parallel zur Zylinder-Achse ist.

Wir benutzen im Folgenden den Zylinder über dem Einheitskreis um den Ursprung in der xy-Ebene und wählen
als Projektions-Zentrum Z den hinteren Schnittpunkt der x-Achse mit der Zylinder-Fläche. Das Quadrupel zu
Z ist also (-1;0;0;1). BE sei die Tangential-Ebene im vorderen Schnittpunkt der x-Achse. E hat die Gleichung
x = 1 und das Quadrupel [1;0;0;-1].

Die Animation zeigt die stereografische Abbildung der roten Zylinder-Ellipse auf die rote Parabel in der
Tangential-Ebene BE. Die blaue und grüne Parabel ergeben sich nach dem gleichen Verfahren. Zusätzlich
sind die Zykeln eingezeichnet, die sich mit der Blaschke-Abbildung aus den Ellipsen ergeben. Die Pfeile
an den Zykeln gehören zu den Pfeilen, die einen Punkt der z-Achse mit einem Schnittpunkt zweier
Zylinder-Ellipsen verbinden. Jeder dieser Zykel-Pfeile hat einen gleichgerichteten Partner an einem
anderen Zykel mit einer gemeinsamen Tangenten-Geraden. Die Zykeln kann man sich als Schnitt-Kurven
der xy-Ebene mit einem Kegel vorstellen, dessen Böschungslinien mit der xy-Ebene einen Winkel von
45° einschließen. Die drei Kegelspitzen bilden ein Dreieck, zu dem oben links im Bild eine verkleinerte
Version gezeichnet ist.

Jede Ellipse hat mit ihrer Bild-Parabel genau einen Punkt gemeinsam, der auf der Parallelen zur Zylinder-
Achse durch den Punkt mit dem Quadrupel (1; 0;0;1) liegt. In diesem Punkt berühren sich die beiden
Kurven, sie haben also dort eine gemeinsame Tangente. Wenn P ein Zylinder-Punkt mit dem Quadrupel
ist, dann hat der Bildpunkt P' in BE das Quadrupel 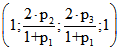. Dabei ist
. Wenn die Ebene E einer Zylinder-Ellipse das Quadrupel hat, dann wird die
Bild-Parabel durch die Gleichung beschrieben. Dabei legt man
in BE ein klokales Koordinatensystem mit Achsen parallel zur raumlichen y- bzw. z-Achse zugrunde.
Die Gleichung kann man auch in der Form 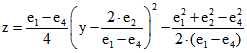schreiben, oder
in der Form , wenn der kleine Kreis das Zeichen für das
(übliche) innere Produkt ist.

In den Standbildern der Gleitschau im Anschluss an die Animation sind in dem Dreieck oben links die
Werte d(P,Q) des nicht-euklidischen Abstands-Maßes der Eckpunkte angegeben. Für die Spitzen A
und B des Kegels zum roten bzw. blauen Zykel mit dem Quadrupel bzw.
berechnet man diesen Wert durch .

D und E seien die Ebenen der Ellipsen, zu denen A und B gehören, und und
ihre Quadrupel (wobei hier der Buchstabe 'd' für das Maß von dem für das Quadrupel unterschieden werden
muss.) Dann ist auf Grund des auf der Seite ' Nullpolarität' dargestellten Zusammenhangs ,
und . Zum Punkt B gehört also die Parabel


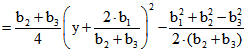
Das dem Abstands-Maß der Kegelspitzen entsprechende Abstandsmaß der Zylinder-Ellipsen ist . Wenn also d bzw. e die Quadrupel von D bzw. E sind, die zu
den Punkten A bzw. B gehören, dann ist der (d;e) zugeordnete Formwert gleich d(A;B). Wenn die zu D
und E gehörigen Zykeln eine gemeinsame Tangente haben, ist der zugehörige Maß-Wert das Quadrat des
euklidischen Abstands der Berührpunkte der Tangente. (Siehe dazu die Seite ' Spiegelungen 1')

Wenn man die Parabel, die zu A und D bzw. B und E gehört, mit Hilfe des Vorzahlen-Tripels
bzw. beschreibt, weil die Parabelfunktion bzw.
ist, dann ist .

Um die Orthogonalität im Raum der Kegelspitzen zu beschreiben, musste man ein Dreieck ABC mit einem
rechten Winkel bei z. B. C betrachten, da sich dafür der Satz von Pythagoras direkt übertragen ließ. Aus
d(a;b) = d(b;c) + d(c;a) folgt dann für die Verbindungsvektoren von C nach A bzw.
von C nach B: .
Wenn man für die Vorzeichen-Tripel j, k und der zu A, B und C gehörigen Parabeln entsprechende
Verbindungsvektoren und einführt, sieht die
Verknüpfung zur Beschreibung der Orthogonalität anders aus. Es gilt nämlich

.
Wegen der Übertragung des Satzes von Pythagoras für Kegelspitzen ist dieser Term genau dann Null,
wenn die Verbindungsvektoren v und w orthogonal sind. Darum ist die adäquate Verküpfung für
die Parabeln durch gegeben.


Die Maßzahlen in den Zeichnungen der Gleitschau verdeutlichen folgenden Zusammenhang:

Im Fall d(A;B) > 0 haben sowohl die D und E zwei gemeinsame Punkte, und auch
die zugehörigen Parabeln; die zugehörigen Zykeln haben zwei gemeinsame Tangenten.

Im Fall d(A;B) = 0 berühren sich D und E und auch die zugehörigen Parabeln und Zykeln.

Im Fall d(A;B) < 0 haben D und E und ihre Parabeln keinen Schnittpunkt und die Zykeln keine
gemeinsame Tangente.

Das Bild einer Zylinder-Ellipse ist eine Gerade, wenn der zugehörige Zykel die x-Achse berührt.

Wenn das Dreieck ABC einen (nicht-euklidisch) rechten Winkel bei C hat, dann gilt der Satz von
Pythagoras, nämlich d(a;b) = d(b;c) + d(c;a).

Im Folgenden soll geklärt werden, welche geometrische Bedeutung die Maßzahlen für die Parabeln haben.

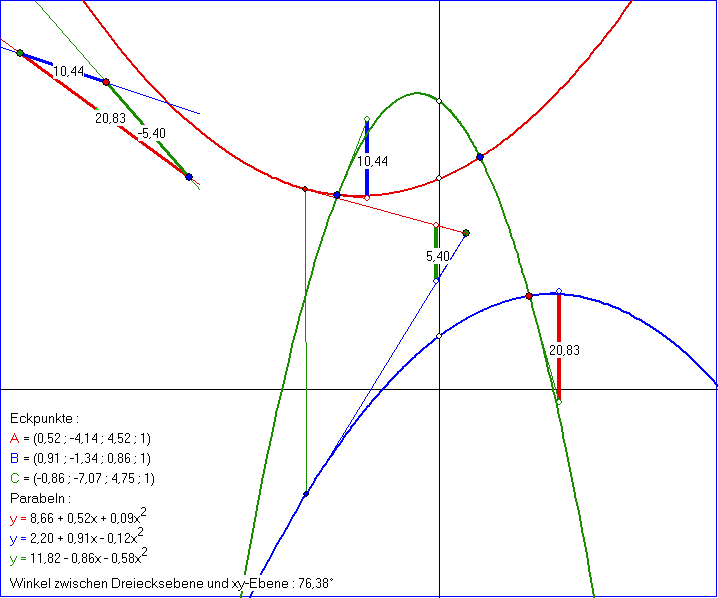
Die Gleitschau zeigt den Zusammenhang zwischen den Seitenmaßen des Dreiecks ABC und
den Steigungen der zu den Eckpunkten gehörigen Parabeln, die sich bei stereographischer
Projektion der zu den Eckpunkten gehörigen Zylinder-Ellipsen ergeben. Beim Dreieck sind
die Maßzahlen d(A;B), d(B;C) und d(C;A) angegeben. Da d(A;B) <0 ist, schneiden sich die
rote und die blaue Parabel nicht. Bei den schneidenden Parabeln sind d(B;C) bzw. d(C;A)
die Quadrate der Differenzen der Steigungen in einem Schnittpunkten. Da die Differenzen der
Steigungen sich in den beiden Schnittpunkten nur im Vorzeichen unterscheiden, sind die Quadrate
für beide Schnittpunkte gleich. Bemerkenwert ist dabei, dass die Steigung bei den Parabeln eine
Größe ist, die sich im Graf euklidisch messen lässt, was bei den Dreieck-Seiten höchstens über
den Tangentialabstand der zu den Eckpunkten gehörigen Zykeln möglich ist.

Auch d(A;B) kann als Quadrat von Steigungs-Differenzen gedeutet werden, wobei allerdings die
Steigungen an einer Stelle betrachtet werden, die keine Schnittstelle ist. ist die gemeinsame
Berührstelle der beiden Tangenten an die rote und blaue Parabel durch den grünen Punkt ,
den wir 'Potenz-Mitte' der beiden Parabeln nennen. Für schneidende Parabeln ist die Potenz-Mitte
der Mittelpunkt ihrer Schnittpunkte. Die Menge der Punkte P mit der Eigenschaft, dass die beiden
Tangenten durch P an die roten und die blaue Parabel die gleiche Berührstelle haben, ist die
Punktmenge der zwischen den beiden Parabeln gezeichneten grünen 'Potenz-Gerade' g der beiden
Parabeln. ist der Schnittpunkt von g mit der Geraden h, die parallel zur Hoch-Achse verläuft
und die rote und die blaue Parabel in Punkten U und V schneidet, in denen die Tangenten parallel
sind. Für die Vorzahlen bzw. von im Term der blauen bzw. der roten Parabel
gilt dann: Ihr mit -1 multipliziertes Verhältnis gibt das Verhältnis an, in dem die Strecke UV teilt.
Wenn dieser Wert negativ ist, liegt die Potenz-Mitte außerhalb der Strecke UV. Die Parallele h zur
Hoch-Achse durch die Potenz-Mitte nennen wir auch 'Achse' oder 'Zentrale' der beiden Parabeln.
Wenn man die Potenz-Mitte an der Mitte der Strecke UV euklidisch spiegelt, erhält man einen
weiteren ausgezeichneten Punkt. Er ist nämlich der Schnittpunkt von den Verbindungsgeraden der
Brennpunkte und der Extrempunkte der Parabeln zu A und B.

Die Parallelität der Tangenten in den Punkten U und V bedeutet für die zu A und B gehörigen Ellipsen,
dass die Tangenten an die Urbilder von U und V sich auf einer Parallelen zu den Tangenten durch das
Projektionszentrum Z schneiden. Ein Bild dazu findet man in der Gleitschau.

Im Sonderfall, in dem eine der Parabeln durch eine Gerade j ersetzt wird, ist diese selbst die zugehörige
Potenz-Gerade. Die Achse ist dann die Parallele zur Hoch-Achse, in deren Schnittpunkt mit der Parabel
die Tangente parallel zu j ist. Die Potenz-Mitte ist der Schnittpunkt der Achse mit j.

Die drei Potenzgeraden zu den drei Parabel-Paaren, die man den Dreieck-Seiten AB, BC und CA
zuordnen kann, schneiden sich in dem 'Potenz-Zentrum' der drei Parabeln. Dieser Punkt liegt mit dem
Schnittpunkt der drei Ellipsen-Ebenen und dem Zentrum Z der stereographischen Projektion auf einer
Geraden.

Der Begriff 'Potenz' wird für Parabeln ähnlich definiert wie für Kreise, allerdings mit einem anderen
Abstands-Maß. Zu einem Kreis K ist die Potenz eines Punktes P folgendermaßen definiert:

R und S seien Schnittpunkte einer Geraden k durch P mit dem Kreis, die bei einer Tangente
zusammenfallen. Dann ist die Potenz von P zu K das Produkt der Abstände von P zu R und S,
im Fall, dass P zwischen R und S liegt, noch multipliziert mit -1.

Die Potenz eines Punktes P, der auf der Rechts-Achse die Koordinate p hat, zu einer Parabel K
definieren wir folgendermaßen:

r und s seien Schnittstellen einer Geraden k durch P mit der Parabel, die bei einer Tangente
zusammenfallen. Dann ist die Potenz von P zu K gleich .

Sowohl beim Kreis, als auch bei der Parabel ist diese Definition unabhängig von der Wahl von k,
es ergibt sich also für alle Schnittgeraden der gleiche Wert. Für Punkte der Potenzgeraden zweier
Kreise bzw. Parabeln ist dieser Wert für beide Kurven gleich. Für das Potenz-Zentrum dreier
Kreise bzw. Parabeln ist die Potenz zu allen drei Kurven gleich.

sei der Term einer Parabel oder Geraden mit der Gleichung z = j(y).
Dann ist der Term der Potenz-Geraden der verschiedenen Parabeln mit den Termen j(y) und k(y)
der Term in der Menge , für den die Vorzahl von gleich
Null ist. Dies gilt auch, wenn eine der beiden Parabeln durch eine Gerade g ersetzt wird.

Wenn j(y) der Term einer Parabel ist, gibt der Term die Potenz für einen Punkt P in der
Bildebene x = 1 der stereographischen Projektion mit dem Quadrupel an.

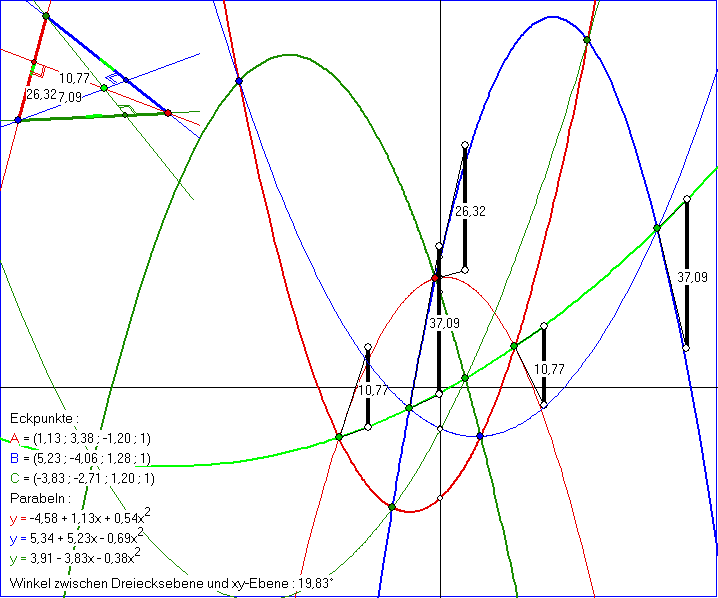
Die Gleitschau zeigt die Übertragung des Satzes über den Schnittpunkt der Höhen bzw. der
Mittelsenkrechten in einem Dreieck des Raums der Kegelspitzen in das Parabel-Modell. Punkten
in der Geometrie der Kegelspitzen entsprechen Parabeln im Parabel-Modell. Verbindungsgeraden
entsprechen Parabel-Büschel. Wenn z. B. zu den Punkten A und B die Parabeln mit den Termen
j(y) und k(y) gehören, dann gehört zu dem Punkt P der Geraden AB mit dem Quadrupel
der Parabel-Term . Dabei ist r eine
reelle Zahl. Wenn die Parabeln zu A und B sich schneiden, dann geht die Parabel zu P durch
beide Schnittpunkte. Die Achsen und die Potenz-Geraden von je zwei der drei Parabeln zu
A, B und P stimmen überein.

Leider kann die Orthogonalität von Geraden im Raum der Kegelspitzen nicht in befriedigender
Deutlichkeit im Parabel-Modell geometrisch dargestellen. Ein Notbehelf ist es, zu zwei orthogonalen
Geraden g und h den Schnittpunkt S und zwei Punkte P und Q auf g bzw. h zu betrachten. PQS
bildet dann ein rechtwinkliges Dreieck, auf das sich der Satz von Pythagoras übertragen lässt. Die
Orthogonalität zeigt sich dann daran, dass bei Quadraten der Differenzen von Steigungen die Summe
zweier Werte mit einem dritten Wert übereinstimmt.