Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Begründung
Geometrie 2 > Gleichdick
Darstellung eines Gleichdicks
mit Hilfe einer Drehpunktfunktion
-->Figuren mit konstanter Breite
https://www.vivat-geo.de/Pdf-Dateien/Gleichdick.pdf
Es sollen auf dieser Seite die mathematischen Grundlagen der Darstellung der Randkurve eines Gleichdicks
als Evolvente einer Drehpunktkurve gelegt werden.
Unter einer ebenen konvexen Menge M verstehen wir eine Punktmenge im ![]() , die mit je zwei Punkten auch
, die mit je zwei Punkten auch
alle Punkte der Verbindungsstrecke enthält. Eine 'Stützgerade ![]() von M zum Richtungswinkel
von M zum Richtungswinkel ![]() ' sei eine
' sei eine
orientierte Gerade mit dem Richtungswinkel ![]() , die mit dem Rand von M mindestens einen Punkt
, die mit dem Rand von M mindestens einen Punkt
gemeinsam hat, bei der aber kein Punkt von M auf der rechten Seite der Geraden liegt. Der Abstand der
parallelen Stützgeraden ![]() und
und ![]() wird die 'Breite
wird die 'Breite ![]() von M bei
von M bei ![]() ' genannt. Eine konvexe
' genannt. Eine konvexe
Menge heißt 'beschränkt', wenn es zu jedem Richtungswinkel eine Stützgerade gibt. Eine beschränkte konvexe
Menge heißt 'Gleichdick', wenn die Breiten für alle Richtungswinkel gleich sind.
Auf den Seiten der Ebene 'Gleichdick' benutzen wir zur Darstellung der Randkurve eines Gleichdicks eine
Evolvente einer Drehpunktkurve zu einer Drehpunktfunktion f. (An anderer Stelle wurden f selbst benutzt.)
Definition : Eine Funktion f von der Menge der reellen Zahlen in sich heißt 1-periodische Drehpunktfunktion,
wenn gilt:
1. ![]() für alle
für alle ![]() ,
,
2. f hat im Intervall ![]() beschränkte Variation, d. h. dass f in diesem Intervall
beschränkte Variation, d. h. dass f in diesem Intervall
als Differenz zweier monotoner Funktionen dargestellt werden kann, und
3. 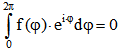 .
.
Wegen 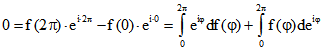
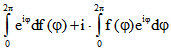
ist die dritte Eigenschaft äquivalent mit 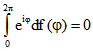 .
.
Eine zu f gehörige Drehpunktkurve ist die Kurve 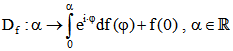 in der komplexen
in der komplexen
Ebene oder eine Kurve, die daraus durch Verschiebung entsteht. Wenn f differenzierbar ist, dann ist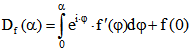 . Im Fall von Sprungstellen setzen wir auf dieser Seite voraus, dass dort
. Im Fall von Sprungstellen setzen wir auf dieser Seite voraus, dass dort
der Funktionswert von f der Mittelwert des links- und rechtsseitigen Limes ist. Wenn f für diese Normierung
geändert werden muss, ändert die Drehpunktkurve sich dadurch nicht. Sie ändert sich in der Form auch nicht,
wenn zu den Funktionswerten von f eine Konstante addiert wird.
Die Evolvente dieser Drehpunktkurve zum Parameterwert s ist die Kurve
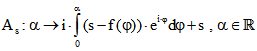 , die wir 's-Kurve' nennen.
, die wir 's-Kurve' nennen.
Wenn s obere Schranke von f ist, also alle Funktionswerte von f kleinergleich s sind, dann liegen alle Punkte
des Graphen von ![]() auf dem Rand der konvexen Hülle M des Graphen. (M ist die kleinste konvexe Menge,
auf dem Rand der konvexen Hülle M des Graphen. (M ist die kleinste konvexe Menge,
die den Graphen enthält.) Die Breite von M bei ![]() ist
ist 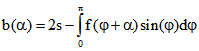 .
.
Siehe dazu http://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf.
Als Definitionsbereich von f wird auf dieser Seite stets die ganze Menge der reellen Zahlen gewählt, weil
dies die Darstellung des Zusammenhangs im folgenden Satz erleichtert. Bei Anwendungen des Satzes auf den
folgenden Seiten ist der Definitionsbereich meist eingeschränkt definiert, ist dann aber periodisch fortsetzbar.
Satz : f sei eine 1-periodische Drehpunktfunktion. s und c seien reelle Zahlen.
Dann sind für die Evolvente ![]() der Drehpunktkurve von f folgende Aussagen äquivalent:
der Drehpunktkurve von f folgende Aussagen äquivalent:
(1) Für alle ![]() gilt:
gilt: ![]()
(2) Für alle ![]() gilt::
gilt:: ![]() .
.
Wenn (1) oder (2) gilt, dann ist ![]() der Mittelwert von f, also
der Mittelwert von f, also ![]() .
.
Beweis: Es sei zunächst (1) vorausgesetzt. Sei ![]() und
und ![]() . Dann ist
. Dann ist
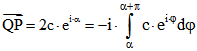 . Andererseits ist
. Andererseits ist
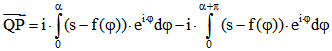
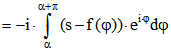
Daraus folgt 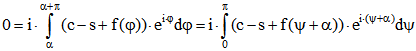
also auch 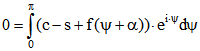 für alle
für alle ![]() .
.
Da f in einem Perioden-Intervall beschränkte Variation hat, gibt es eine Fourier-Reihe![]() , die gegen
, die gegen ![]() konvergiert (siehe dazu
konvergiert (siehe dazu
https://projecteuclid.org/euclid.pja/1195521140). ![]() ist dabei der Mittelwert von f.
ist dabei der Mittelwert von f.
Wenn man im Term 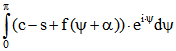 für f die Fourier-Reihe einsetzt, treten die
für f die Fourier-Reihe einsetzt, treten die
Integrale 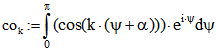 und
und 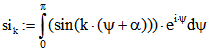 auf.
auf.
Für ungerade k ergibt sich bei beiden Integralen Null. Für geradzahlige k > 0 ist![]() und
und ![]() .
.
Die Einsetzung führt also zur Gleichung![]()
Bei Trennung der Realteile und Imaginärteile folgt![]() und
und![]()
Da die Terme auf der rechten Seite für alle Null ergeben, folgt aus der parsevalschen Gleichung,
dass alle Koeffizienten Null sein müssen. Darum gilt ![]() für alle j > 0 und
für alle j > 0 und ![]() .
.
In der Fourier-Reihe von f gibt es also außer dem konstanten Glied keinen Summanden mit einem
geraden k. Wegen ![]() für ungerade k
für ungerade k
ist darum ![]() .
.
Sei nun umgekehrt (2) vorausgesetzt.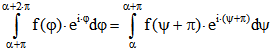
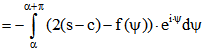 .
.
Da ![]() die Periode von f ist gilt
die Periode von f ist gilt 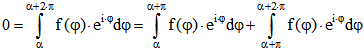
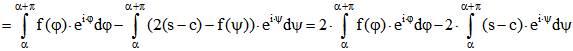 .
.
Folglich ist 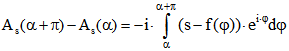
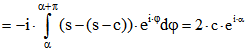
q.e.d.
1. Folgerung: Wenn ![]() Randkurve eines Gleichdicks M mit der Breite 2c ist, dann folgt
Randkurve eines Gleichdicks M mit der Breite 2c ist, dann folgt![]() für alle
für alle ![]() .
.
Denn in M gibt es keine zwei Punkte, deren Abstand größer als 2c ist. Wenn darum P ein Punkt
von M auf der Stützgeraden ![]() ist und Q ein Punkt von M auf
ist und Q ein Punkt von M auf ![]() , dann ist der Abstand
, dann ist der Abstand
dieser beiden Punkte gleich 2c und die Verbindungsstrecke steht senkrecht auf den Stützgeraden.
Darum hat der Verbindungsvektor den Richtungswinkel ![]() und
und ![]() .
.
Bei der Untersuchung von Gleichdicken mit Hilfe einer Drehpunktfunktion f ist es sinnvoll, sich auf
Funktionen mit dem Mittelwert Null zu beschränken. Denn bei einer Verschiebung des Graphen von f
in Richtung der Hochachse ändert sich die Drehpunktkurve in ihrer Form nicht, und bei einem Mittelwert
Null vereinfacht sich die in der 1. Folgerung genannte Gleichung zu ![]() für alle
für alle ![]() .
.
2. Folgerung: f sei eine Drehpunktfunktion mit ![]() für alle
für alle ![]() und s eine obere
und s eine obere
Schranke von f. Dann ist der Mittelwert von f gleich Null, und die s-Kurve ist Rand eines Gleichdicks
mit der Breite 2s. Für alle ![]() ist
ist ![]() .
.
Aus ![]() folgt nämlich
folgt nämlich ![]() , so dass der Mittelwert von f gleich Null
, so dass der Mittelwert von f gleich Null
ist. Die Eigenschaft (2) ist damit erfüllt, also auch (1). Da s obere Schranke ist, berandet ![]() eine
eine
konvexe Menge M, die für alle ![]() zwischen den Stützgeraden
zwischen den Stützgeraden ![]() und
und ![]() liegt, welche
liegt, welche
nach (1) den Abstand 2s haben. Darum ist M ein Gleichdick mit der Breite 2s. Außerdem ist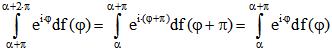 , also
, also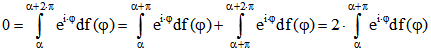 und darum
und darum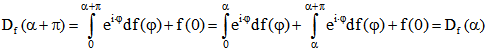 .
.
Untermenü