Es lebe die Geometrie!

Bogenlängen bei k-Zykloiden

Die Bogenlänge kann mit Hilfe der Geschwindigkeit beim Durchlauf der Zykloide berechnet werden oder mit
Hilfe einer zur k-Zykloide gehörigen Drehpunktfunktion. Beim ersten Verfahren geht man von der Funktion
mit aus, deren Ableitung
den Vektor der Geschwindigkeit im Zykloidenpunkt in komplexer Form angibt, wenn proportional
zur Zeit wächst. ist die Differenz zweier Einheitsvektoren mit den Richtungswinkeln und
, die also einen Winkel der Größe einschließen. Die Länge dieses Differenzvektors ist darum
und der Betrag des Geschwindigkeitsvektors . Die
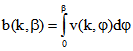Bogenlänge zwischen den Punkten und ist dann durch gegeben. Im
Intervall 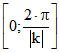ist . Ein ganzer Zykloiden-Bogen hat darum die
Länge 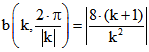. Für das auf 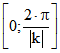folgende Intervall 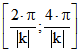ist diese Länge zu
berücksichtigen, so dass hier gilt. Für alle ist 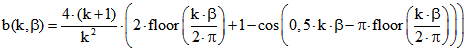(ohne Betrags-Stiche!)
ein Term zur Beschreibung der Bogenlänge zwischen den Zykloiden-Punkten und .


Eine Drehpunktfunktion ist eine reellwertige Funktion des Richtungswinkels einer Tangente,
die man sich an einer Kurve abrollend vorstellen kann, und für die der Funktionswert den Ort des
Berührpunktes in einem eindimensionalen Koordinatensystem auf der Tangente angibt. (Siehe auch
http://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.) Eine für die k-Zykloide geeignete Funktion
ist die Drehpunktfunktion . In der komplexen Ebene ist dann die
Kurve der Drehpunkte durch 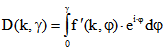gegeben, wobei die Ableitung von f nach benutzt
wird. Der Zusammenhang mit der k-Zykloide zeigt sich daran, dass der Funktionsterm dieser Kurve mit
übereinstimmt. An der Stelle der Variablen steht hier , weil
der Richtungswinkel der Tangente ist. Das Integral 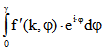ist Grenzwert einer Summe von Termen
der Form , wobei eine kleine Weglänge in Richtung der Tangente und
einen Einheitsvektor in dieser Richtung beschreibt. Darum ist die Bogenlänge zwischen den Punkten
und gleich 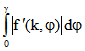. Wenn f im Intervall monoton ist, wird folglich die Bogenlänge durch
gegeben.

Zur Darstellung der Steiner-Zykloide wurde hier die Drehpunktfunktion benutzt.
Der bewegte Pfeil verbindet auf der Tangente die Punkte mit den Koordinaten -1 mit +1. Die Länge des
durch Punkte markierten Bogens stimmt mit der Länge der Strecke zwischen dem gelben Berührpunkt und
dem ebenfalls gelben Punkt auf der Spitzen-Evolvente überein. Im Graphen der Drehpunktfunktion ist die
Länge entsprechend durch eine schwarze Strecke markiert. Die Länge eines Zykloidenbogens beträgt 16/9.

Für die Darstellung der Nephroide (2-Zykloide) wurde die Drehpunktfunktion
benutzt. Die Länge eines Zykloidenbogens ist 6.