Es lebe die Geometrie!

Schraubungen im elliptischen projektiv-metrischen Raum

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

Im dreidimensionalen projektiven Raum beschreiben wir Punkte und Ebenen durch Quadrupel reeller Zahlen,
die nicht alle gleich Null sind. Für Punkte benutzen wir runde Klammern und für Ebenen eckige. Wenn man
ein Quadrupel mit einer Zahl r ungleich Null multipliziert, beschreibt das Ergebnis-Quadrupel
denselben Punkt. Entsprechendes gilt für Ebenen-Quadrupel. Wenn ein Punkt im
dreidimensionalen affinen Raum durch das Koordinalen-Tripel gegeben ist, gehört dazu das
Koordinaten-Quadrupel . Ein Punkte zu gehört genau dann zu der Ebene
mit dem Quadrupel , wenn
ist. Die Ebene mit dem Quadrupel [0 ; 0 ; 0 ; 1] nennen wir 'unendlich ferne Ebene'. Die Punkte, die nicht
mit dieser Ebene inzidieren, bilden den affinen Raum.

Der projektive Raum wird zu einem metrischen Raum durch Angabe einer symmetrischen Bilinearform für die
Ebenen-Quadrupel. Als 'elliptisch' bezeichnen wir hier den Raum, wenn die Bilinearform mit einer konstanten
reellen Zahl k > 0 durch gegeben ist. Im Fall k = 0 nennen wir
den Raum 'euklidisch' und im Fall k < 0 'hyperbolisch' (siehe auch die Seiten 'euklidische Raumgeraden' >
' Höhen im 6-Rechteck' und 'hyperbolische Raumgeraden' > ' Orthogonalität').Wir nennen die zu d und e
gehörigen Ebenen D und E 'elliptisch orthogonal', wenn f(d;e) = 0 gilt. Der Punkt P mit dem Quadrupel
hat die Eigenschaft, dass alle Ebenen durch P elliptisch orthogonal zu E sind. Wir nennen
P 'elliptischen Pol' von E. Eine Ebenen-Quadrupel nennen wir e-normiert, wenn
f(e ; e) = 1 gilt. Die elliptische Größe der Winkels zwischen D und E ist für e-normierte Ebenen-Quadrupel
durch arccos( f(d ; e) ) gegeben.

P und Q mit den Quadrupeln und nennen wir zueinander 'polar', wenn
gleich Null ist. Jede Ebene durch P ist elliptisch orthogonal
zu jeder Ebene durch Q. Genau die zu P polaren Punkte liegen in der Ebene, zu der P der Pol ist. Wir nennen
das Punkt-Quadupel p 'e-normiert, wenn fp(p ; p) = 1 ist. Für e-normierte Quadrupel gibt arccos( fp(p ; q) )
den 'elliptischen signierten Abstand' an. Wir geben ihn wie die Winkel-Größe im Grad-Maß an. Gelegentlich
wird hierbei eine Winkel-Größe zwischen 90° und 180° durch ersetzt. Dann sprechen wir vom
'unsignierten' Abstand oder vom 'Betrag' des Abstands.

Eine Gerade g im projektiven Raum beschreiben wir durch ein Paar (u ; v) zweier Tripel aus reellen Zahlen,
die nicht beide nur aus Nullen bestehen.. Wenn g nicht ganz in der unendlich fernen Ebenen liegt, also affine
Punkte enthält, gibt u einen Richtungs-Vektor von g an. v ist dann das Tripel aus den ersten drei Zahlen eines
Quadrupels der Ebene durch g und dem Koordinaten-Ursprung (0 ; 0 ; 0 ; 1), also einem Normalen-Vektor v
dieser Ebene. Die euklidische Länge des Vektors v ist bei dieser Definition zunächst unbestimmt, weil das
Quadrupel nach Multiplikation mit einer reellen Zahl r ungleich Null die gleiche Ebene beschreibt. Man legt
so fest, dass das Tripel des Fußpunktes des Lots vom
Ursprung auf g ist. Wenn u einen Kraft-Vektor angibt, dann gehört v zu einem Drehmoment. (u ; v) wird auch
als Tripel-Paar in Plücker-Koordinaten bezeichnet. Wenn u und v nicht beide das Null-Tripel sind, beschreibt
(u ; v) genau dann eine Gerade, wenn ist. Die Gerade zum Tripel-Paar
nennen wir 'polar' zur Geraden g zu (u ; v) , weil der Pol jeder
Ebene durch g auf liegt.

Zur Beschreibung der Inzidenz von Geraden mit Punkten und Ebenen hat sich die Plücker-Matrix (nach
Julius Plücker (1801-1868))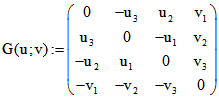
bewährt. Der Punkt liegt nämlich genau dann
auf der Geraden g zu (u ; v), wenn x.G(u ; v) das Quadrupel 0 mit vier Nullen ist. Dabei benutzen wir
den tiefgestellten Punkt für die Matrizen-Multiplikation und sehen x als Matrix mit einer Zeile an. Die
Ebene inzidiert mit g genau dann, wenn e.G(v ; u) = 0 ist. u und v sind also hier vertauscht.
Dann verläuft also g ganz in E.

Geraden h und g zu den Tripelpaaren (s ; t) und (u ; v) haben genau dann einen Punkt gemeinsam, wenn die
Bilinearform den Wert Null hat. Für jedes Geraden-Tripelpaar (u ; v) gilt
. Für metrische Untersuchungen benutzen wir außerdem die Bilinearform
. g und h sind nämlich genau dann elliptisch orthogonal, wenn nicht nur
gg((s ; t) ; (u ; v)) = 0 ist, sondern auch fg((s ; t) ; (u ; v)) = 0. Wegen k > 0 ist auch fg((u ; v) ; (u ; v)) für
jedes Geraden-Tripelpaar eine positive Zahl. Indem man eventuell alle Komponenten von (u ; v) durch die
Wurzel aus dieser Zahl teilt, erhält man ein Tripelpaar (u' ; v'), das die gleiche Gerade beschreibt und für das
fg((u' ; v') ; (u' ; v')) = 1 gilt. Wir nennen (u' ; v') eine 'e-normiertes' Tripelpaar.

Für schneidende Geraden g und h kann man die Bestimmung der Größe des eingeschlossenen Winkels auf
die Winkel-Messung zwischen Ebenen zurückführen, indem man die Ebenen betrachtet, die neben g bzw.
h auch die Gerade j enthält, die durch den Schnittpunkt von g und h geht und zu g und h elliptisch orthogonal
ist. Die so berechnete Winkel-Größe stimmt für e-normierte Geraden g und h zu den Tripel-Paaren (s ; t) und
(u ; v) mit dem Arccos-Wert von fg((s ; t) ; (u ; v)) überein.

Zur Beschreibung der metrischen Beziehungen variieren wir die Matrix G(u ; v) zu GS(u ; v), indem wir die
Zahlen in der vierten Spalte mit k multiplizieren. Die Matrix nennen wir zu GS(u ; v)
'polar'. Es gilt , wobei die Matrix
mit lauter Einsen in der Hauptdiagonalen ist und sonst nur Nullen. Außerdem ist
.

Eine elliptische Schraubung zur Achse g ist eine Bewegungen des elliptischen Raumes, welche
die Menge der Punkte von g und von festlässt. Sowohl die Inzidenz als auch die elliptische
Orthogonalität bleibt erhalten. Sei P ein Punkt mit dem Quadrupel und .
Wenn g durch ein e-normiertes Tripelpaar gegeben ist, gibt es zwei Zahlen und , so dass
p.M das Quadrupel des Bildpunktes von P ist. M bezeichnen wir auch durch .
Die Determinante von M ist 1. gibt die Größe des Winkel einer Drehung um g an und die
einer Drehung um die zu g polare Gerade. Wenn kein ganzzahliges Vielfaches von
ist, wohl aber , dann bleibt jeder Punkt auf g fest und jeder Punkt auf wird verschoben. Diese
Aussage bleibt wahr, wenn man die Winkel und die beiden Geraden vertauscht.

Wenn und ist, nennen wir die Schraubung 'Spiegelung an g'. Wenn h eine zu g
elliptisch orthogonale Gerade ist, gibt es zu eine zu g elliptisch orthogonale
Gerade j, so dass gilt: Die Hintereinanderschaltung der Spiegelungen an h und j stimmt mit
überein. Dabei ist j das Bild von h bei .

Schraubungen mit der gleichen Achse bilden eine abelsche Gruppe, und es ist
.

Sei P ein Punkt, der nicht auf g oder liegt. Dann ist
die Punktmenge eines einschaligen Hyperboloids. Dies soll im Folgenden illustriert werden.

In dieser Animation und auch den folgenden auf dieser Seite ist k gleich 1.

Jedes einschalige Hyperboloid trägt zwei Scharen von Geraden; die beiden werden auch 'Regulusse' oder
'Reguli' genannt. Durch jeden Punkt des Hyperboloids geht genau eine Gerade aus jedem der beiden
Regulusse. Zwei Geraden des gleichen Regulus schneiden sich nie, aber immer, wenn sie zu verschiedenen
Regulussen gehören. Die Geraden eines der beiden Regulusse nennen wir 'links-parallel', die des anderen
'rechts-parallel'.

Die Animation zeigt den Aufbau eines Netzes von Regulus-Geraden mit Hilfe von Schraubungen. Die roten
Geraden sind links-parallel, die blauen rechts-parallel. An sechzehn Punkte des magentafarbenen Kreises K
wird je eine rote und blaue Regulus-Gerade angeheftet. K entsteht durch Drehung des roten Punktes A(0;1;0)
um die x-Achse g. K ist also der Graf der Funktion .

Die beiden Regulus-Geraden, die an einen Punkt Q auf K angeheftet werden, ergeben sich folgendermaßen:
h sei die Gerade, welche den Koordinaten-Ursprung N(0;0;0) mit Q verbindet. Die rote bzw. blaue Regulus-
Gerade in Q ergibt sich durch eine Abbildung, die wir Rechts- bzw. Links-Translation längs h nennen. Zur
Unterscheidung von der euklidischen Translation wird sie nach William Clifford (1845-1879) auch 'Clifford-
Translation' genannt. Sie wird hier mit Hilfe einer realisiert, bei der bzw.
gesetzt wird. Dabei durchläüft die Werte von 0° bis 45°. Die rote bzw. blaue Regulus-Gerade durch Q
ist also das Bild von g bei der Abbildung bzw. . Der
Übergang von g zu diesen beiden Geraden wird in der Animation dadurch demonstriert, dass zwei Rechtecke,
die zunächst in der Ebene E von g und h liegen, um h gedreht werden, und zwar mit jeweils gleichem
Drehwinkel in entgegengesetzte Richtungen. Für sind die Rechtecke ausgeartet, da zwei der
gegenüberliegenden Seiten die Länge Null haben. Der in der Zeichnung angezeigte Drehwinkel stimmt mit
der Größe des Winkels zwischen E und jeder der beiden Rechteck-Ebenen Dl und Dr überein. Dieser
Winkel kann auf Grund der speziellen Lage von g als Gerade durch N euklidisch gemessen werden, also
mit Hilfe des Arccos-Wertes vom inneren Produkt aus den Tripeln der Normalen-Vektoren von E und Dl
bzw. Dr mit der Länge 1 . Bei einer anderen Lage von g muss der Winkel elliptisch gemessen werden, indem
man das innere Produkt durch f(d ; e) ersetzt; e und d sind dabei e-normierte Quadrupel zu E und Dl bzw. Dr .

Die Gerade g ist auf Grund dieser Konstruktion sowohl links-parallel zu jeder roten Regulus-Geraden,
als auch rechts-parallel zu jeder blauen Regulus-Geraden.

Die Zahl an schwarzen Doppel-Pfeil zeigt den elliptischen Abstand der Pfeil-Endpunkte an.
Sein Betrag stimmt mit dem des Winkels zwischen E und Dl bzw. Dr überein.

Die fünf letzten Bilder der Gleitschau zeigen nach den Standbildern der Animation das farbig gefüllte Netz der
Regulus-Geraden. Dadurch wird deutlicher, dass diese Geraden ein einschaliges Hyperboloid erzeugen. In dem
Netz sind vier Kreuzungs-Punkte A, B , C und D ausgezeichnet. Im drittletzten Bild ist für einige der Regulus-
Geraden angezeigt, in welchem Verhältnis sie die Strecken AB, BC, CD oder DA teilen, und zwar bei einer
euklidischen und einer elliptischen Messung von Strecken. Wenn zum Beispiel S der Schnittpunkt einer Geraden
j mit der Geraden AB ist, dann teilt S die Strecke AB im Verhältnis . Im Fall, dass S nicht zwischen A und
B liegt, wird dieser Quotient mit -1 multipliziert. Die mit Betragsstrichen angegebenen Werte bedeuten hier
euklidische oder elliptische Abstände. Im Fall der elliptischen Messung wird auf das Minus-Zeichen verzichtet.
Es zeigt sich, dass bei jeder blauen Regulus-Gerade das Produkt der Teilverhältnisse, mit dem die Strecken
AB und CD geteilt werden, eine Konstante tvk ist. Bei elliptischer Messung ist sie 1, bei euklidischer 1,1716.
Entsprechend ist auch bei jeder roten Regulus-Gerade das Produkt der Teilverhältnisse, mit dem die Strecken
BC und DA geteilt werden, eine Konstante, nämlich der Kehrwert von tvk. Siehe dazu auch die Seite
Regelflächen > ' Hyperboloid 2'.

Die euklidische Teilverhältnis-Konstante tvk = 1,1716 ermöglicht die Angabe einer
Gleichung, die genau für die Punkt-Quadrupel des Hyperboloids erfüllt ist, nämlich
.
Dabei bezeichnen die Größen mit dem Dach Quadrupel von A, B , C , D und einem
beliebigen Punkt X des Hyperboloids, bei denen die vierte Komponente zu 1 normiert
ist, indem das Quadrupel eventuell durch die vierte Komponente geteilt wird..
Siehe dazu die Seite Regelflächen > ' Ceva'.

Das vorletzte Bild der Gleitschau zeigt, dass alle Zellen des Hyperboloid-Netzes elliptische Quadrate
sind. Die Eckpunkte sind anders als in der euklidischen Geometrie nicht komplanar. Im letzten Bild
sind auf den Geraden AB und AD elliptische und euklidische Abstände von A angegeben.

Die Animation illustriert, dass die Bilder eines Punktes A bei jeder Schraubung mit der gleichen
Achse g auf dem einschaligen Hyperboloid liegen, das nach dem Verfahren der vorangehenden
Animation aus g durch Clifford-Verschiebungen entsteht. A ist hier der Punkt (0 ; 1 ; 0) zum
Quadrupel a = (0 ; 1 ; 0 ; 1) und g die x-Achse. Die magentafarbige Kurve ist für jeweils feste
Werte von und der Graf der Funktion .

Im ersten Abschnitt der Animation durchläuft die Werte von 0° bis 360° , bei konstantem
. Um den Verlauf der Schraubenkurve deutlicher zu machen, wird dann der Augenpunkt
bei konstantem Werte-Paar (720° ; 360°) zunächst um die z-Achse und dann um die y-Achse
gedreht, bis er auf g liegt. Anschließend wird bei konstantem bis 720° erhöht. Die
hellgrünen Punkte markieren dabei die Schnittpunkte der magentafarbenen Schraubenkurve mit
dem hellgrünen Kreis, in dem das Hyperboloid von der y-z-Ebene geschnitten wird. Für das
Werte-Paar (720° ; 720°) entartet die Schraubenkurve zu einer Regulus-Geraden durch A. Im
vierten Abschnitt wird bei konstantem bis 360° verkleinert, anschließend wird der
Augenpunkt zurückgedreht und dann bis 0° verkleinert. Im letzten Bild der Animation ist die
Schraubungskurve die Hyperbel, die sich als Schnitt des Hyperboloids mit der x-y-Ebene ergibt.

In dieser Animation werden die Zusammenhänge der vorhergehenden mit anderen Parametern
dargestellt. Die Schraubungs-Achse g, die bisher mit der x-Achse zusammenfiel, wurde in den Punkt
P (0,2 ; 0,4 ; 0,2) verschoben und dann um P parallel zur x-y-Ebene gedreht. Der um g gedrehte
Punkt A hat hier das Koordinaten-Tripel (0,2 ; 1,4 ; 0,2). Die magentafarbene Spur von A ist ein
Kegelschnitt K, dessen Ebene g in einem Punkt M ungleich P schneidet. Alle Punkte von K haben
von P den gleichen Abstand bei elliptischer Messung, nicht aber bei euklidischer. K ist in euklidischer
Hinsicht kein Kreis, wohl aber in elliptischer.

Auch hier werden die Regulus-Geraden des Hyperboloids in einem Punkt Q von K dadurch erzeugt, dass
g mit einer Rechts- und einer Links-Translation längs der Geraden h durch P und Q verschoben wird. Jede
Translationen hat den Funktions-Term mit bzw. . Die Drehwinkel, die
bei den beiden Translationen auftreten, sind elliptisch gleich, aber euklidisch verschieden. Die angezeigten
euklidischen Winkel-Größen werden mit den grau markierten Winkeln bestimmt, die elliptischen mit den rot
bzw. blau markierten Winkeln.

Die so konstruierten Regulus-Geraden erzeugen ein Hyperboloid, dessen Gleichung auch hier mit Hilfe der
Teilverhältnis-Konstanten tvk bestimmt werden kann. Wie im vorletzten Bild der Gleitschau im Anschluss
an die Standbilder der Animation illustriert wird, ist sie jetzt 1,06264 . Ein Punkt X mit dem Quadrupel
liegt genau dann auf dem Hyperboloid, wenn mit den Punkten A, B , C und D gilt: .

Das letzte Bild der Gleitschau zeigt, dass hier die Zellen des Netzes aus Regulus-Geraden
keine elliptischen Quadrate sind, wohl aber elliptische Rauten.

Schraubungen zu Tripel-Paaren, die nicht zu Geraden gehören

Ein Tripel-Paar (u ; v) mit Tripeln u und v, die nicht beide das Null-Tripel 0 aus drei Nullen sind, gehört
zu einer Geraden, wenn das innere Produkt gleich Null ist. Es gibt aber
Schraubungen auch zu jedem Tripel-Paar (u ; v) ungleich (0 ; 0) mit dem inneren Produkt ungleich Null.
Als geometrisches Objekt ordnen wir dann (u ; v) nicht die Menge der Punkte einer Geraden zu, sondern
die Menge der Geraden h mit Tripeln (s ; t), für die Null ist. Im Fall eines
Tripels (u ; v) mit innerem Produkt Null einer Geraden g bedeutet diese Bedingung, dass die Geraden h
genau die g schneidenden Geraden sind. Falls das innere Produkt nicht Null ist, nennen wir die zu (u ; v)
gehörige Menge der Geraden h ein 'Gewinde' g. Die oben angegebene Definition für
kann aber bei einem Gewinde nur dann zu einer Inzidenz und Orthogonalität erhaltenden Abbildung (also
einer 'Bewegung') führen, wenn gleich Null ist.

Wir Generalisieren darum die oben angegebene Definition der Matrix M im Fall
bei einem beliebigen Tripel-Paar (u ; v) ungleich (0 ; 0) mit Hilfe zweier reeller Zahlen c und d, für die
ist:

Für und gilt dann , falls fg((u;v);(u;v)) = 1 und
gg((u;v);(u;v)) = 0 ist. Die Anwendung der Matrix M' auf Punkt-Quadrupel ergibt für jedes positive k
und jedes Tripel-Paar (u ; v) ungleich (0 ; 0) eine Inzidenz und Orthogonalität erhaltenden Abbildung des
elliptischen Raums, die wir als 'generalisierte Schraubung' bezeichnen. Diese
Definition kann nicht nur für positive k angewendet werden kann, sondern auch im Fall des euklidischen
Raums mit k = 0 und des hyperbolischen Raums mit negativem k.

Der Nutzen dieser Definition zeigt sich noch in einem weiteren Aspekt, der eine einfache Beschreibung der
von induzierten Abbildung der Menge aller Geraden ermöglicht. Wir schreiben
dazu die Paare reeller Zahlen in der Form , addieren nach der Regel
und multiplizieren auf Grund der Festsetzung
nach der Regel .
Dann gilt das Assoziativ-Gesetz, das Kommutativ-Gersetz und das Distributiv-Gesetz. Mit dem zu x
'konjugierten' Element definiert man als
'Norm' ND(x) von x. Wenn ND(x) ungleich Null ist, hat x ein multiplikatives Inverses, denn .

Für k = -1 ergeben sich so die komplexen Zahlen und für k = 0 die dualen Zahlen, die auf der Seite
'euklidische Raumgeraden>Höhen im 6-Rechteck' erklärt werden. Für positive k werden die Zahlen
als ano(r)mal-komplexe Zahlen bezeichnet. Ein Tripel-Paar kann
analog als Tripel dieser 'hyperkomplexen' Zahlen in der Form

geschrieben werden. Wenn ein zweites Tripel ist,
definieren wir ein inneres Produkt durch
.
Man errechnet dann, dass gilt. Analog kann man das
Kreuz-Produkt der euklidischen Geometrie übertragen:





Wenn Punkte mit abgebildet werden, dann wird dadurch auch die Abbildung
von Geraden und Gewinden festgelegt. Diese Abbildung wird für ein Tripel s hyperkomplexer Zahlen zu
einer Geraden oder einem Gewinde durch folgende Vorschrift beschrieben, falls die Norm von
ungleich Null ist:
(*)
Bei dieser Abbildung bleiben die Relationen und erhalten, für Bilder s' und w' von s und w gilt also
und . Insbesondere ist , folglich werden Geraden-Tripel auf
Geraden-Tripel und Gewinde-Tripel auf Gewinde-Tripel abgebildet. Für c = 0 ist die Abbildung eine
Spiegelung.
(Siehe dazu und zum Folgenden den im Kopf dieser Seite genannten Text, Kapitel 14)

Die acht reellen Parameter von verbinden wir zu vier hyperkomplexen Zahlen,
nämlich zu und den drei Zahlen des Tripels . Die Kombination (c ; u) und nennen
wir 'Gerawinde-Quaternion'. Dafür definieren wir eine Addition durch und eine
Multiplikation durch . Das zu (c ; u) 'konjugierte Element ist
hier (c ; - u) und die 'Norm' NQ von (c ; u) ist die hyperkomplexe Zahl . Falls
ungleich Null ist, hat (c ; u) das multiplikative Inverse . Für diese Verknüpfungen gilt das
Assoziativ-Gesetz, das Distributiv-Gesetz und das Kommutativ-Gesetz für die Addition, aber nicht für die
Multiplikation.

Die oben angegebene Abbildung (*) nennen wir 'die zum Gerawinde-Quaternion gehörige Schraubung'.
Dann gilt der folgende (als Satz 52 des im Kopf dieser Seite genanten Textes bewiesene)
Satz: Wenn man die zum Gerawinde-Quaternion (a ; s) gehörige Schraubung mit der zu (c ; u) verkettet,
ergibt sich die Schraubung, die zu gehört.