Es lebe die Geometrie!

Der Fermat-Punkt im Tetraeder und seine Verwandten

Pierre de Fermat (1601-1665) stellte 1646 die Aufgabe, den Punkt im Dreieck zu finden, für den die Summe
der Abstände von den Eckpunkten minimal ist. Die Lösung wurde von Evangelista Torricelli (1608-1647)
gefunden, der erkannte, dass vom Fermat-Punkt aus gesehen alle Dreieck-Seiten unter dem gleichen Winkel
erscheinen. Darum liegt der Fermat-Punkt auf den drei Kreisen zum Umfangswinkel 120° über den Dreiecks-
Seiten.

Im Tetraeder ist der Fermat-Punkt analog definiert als Punkt mit minimaler Summe der Abstände von den vier
Eckpunkten. Lorenz Lindelöf (1827-1908) zeigte, dass vom Fermat-Punkt aus die Seiten-Flächen des Tetraeders
unter einem Raumwinkel von 180° erscheinen. Es gibt aber bisher kein konstruktives Verfahren zur Bestimmung,
wohl aber ein Iterations-Verfahren zur näherungsweisen Berechnung.

Auf dieser Seite wird das Näherungs-Verfahren mit Hilfe des Gradienten der Funktion f dargestellt, die jedem
Punkt P des dreidimentionalen Raums die Summe der Abstände d(P;A)+d(P;B)+d(P;C)+d(P;D) von den
Eckpunkten des Tetraeders ABCD zuordnet. In kartesischen Koordinaten ist dies die Funktion
mit
Die Gradienten-Funktion g von f ist die Funktion, die jedem Punkt P des Raums den Vektor zuordnet,
in dessen Richtung von P aus die Funktion f am stärksten ansteigt. Man berechnet sie mit den partiellen
Ableitungen von f nach den Koordinaten von x :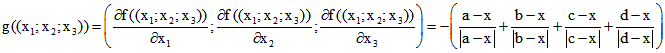
,
denn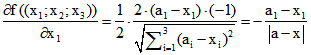
g(x) ist also der Gegen-Vektor des Vektors, der sich als Summe der Einheits-Vektoren von P nach den
Eck-Punkten von ABCD ergibt. In Richtung dieses Summe-Vektors nimmt f also ab. Bei dem Verfahren
des iterativen Gradienten-Abstiegs verschiebt man P ein kleines Stück gegen die Gradienten-Richtung,
berechnet dort den neuen Gradien und wiederholt das Verfahren mit immer kleineren Stücken.

Diese Animation zur Darstellung des iterativen Gradienten-Abstiegs zeigt das Tetraeder ABCD mit
großen farbigen Eck-Punkten und einen Test-Punkt X, der sich dem Fermat-Punkt von ABCD nähern
soll. Von X gehen vier Vektoren mit der Länge 1 aus, die in Richtung der Eck-Punkte von ABCD
zeigen. Die Pfeil-Spitzen bilden das Tetraeder , das wir Einheits-Tetraeder nennen. Es hat
eine Umkugel mit dem Radius 1. Das dritte Tetraeder mit violetten Kanten hat Seiten-Ebenen, welche
die Umkugel in den Eck-Punkten von berühren. Wir bezeichnen es mit ,
weil es ähnlich zu dem antipedalen Tetraeder zu X ist (siehe die Seite Fuß-Punkte), das hier nicht
eingezeichnet ist, dessen Kanten-Längen aber unten auf der Seite angegeben sind. Oben links sind die
Abstände X von A, B, C und D angegeben und die Größen der Raum-Winkel der Trieder mit der
Spitze X und den Basis-Dreiecken BCD , ACD , ABD und ABC . Der schwarze Pfeil ergibt sich
als Summe der Einheits-Vektoren.

Die Zeichnung unten rechts zeigt die entsprechende Konstruktion für ein Dreieck.

Das zweite Bild zeigt die Tetraeder nach der Verrückung in Richtung des Summen-Vektors um 0,05
seiner Länge. Die Zahl 0,05 nennen wir 'Schritt-Faktor. Nach insgesamt 88 Schrittenhat sich X so weit
dem Fermat-Punkt angenähert, dass die Raum-Winkel im Grad-Maß bei Rundung auf eine Nachkomma-
Stelle übereinstimmen. Dann hat sich das antipedale Tetraeder zu X so weit einem gleichseitigen Tetraeder
angenähert, dass die Kanten-Längen a, b, c und as, bs, cs bis auf drei Nachkomma-Stellen übereinstimmen.
Dann ist das antipedale Tetraeder nahezu ein gleichseitiges Tetraeder. In diesem schneiden sich sie die
gemeinsamen Orthogonalen der Gegegn-Kanten paarweise orthogonal im Schwerpunkt des Tetreders, der
zugleich das Umkugel-Zentrum ist (siehe die Seite Symmetrie).

Das antipedale Tetraeder zu X bezüglich ABCD wird anschließend hinzugezeichnet. Es
entsteht aus durch die Streckung, deren Zentrum und Faktor oben links angezeigt wird.
Die Konstruktion wird um 360° gedreht.

Diese Animation wiederholt die vorangehende Animation mit einem bemerkenswerten Unterschied:
Der rote Einheits-Vektor zeigt nämlich in die entgegengesetzte Richtung. Daraus ergibt sich ein
anderer Pfad des Test-Punktes X, der aber dennoch zu einem Punkt führt, der dem Fermat-Punkt
ähnelt. Nach 107 Schritten unterscheiden sich die Kantenlängen des antipedalen Tetraeders zu X
bis in drei Nachkomma-Stellen nicht von einem gleichseitigen Tetraeder und die Raumwinkel bei X
haben nahezu die Größe 180°. Dabei ist aber zu bedenken, dass der Grenz-Punkt X hier nicht
mehr im Innern von ABCD liegt und sich darum innere Punkte von ABCD nur die Trieder zur
BCD gibt. Die Summe der Abstände X von A, B, C, D ist größer als beim Fermat-Punkt.

Der entsprechende Vorgang beim Dreieck unten rechts ergibt einen Punkt, der analoge Gemeinsmkeiten
mit dem Fermat-Punkt hat

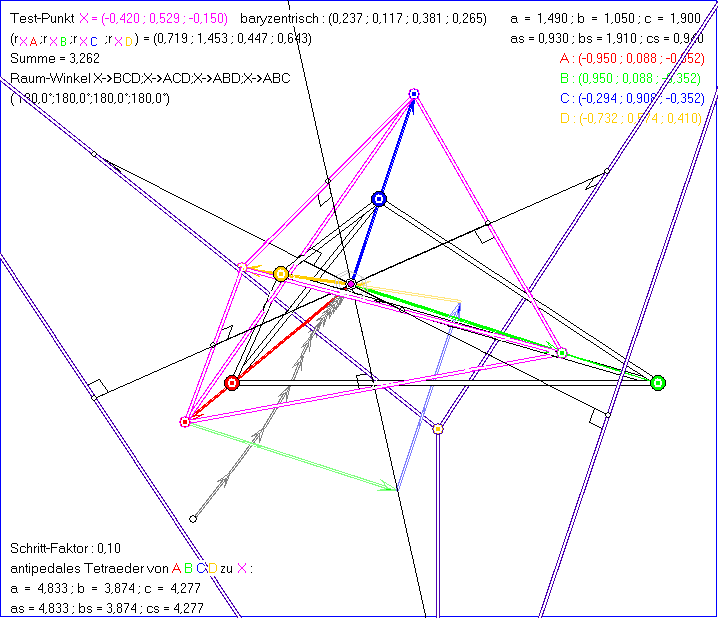
Die Gleitschau zeigt ein anderes Tetraeder ABCD als die vorhergehenden. Im ersten Bild wird der
Fermat-Punkt angenähert. Im zweiten Bild wurde der rote Vektor umgedreht, im dritten, vierten
und fünften der grüne, blaue bzw. gelbe, im sechsten der grüne und der gelbe und im siebenten
der rote und der grüne. Die Abstands-Summe X von A, B, C, D ist für den Fermat-Punkt im ersten
Bild kleiner als in den folgenden, vermutlich liegt bei allen diesen Grenz-Punkten ein relatives Minimum
der Abstand-Summe vor. Dafür gibt es aber bisher keinen Beweis.