Es lebe die Geometrie!

Kachelungen im Kreis-Modell, die mit Nachbar-Bewegungen aus einem
Dreieck mit einer der Signaturen 1-23, -12-3, 321 oder 3-21 erzeugt werden

In dieser Gleitschau sind positv orientierte Kacheln blau gezeichnet und negativ orientierte violett. Die
Kachelränder sind schwarz gezeichnet, wo gleichfarbige Kacheln zusammenstoßen, und sonst grün. Die
grüne Seite hat die Nummer 2 bei positiv orientierten Kacheln und bei negativ orientierten die Nummer
-2. Die Signatur 1-23 dieser Kachelung bedeutet, dass die hyperbolischen Nachbar-Bewegungen eines
positiv orientierten Kachel-Dreiecks K die hyperbolischen 180°-Drehungen um die Mitten der Seiten 1
und 3 bzw. -1 und -3 sind und außerdem die Spiegelung an der Seite 2 bzw. -2 sind. Für den Eckpunkt
Nummer 3 (der für die Basis-Kachel im Einheitskreis-Mittelpunkt N liegt) gilt folgendes Ecken-Schema:

Für eine Periode dieses Schemas ergibt sich also eine Winkelsumme von . Damit es
um N herum zu keinen Überlappungen kommt, muss ein ganzzahliges Vielfaches dieser Summe 360° sei,
folglich gilt mit einer ganzen Zahl n, die größer als 1 ist, weil in der hyperbolischen
Ebene die Summe der Innenwinkel im Dreieck stets kleiner als 180° ist.Die anderen Eckpunkte ergeben
die gleiche Bedingung. Darum ist sie auch hinreichend dafür, dass die Basis-Kachel eine Kachelung erzeugt.
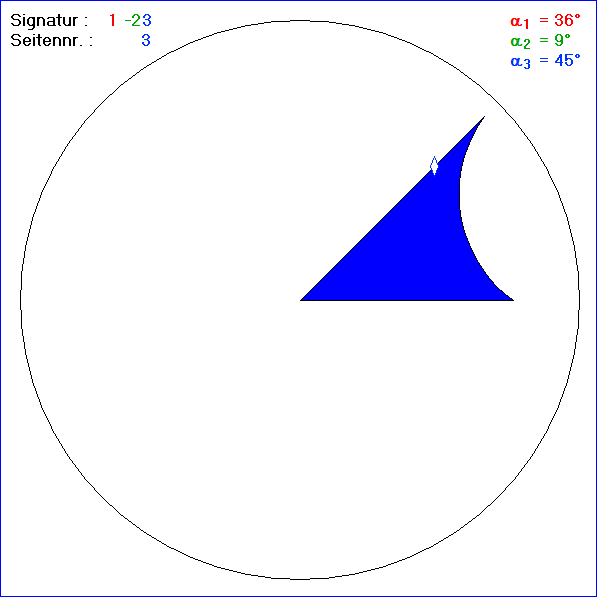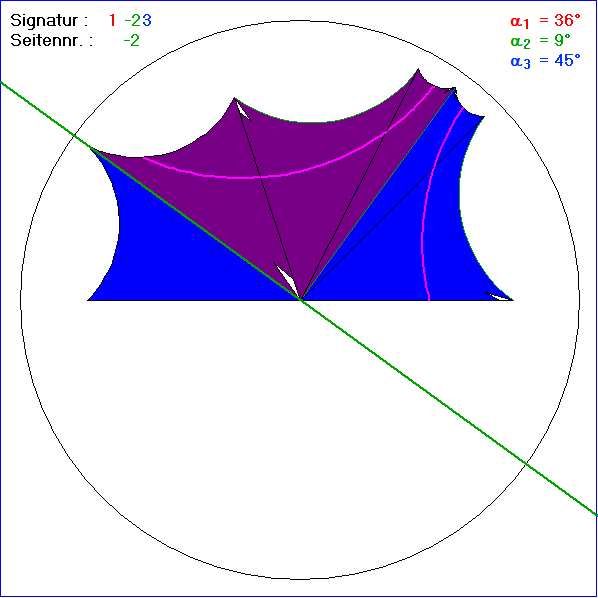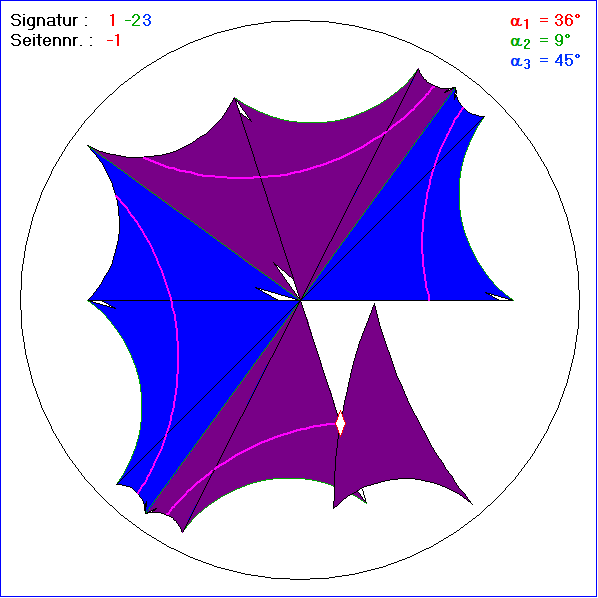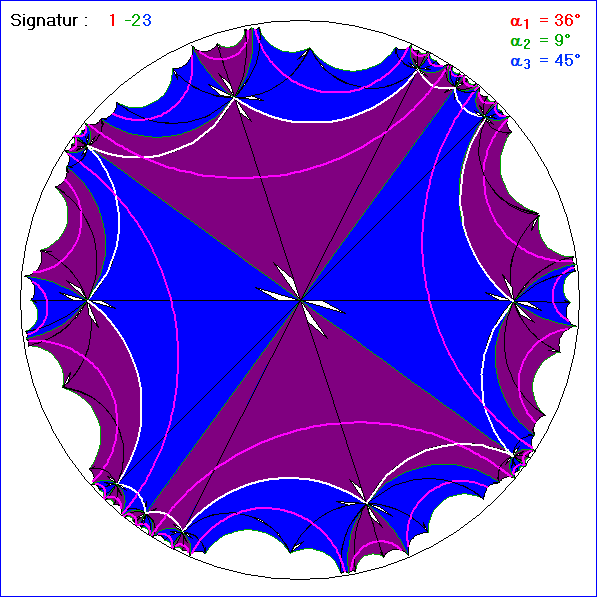
Bei den Kachelungen der Gleitschau ist n = 2. Darum sind alle Innenwinkel der grün berandeten blauen bzw.
violetten Flächen rechtwinklig, denn dort treffen drei gleichfarbige Kacheln mit paarweise verschiedenen
Ecken-Nummern zusammen. Die magentaroten Kreisbögen setzen sich aus den Verbindungen der Mitten
von den Seiten mit dem Nummer-Betrag 1 und 3 zusammen, so dass in der vollständigen Kachelung ganze
hyperbolische 'Geraden' entstehen, also Kreisbögen, die vom Einheitskreis aus dazu orthogonalen Kreisen
ausgeschnitten werden. Auch die grünen Seiten mit dem Nummer-Betrag 2 fügen sich zu vollständigen
'Geraden' zusammen. Diese schneiden sich zu Teil, und zwar dann stets orthogonal, während sich die
magentaroten 'Geraden' nie treffen. Man kann die Zusammenfassung gleichfarbiger Kacheln, die längs einer
magentaroten 'Geraden' aufgereiht sind, als neue Kacheln betrachten. Diese haben unendlich viele Seiten
mit gleicher hyperbolischen Länge, an jeder Ecke einen rechten Winkel und sie gehen durch Spiegelungen
an ihren Seiten auseinander hervor. Die Schnittpunkte der magentaroten 'Geraden' mit den schwarzen
Seiten sind Symmetriepunkte dieser Kacheln. Ein Vergleich mit der Kachelung mit der Signatur 1-23 in der
euklidischen Ebene zeigt, dass die neuen Kacheln dort Streifen von aneinandergesetzten Dreiecken mit
parallelen Rändern entsprechen, die ins Unendliche reichen. Die magentaroten 'Geraden' entsprechen dort
den Mittellinien der Streifen und sind für alle Streifen parallel.

Das Bild 2 der Gleitschau entsteht aus dem Bild 1 wenn man das Basis-Dreieck hyperbolisch verschiebt.
Bild 3 zeigt eine Kachelung mit gleicher Signatur für ein gleichseitiges Dreieck.

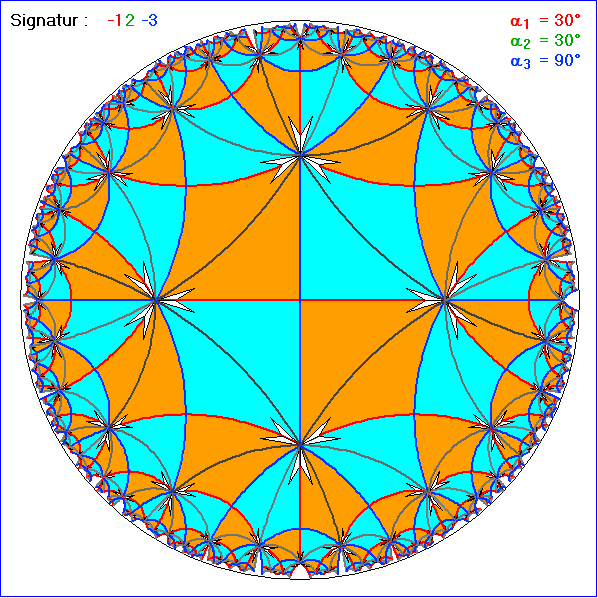
Zu der Signatur -12-3 gehören folgende Ketten-Schemata:


Daraus folgt, dass ein ganzzahliges Vielfaches von bzw. gleich 360° sein muss. Es
folgt und mit natürlichen Zahlen m und n größer als 1, die nicht beide gleich
2 sind. Unter diesen Bedingungen erzeugt eine Dreieck durch Spiegelungen an den Seiten 1 und 3 bzw. -1
und -3 und 180°-Drehungen um den hyperbolischen Mittelpunkt von Seite 2 bzw. -2 stets eine Kachelung.

In der Gleitschau wurden benachbarte Dreiecke, die an der Seite 2 oder -2 zusammentreffen in der gleichen
Farbe gezeichnet, und zwar hellblau für positiv orientierte Dreiecke und sonst orangefarben. Auf diese Weise
ergibt sich eine neue Kachelung aus punktsymmetrischen Vierecken, die in der euklidischen Ebene den
Parallelogrammen entsprechen. Benachbarte Vierecke gehen dabei durch Spiegelung an der gemeinsamen
Seite auseinander hervor. Die Seitenbögen schließen sich zu vollen hyperbolischen 'Geraden' zusammen.
Dies gilt bemerkenswerter Weise auch für die schwarz gezeichneten Diagonalen. Die teilweise magentarot
eingezeichneten Mittellinien ergeben jedoch keine 'Geraden' . Die Spiegelungen an den Viereck-Seiten sind
Automorhismen der Kachelung der Vierecke, d. h. das Spiegel-Bild jeder Kachel gehört zur Kachelung.
Dies gilt aber nicht für die schwarzen Diagonalen.

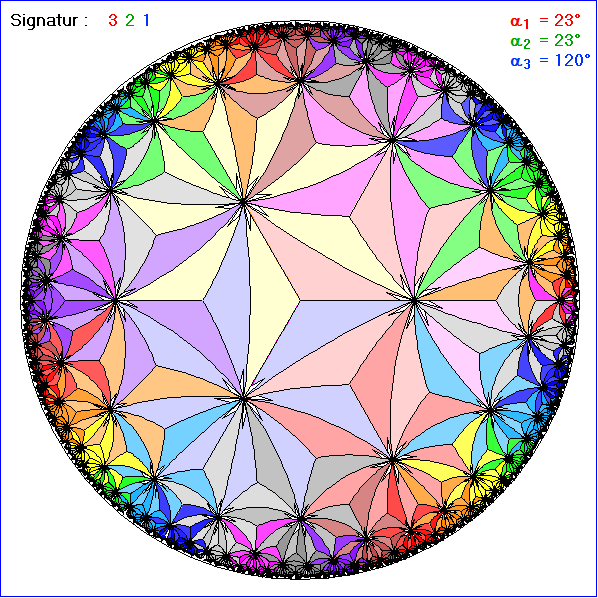
Die Gleitschau zeigt Kachelungen zur Signatur 321. Darum ist die Nachbar-Bewegung B1 eine
gerade hyperbolische Bewegung, welche die Seite 3 auf die Seite 1 abbildet, d. h. sie ist eine
hyperbolische Drehung um die Spitze der Seite 3, also den Eckpunkt Nummer 3. Die Bewegung
B2 ist die Drehung um den hyperbolischen Mittelpunkt der Seite 2 und die Bewegung B3 die
Umkehr-Abbildung von B1. Die Seiten Nummer 1 und 3 sind also gleich lang und die Innenwinkel
bei den Spitzen der Seiten 1 und 2 gleich groß. Die Ketten-Schemata zu den Eckpunkten Nummer
3 und 2 sind:


Eine notwendige und hinreichende Bedingung dafür, dass ein Basis-Dreieck eine Kachelung
erzeugt ist darum, dass es natürliche Zahlen m und n gibt mit und .
Dabei ist wie bei jedem Dreieck die Bedingung Bedingung für die Existenz
des Basis-Dreiecks. Daraus folgt die Ungleichung .

Im ersten Bild der Gleitschau wurden in der Kachelung zu einem Basis-Dreieck mit m = 3 und
n =7 alle Kacheln, bei denen die Spitzen ihrer Seite 1 zusammenfallen in gleicher Farbe gezeichnet,
so dass eine neue Kachel in Form einer Blüte entsteht. Bei Bild 2 fallen die Spitzen der Seite 2
zusammen und beim Bild 3 die der Seite 3. Bild 2 unterscheidet sich wenig von Bild 1, da die
Eckpunkte mit den Nummern 2 und 3 an den gleichen Stellen liegen. In Bild 3 sind die neuen
Kacheln dagegen gleichseitige Dreiecke. Entsprechende Zusammenhänge werden in der Gleitschau
auch für andere Werte von n und m dargestellt.

Aus der Tatsache, dass jedes der Basis-Dreiecke zur Signatur 321 eine Kachelung erzeugt, folgt
durch Zusammenfassung der Kacheln mit gleichem Eckpunkt Nummer 3, dass auch jedes regelmäßige
m-Eck eine Kachelung erzeugt, vorausgesetzt, dass darin jeder Innenwinkel die Größe hat
und gilt. Die Nachbarbewegungen sind dabei die 180°-Drehungen um die Seitenmitten.

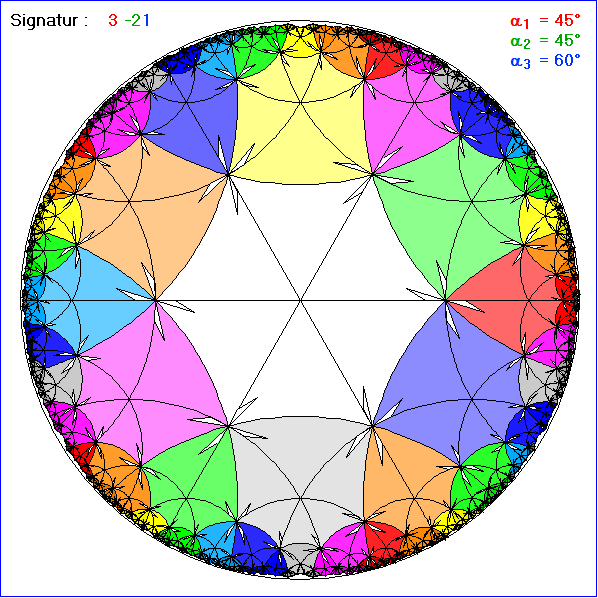
Die Signatur dieser Kachelungen ist 3-21. Die Bewegungen B1 und B3 sind also zueiander inverse
Drehungen um den Eckpunkt 3, und die Bewegung 2 ist eine Spiegelung an der Seite 2. Folgende
Ketten-Schemata treten auf:


Darum sind die Ecken-Bedingungen und mit natürlichen Zahlen m und n,
für die gilt.

Die Gleitschau zeigt verschiedene Zusammenfassungen der Dreiecke, so dass Kachelungen mit
regelmäßigen m-Ecken oder rautenförmige Vierecken entstehen.