Es lebe die Geometrie!

Steiner-Zykloide (auch Deltoid genannt)
(hier auch als -3-Zykloide bezeichnet)

Die Steiner-Zykloide entsteht als Spur eines Punktes am Rand eines 'Gangkreises', der innen an
einem 'Rastkreis' abrollt. Dabei beträgt der Radius des Gangkreises 1/3 tel oder 2/3 tel vom
Radius des Rastkreises. Wenn der größere Gangkreis gewählt wird, ist liegt der Durchmesser
durch den die Spur zeichnenden Punkt stets auf einer Tangente der Steiner-Zykloide.

A sei die Mitte eines Bogens der Steiner-Zykloide Z. Die Evolvente von Z durch A ist eine dazu
ähnliche Zykloide mit einem 1/3 tel so großen Rastkreise. Die Ortskurve der Krümmungsmittelpunkte
dieser Evolvente (also ihre Evolute) ist die Ausgangs-Zykloide Z. Der Begriff 'Evolvente' oder
'Abwickelkurve' entsteht aus folgender Vorstellung: Man betrachte eine Ausstech-Form für Kuchen-
Plätzchen in Form einer Steiner-Zykloide. Man befestigt in ihrem Innern in einem Spitzen-Punkt einen
Faden, spannt ihn über einen Bogen von Z bis zur Bogenmitte und schneidet ihn dort ab. Wenn man
dann das Fadenende in gestraffter Form hin- und herbewegt, beschreibt dieses Ende einen Bogen der
Evolvente. Alternativ stellt man sich eine Gerade vor, die anfangs die Steiner-Zykloide im A berührt
und dann ohne zu rutschen daran abrollt. Die Spur des Punktes der Gerade, der anfangs auf A fiel,
ist dann die Evolvente.durch A. Wenn A ein anderer Anfangspunkt ist, ergibt sich eine andere Kurve,
die ebenfalls 'Evolvente' genannt wird. Wenn im Folgenden der Begriff 'Evolvente' ohne Nennung eines
Anfangspunktes verwandt wird, ist stets die Evolvente durch eine Bogenmitte gemeint

Der Gangkreis hat im Folgenden stets den Radius 1.

Spur vom 2/3-Gangkreis
Der Gangkreis mit dem Radius 2/3
rollt ohne zu Rutschen am Rastkreis ab.

Spur beider Gangkreise
Die Gangkreise mit den Radien 1/3
und 2/3 rollen in entgegengesetzter
Richtung mit der gleichen Spur ab.
Der Spurpunkt ist kollinear mit den
Rastkreis-Berührpunkten.

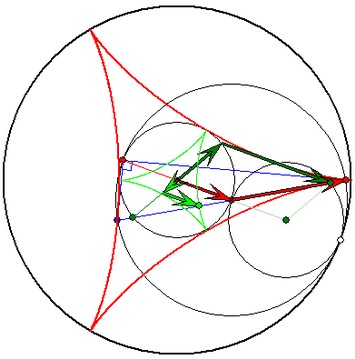
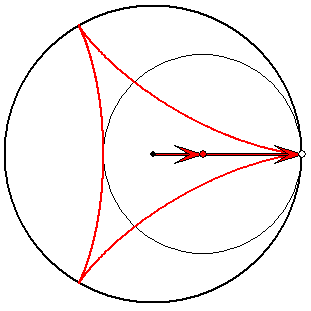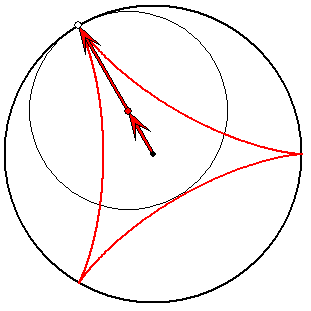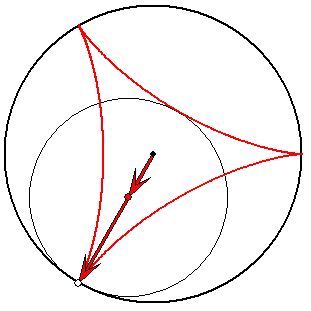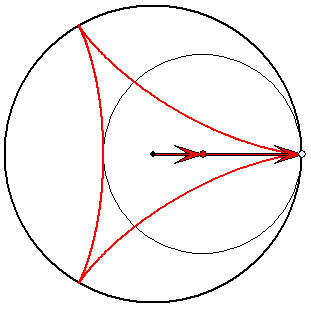
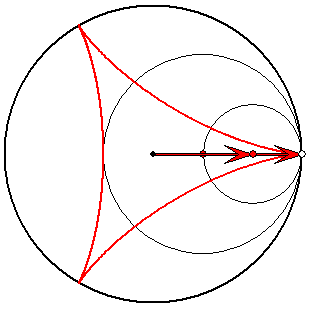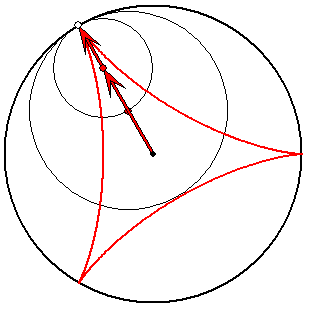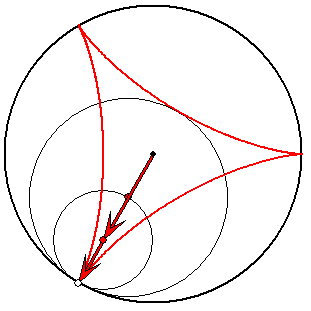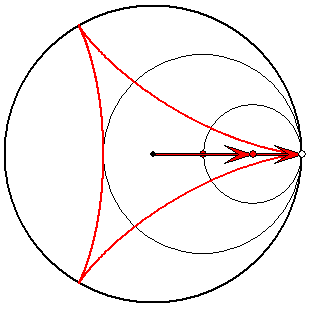
Steiner-Zykloide (rot) mit Evolvente (hellgrün)
Die roten und die dunkelgrünen Pfeile haben die Länge
1/3 und 2/3. Die hellgrünen Pfeile haben ein Drittel der
Längen der entsprechenden dunkelgrünen. Zum
Verständnis der Roll-Eigenschaft des Kreises zu den
dunkelgrünen Pfeilen ist es nützlich, sich die
Reihenfolge der Pfeile vertauscht vorzustellen.

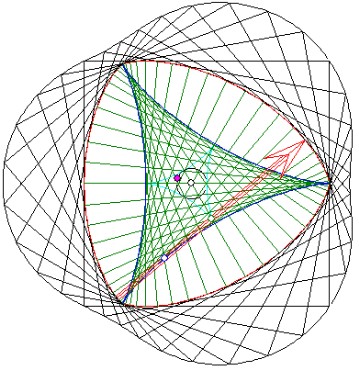
Steiner-Gleichdick mit Quadraten
Die dem Steiner-Gleichdick umbeschreibenen
Quadrate mit den Seitenlängen 16/9 haben ihre
Mittelpunkte alle auf einem Kreis mit dem Radius
1/9. Der rote Punkt ist der Mittelpunkt eines
Quadrates, von dem zwei Seiten parallel zu dem
roten Pfeil sind, der gegenüberliegende
Berührpunkte verbindet.

Minkowski-Addition vom Gleichdick
und seinem Spiegelbild
Unter der Minkowski-Addition zweier Vektormengen
A und B versteht man die Menge der Vektoren a+b,
wobei a bzw. b ein Vektor in A bzw. B ist. Als Menge
A wurde hier die Menge der Ortsvektoren von Punkten
innerhalb der Randkurve des Steiner-Gleichdicks
gewählt und als B die Menge die daraus durch
Punktspiegelung am Ursprung entsteht. A+B ist dann
die Vektormenge eines Kreises. Der Umfang des
Gleichdicks ist halb so lang wie der des Kreises, da

gilt, wenn A und B zu konvexen Mengen gehören.

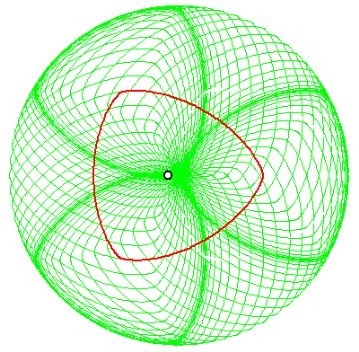
Zusammenhang zwischen der Steiner-Zykloide und der zugehörigen Epizykloide
Diese Animation zeigt den Zusammenhang zwischen der -3-Zykloide, die dadurch entsteht, dass
ein Gangkreis vom Radius 1/3 im Innern des Rastkreise abrollt (Hypozykloide), mit der +3-Zykloide,
bei der ein Gangkreis gleicher Größe außen abrollt (Epizykloide). Die Verbindungsgerade der die Spur
zeichnenden roten Punkte P und Q auf den Gangkreisen ist Tangente der Steiner-Zykloide. Sie ist
orthogonal zu der blauen Geraden, welche die Rastkreis-Berührpunkte der Gangkreise vom Radius
2/3 und 4/3 verbindet. Der Punkt, der die Strecke PQ im Verhältnis 2 : 1 = (3+1) : (3-1) teilt, liegt auf
dem Steiner-Gleichdick. Die roten Pfeile mit den Längen 1/3 und 2/3 gehören zu der Steiner-Zykloide.
Die entsprechenden Pfeile für die +3-Zykloide wurden nicht gezeichnet. Ihre Längen sind 1/3 und 4/3.