Es lebe die Geometrie!

Muster mit nur einer Seitenlänge,
die aus durch Nachbarbewegungen erzeugten Kachelungen abgeleitet werden

In den archimedischen Kachelungen der vorhergehenden Seite kommt nur eine Seitenlänge vor. Außerdem
sind dort in jeder Kachel die Innenwinkel gleich groß. Diese Einschränkung wird auf dieser Seite fallengelassen.

Die Animation zeigt den Aufbau einer Kachelung zur Signatur -1-2-3 für ein Ausgangsdreieck ABC
mit den Innenwinkeln 90°, 60° und 30°. Dabei wird gleichzeitig das Muster erzeugt, das sich ergibt,
wenn man die Nachbarbewegungen auf den gelben B-Ankreismittelpunkt anwendet. Dieses Muster
besteht aus zum Teil überschlagenden regulären Polygonen mit den gleichen Seitenlängen. Wegen der
Überlappungen bildet das Muster keine Kachelung. Die Gleitschau zeigt im Anschluss an die Animation
Standbilder daraus.

In der Animation werden die abgeleiteten Muster zur Ausgangskachelung mit der Signatur -1-2-3 und dem
90°-60°-30°-Dreieck ABC dargestellt, die sich ergeben, wenn man für den erzeugenden gelben Punkt P
nacheinander folgende Punkte wählt:
1. Inkreis-Zentrum I von ABC
2. A-Ankreis-Zentrum von ABC
3. B-Ankreis-Zentrum von ABC
4. C-Ankreis-Zentrum Z von ABC
5. Schnittpunkt von BI mit AC
6. Schnittpunkt von CI mit AB
7. Schnittpunkt von AZ mit BC
8. Schnittpunkt von BZ mit AC
Dabei wird jedes Polygon des abgeleiteten Musters aus dem Punkt gestreckt, der gemeinsamer Eckpunkt
der Kacheln in der Ausgangskachelung ist, zu denen die gelben Eckpunkte des Polygons gehören.

Die Animation zeigt abgeleitete Muster zu der Ausgangskachelung mit der Signatur 213 und dem
Start-Dreieck ABC mit den Innenwinkel 120°, 30° und 30°. Die Nachbar-Bewegungen B1 und B2
sind Drehungen um A mit den Drehwinkeln 120° bzw. -120°. B3 ist die Spiegelung am Mittelpunkt M
der Strecke BC. Der gelbe Punkt P zur Erzeugung des abgeleiteten Musters bewegt sich auf dem Kreis,
die Seiten AB und AC in B bzw. C berührt. Dies ist der C-Apollonius-Kreis im Dreieck AMC, das
bei A und M die Hälfte der Drehwinkel von B1 bzw. B3 als Innenwinkel hat. Er ist also die Äquidistanzkurve
der Drehungen B1 und B3. Solange P sich innerhalb von ABC befindet, ergibt das Muster eine Kachelung
mit gleichseitigen Dreiecken und regelmäßigen 6-Sternen.

Die Gleitschau zeigt im Anschluss an die Animation zeigt Vergrößerungen und Standbilder daraus. Die
6-Sterne werden auch dann in gleicher grüner Farbe gezeichnet, wenn sie gemeinsame Seiten haben,
weil sie durch eine Nachbar-Bewegung auseinander hervorgehen.

Hier wurde ein gleichschenkliges Dreieck ABC mit rechtem Winkel bei B als Ausgangskachel gewählt mit der
Signatur -132. Die Nachbarbewegung B1 ist also die Spiegelung an AC und B2 bzw. B3 die Drehung um 90°
bzw. -90° um B. Um ein abgeleitetes Muster mit nur einer Seitenlänge zu erzeugen, muss der gelbe Punkt P
auf der Äquidistanzkurve von B1 und B2 liegen. Dies ist der geometrische Ort der Punkte Q mit folgender
Eigenschaft: Sei d der Abstand von der Geraden AC und r der Abstand von dem Punkt B. Dann ist
. Da hier d kleiner als r ist, muss die Äquidistanzkurve eine Hyperbel mit AC als Leitgerade
und B als Brennpunkt sein.

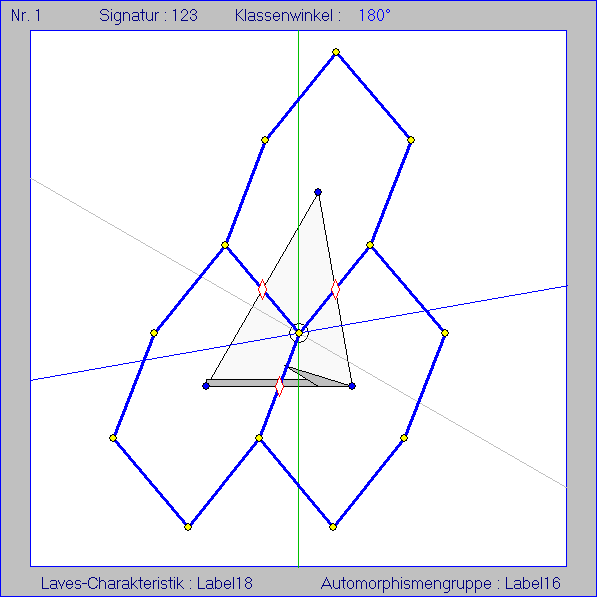
Die Gleitschau zeigt für die 46 Typen von durch Nachbarbewegungen erzeugten Kachelungen der Seite
' 46 Typen periodischer Kachelungen' die Äquidistanzkurven aller Paare von Nachbarbewegungen. Dazu
wird jeweils ein gelber Punkt P zur Bestimmung eines abgeleiteten Musters angegeben. Wenn es einen
gemeinsamen Punkt der Äquidistanzkurven gibt, wird er als Ort von P gewählt, so dass in dem abgeleiteten
Muster nur eine Seitenlänge vorkommt. Wenn es keinen gemeinsamen Punkt gibt, wurde P so gesetzt,
dass die Summe der Quadrate von den Differenzen zwischen den Abständen des Punktes P von jeweils
zwei seiner Nachbarbewegungsbildern möglichst klein war. Einige der Signaturen sind dadurch
ausgezeichnet, dass es stets Punkte P gibt, für die das abgeleitete Muster nur eine Seitenlänge enthält.
Die Signaturen, für die dies nicht gilt, sind in der Gleitschau daran erkennbar, dass die Ausgangskachel
in dunklerem Grau gezeichnet ist. In dem Fall wurden zu der Signatur zwei Beispiele angegeben, von
denen ein Beispiel Äquidistanzkurven mit einem gemeinsamen Punkt zeigt.

Die Art der Nachbarbewegung ist bei Drehungen an Hand des kleinen roten Polgons um den Drehpunkt und
bei Achsen- oder Gleitspiegelungen an Hand der durchgezogenen bzw. gestrichelten roten Achse erkennbar.

Die Äquidistanzkurve zu Nachbarbewegungen B1 und B2 hat folgende Eigenschaften:

1. Fall: B1 und B2 sind Drehungen. Bei gleichem Drehpunkt gibt es keine Äquidistanzkurve. Denn
wenn die Beträge der Drehwinkel gleich sind, stimmen die Abstände für alle P der Ebene überein, und
andernfalls nur für den Drehpunkt. Bei verschiedenen Drehpunkten A und B ist die Mittelsenkrechte
von AB Äquidistanzkurve, wenn die Beträge der Drehwinkel gleich sind. Andernfalls ist die
Äquidistanzkurve der C-Apolloniuskreis in dem Dreieck ABC, wobei der Winkel CBA bzw. BAC
die Hälfte des Drehwinkels von B2 bzw. B1 ist.

2. Fall: B1 und B2 sind Translationen. Dann gibt es keine Äquidistanzkurve. Denn im Fall gleicher
Verschiebungslängen sind die Abstände für alle P der Ebene gleich, und andernfalls für keinen Punkt.

3. Fall: B1 ist Drehung und B2 Translation mit der Verschiebungslänge v. Dies kommt nur beim
Drehwinkel 180° vor. Die Äquidistanzkurve ist dann der Kreis um den Drehpunkt mit der Hälfte
von v als Radius.

4. Fall : B1 und B2 sind Gleitspiegelungen oder Achsenspiegelungen. Jede Gleitspiegelung ist die
Hintereinanderschaltung der Spiegelung an ihrer Achse und einer Verschiebung längs der Achse.
Bei der Achsenspiegelung ist diese Verschiebung die identische Abbildung. Die Verschiebungslängen
von B1 und B2 seien u bzw. v mit . Bei Achsenspiegelungen ist ihr Wert also Null. Wenn g bzw.
h der Abstand des Punktes P von der Achse von B1 bzw. B2 ist, dann ist der Abstand des
Gleitspiegelungsbildes von P gleich bzw. . Gleichheit besteht genau
dann, wenn . Sei . Im Fall c = 0 ist
die Äquidistanzkurve das Winkelhalbierenden-Paar der Achsen. Sei nun . Dies kommt bei den
46 Typen von Kachelungen, die durch Nachbarbewegungen erzeugt werden, nur vor, wenn B1 und B2
Gleitspiegelungen mit orthogonalen Achsen sind oder die Achsen parallel verlaufen. Bei orthogonalen
Achsen ist die Äquidistanzkurve eine Hyperbel mit gleichen Halbachsen-Längen und den
Winkelhalbierenden der Achsen als Asymptoten. Es seien nun zueinander parallele Achsen betrachtet
mit dem Abstand d, und zwar zunächst der Fall, dass der Punkt P der Äquidistanzkurve zwischen den
Achsen liegt. Dann ist g + h = d und folglich und . Wegen
ist dies nur bei möglich. Wenn P nicht zwischen den Achsen liegt, ist , folglich
und ebenfalls , wobei dies wegen nur bei
vorkommen kann.

5. Fall : B1 ist Gleitspiegelung oder Achsenspiegelung mit der Verschiebungslänge u und B2 Drehung mit
dem Drehwinkel . P habe von der Achse den Abstand g und vom Drehpunkt den Abstand r. Die
Abstände des Punktes P von seinen beiden Bildern sind dann gleich, wenn .
Wir führen ein kartesiches Koordinatensystem ein mit der Achse als y-Achse und dem Drehpunkt beim
Punkt (d ; 0). Für den Punkt P(x;y) gilt dann

Für ist dies äquivalent mit , wobei .
Dies ist die Gleichung einer Parabel mit dem Scheitelpunkt bei (m ; 0) und dem Halbparameter d.
kommt nur vor, wenn u = 0 ist. Dann ist das Verhältnis des Abstands des Punktes P von der Achse
und vom Drehpunkt die Konstante und folglich die Äquidistanzkurve die Hyperbel mit dem
Drehpunkt als Brennpunkt und der Achse als Leitgerade.

6. Fall : B1 ist Gleitspiegelung oder Achsenspiegelung mit der Verschiebungslänge u und B2 eine Translation
mit der Verschiebungslänge v. Die Äquidistanzkurve ist dann das Paar der Geraden die von der Achse den
Abstand , falls v größer als u ist; andernfalls gibt es keine Äquidistanzkurve.