Es lebe die Geometrie!

Die Strecke als Zykloide

Der Rastkreis hat auch hier stets den Radius 1.

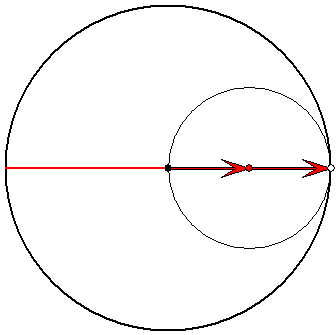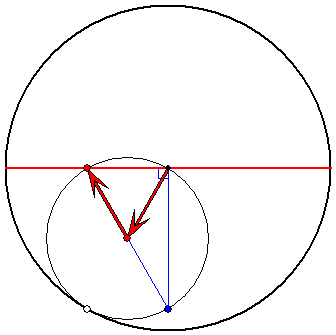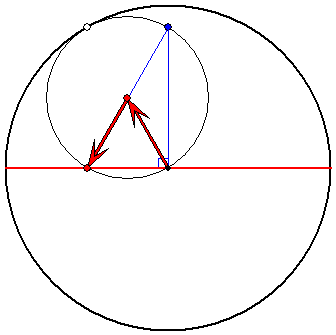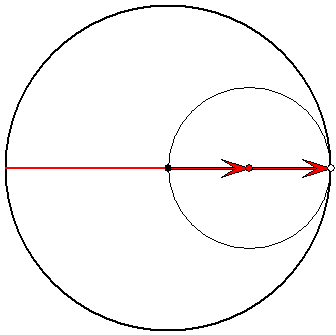
Die Strecke als Zykloide
Der Gangkreis hat hier den Radius 1/2. Die
zugehörigen Pfeile habe beide die gleiche
Länge. Sie drehen sich mit gleicher
Geschwindigkeit gegenläufig. Der Gegenpunkt
des Spurpunktes auf dem Gangkreis bewegt
sich auf einer zur Strecke orthogonalen Geraden.

Hüllkurve des Gangkreis-Durchmessers
Die Geraden durch den Spurpunkt und das Zentrum
des Gangkreises sind alle Tangenten einer Kurve, die
als Hüllkurve (Envellope) dieser Geraden bezeichnet
wird. Sie ist eine Astroide (-4-Zykloide), die von einem
Gangkreis mit dem Radius 1/4 erzeugt wird.

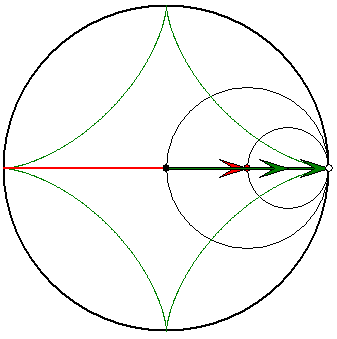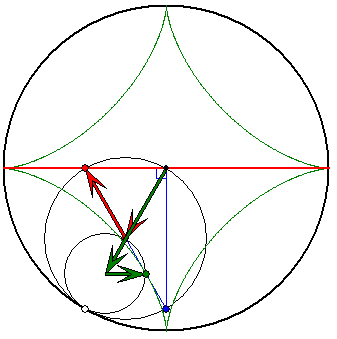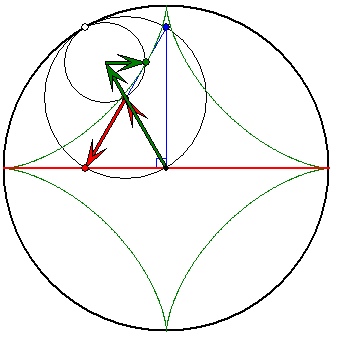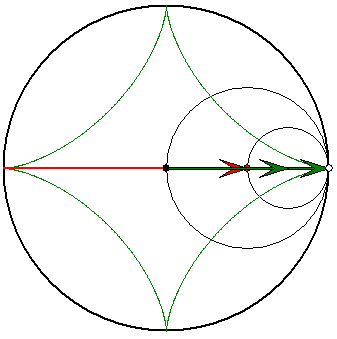
Evolvente und Triphil
Die Animation zeigt für die -2-Zykloide die Konstruktion einer Figur, die dem Steiner-Gleichdick bei der
-3-Zykloide entspricht. Während das Steiner-Gleichdick in einem Quadrat so gedreht werden kann, dass
stets alle vier Seiten berührt werden, hat diese Figur die Eigenschaft, dass sie sich in einem gleichseitigen
Dreieck so drehen lässt, dass alle drei Seiten Tangenten sind. Wir nennen die Figur darum ein 'Triphil'. Wie
bei der Konstruktion des Steiner-Gleichdicks wird auch hier die hellgrüne Bogenmitten-Evolvente der
dunkelgrünen Astroide benutzt, die selbst eine Astoide ist. Sie wird mit den hellgrünen Pfeilen mit den halben
Längen der dunkelgrünen gezeichnet. Die Längen betragen also 1/8 und 3/8. Das Triphil entsteht als Spur der
Spitze vom weiß gefüllten Pfeil mit der Länge 3/4, der an den Spurpunkt der Evolvente angesetzt ist und die
Richtung des Durchmessers vom Gangkreis der -2-Zykloide vom Radius 1/2 hat. Der Pfeil trifft das Triphil
an der Spitze unter einem Winkel von 90°. Das Triphil ist die Evolvente der dunkelgrünen Astroide durch eine
Spitze. Es unterscheidet sich von der Ellipse mit den Halbachsenlängen 1 und 0,5, hat aber auch Gemeinsam=
keiten damit. Denn diese Ellipse ist Evolvente der Kurve, die aus der dunkelgrünen Evolvente dadurch entsteht,
dass man sie in x-Richtung mit dem Faktor 0,75 streckt und in y-Richtung mit dem Faktor 1,5.

Tangenten-Vielecke beim Triphil
Das gleichseitige Dreieck mit der Wurzel aus 27/4 als Seitenlänge kann so um das Triphil gedreht
werden, dass dabei alle Seiten berühren. Dabei bewegt sich die Mitte des Dreiecks auf einem Kreis
mit dem Radius 1/4. Der Spurpunkt des Triphils ist die Spitze eines Pfeilzugs aus den hellgrünen
Evolventen-Pfeilen mit den Längen 1/8 und 3/8 und dem weiß gefüllten Pfeil mit der Länge 3/4. Der
weiße Pfeil dreht sich gegenläufig zum langen hellgrünen Pfeil mit gleichem Geschwindigkeits-Betrag.
Der kurze hellgrüne Pfeil hat die dreifache Geschwindigkeit.

Auch das Gleichdick, das zu der {-5;+5}-Zykloiden gehört, ist ein Triphil. Das Triphil dieser Animation
zur {-2;+2}-Zykloide ist aber dadurch ausgezeichnet, dass jedes Tangenten-Vieleck, bei dem die Winkel
zwischen aufeinander folgenden Tangenten gleich groß sind, die gleiche Umfangslänge haben.

Triphil und {-2;+2}-Zykloide
Entsprechend wie das Steiner-Gleichdick dem Zykloidenpaar aus -3- und +3-Zykloide zugeordnet
ist, liegt das Triphil zwischen der -2- und der +2-Zykloide. Die +2-Zykloide entsteht als Spur eines
Gangkreises mit dem Radius 1/2, der außen am Rastkreis abrollt. Sie wird üblicherweise als Nephroide
(Nierenkurve) bezeichnet. Wenn P und Q entsprechende Spurpunkte der -2- und der +2-Zykloide sind,
dann liegt der Punkt R, der die Strecke PQ im Verhältnis 3 : 1 = (2+1) : (2-1) teilt, auf dem Triphil.
Die Verbindungsgerade von P und Q ist stets Tangente an die dunkelgrüne Astroide, die wir auch als
{-2;+2}-Zykloide bezeichnen. Ihr Berührungspunkt S teilt die Strecke PQ außen im Verhältnis -3 : 1.
S ist also der vierte harmonische Punkt zu P, Q und R.