Es lebe die Geometrie!

Großkreis-Kachelung, die durch Spiegelungen an den Seiten
aus einem Kreis-Dreieck mit Winkeln 90°, 60° und 60° erzeugt wird

Unter einer 'Großkreis-Kachelung' verstehen wir eine Kachelung der Kugel vom Radius 1, bei
der alle Kachel-Seiten aus Großkreis-Bögen bestehen, oder das Bild dieser Kachelung bei einer
stereographischen oder gnomischen (auch geodätisch genannten) Projektion. Diese Projektionen
werden unten erklärt. Ein Großkreise ist die Schnittkurven der Kugel mit einer Ebene durch den
Kugel-Mittelpunkt. Das Bild der Kachelung bei der stereographischen Projektion nennen wir
'Poincare-Modell' der Kachelung und das bei der gnomischen Projektion 'Klein-Modell'. Winkel
werden auf der Kugel und im Poincare-Modell euklidisch gemessen und im Klein-Modell mit einem
nicht-euklidischen Maß, das unten erklärt wird. Im Poincare-Modell sind die Kachel-Seiten wie im
Kugel-Modell in der Regel Kreisbögen, im Klein-Modell aber stets geradlinig.

Den drei Modellen ist gemeinsam, dass die Summe der Innenwinkel in jeden Dreieck größer als 180°
ist. Dies steht im Gegensatz zu Kachelungen der hyperbolischen Geometrie, bei denen die Summe
dieser Innenwinkel stets kleiner als 180° ist. Die hyperbolische Kachelung ist auf der Kugel z. B. mit
Kreisen parallel zur z-Achse realisierbar und auch hier sind die stereographische und die gnomische
Projektion sinnvoll (siehe dazu 'Kreise auf der Kugel') Sowohl bei der hyperbolischen als auch der
elliptischen oder Großkreis-Kachelung wird der Inhalt der Dreiecksfläche durch den Betrag der
Differenz von der Innenwinkelsumme und 180° bestimmt. Im Unterschied zur Großkreis-Kachelung
füllt eine hyperbolische Kachelung aber die Ebene oder die Kugel nie vollständig aus (es sei denn, man
verwendet Hyperbelbögen an Stelle von Kreisbögen).

Wir betrachten hier nur durch Nachbar-Bewegungen erzeugte Dreiecks-Kachelungen, bei denen die
Seiten der Kacheln von 1 bis 3 oder von -1 bis -3 durchnummeriert sind. Die Nummern sind negativ,
wenn ihre Beträge im Uhrzeigersinn aufeinander folgen, bei positiven Nummern folgen sie gegen den
Uhrzeigersinn aufeinander. Eine Bewegung ist hier eine Abbildung, bei der die Beträge entsprechender
Winkel-Größen, Strecken-Längen und Seiten-Nummern im Bild und im Urbild gleich sind. Dabei
unterscheiden sich die Maß-Bestimmungen der Großkreis-Geometrie zum Teil von denen der
euklidischen und der hyperbolischen Geometrie. Die Vorzeichen von Winkel-Größen und Seiten-
Nummern ändern sich, wenn die Bewegung ungerade ist, also durch Hintereinanderschaltung einer
ungeraden Anzahl von Kreis-Spiegelungen entsteht. Eine Kachelung wird durch Nachbar-Bewegungen
erzeugt, wenn zu jeder Kachel K0 jede Nachbar-Kachel K1 Bild von K0 bei einer Bewegung ist.
Wenn dabei die Seite mit der positiven Nummer i in einer Ausgangskachel K0 bei der Nachbar-Kachel
K1 die Nummer hat, dann bezeichnen wir die Folge der Zahlen als 'Signatur' der Kachelung. Durch
Hintereinanderschaltung von Nachbar-Bewegungen darf es nicht vorkommen, dass sich Ausgangs- und
End-Kachel im Innern überdecken, es sei denn sie stimmen in ihrer Punktmenge und ihren Seiten-Nummern
überein.

Bei Großkreis-Kachelungen sind die Kombinations-Möglichkeiten für Innenwinkel-Größen der Dreiecke
wesentlich kleiner als bei hyperbolischen Kachelungen. Wenn nämlich die Kachelung durch Spiegelungen
an den Seiten erzeugt wird, die Signatur also -1-2-3 ist, dann muss für jede Innenwinkel-Größe gelten:
mit einer natürlichen Zahl n >1. Denn andernfalls würde es an einer Ecke des Dreiecks zu
Überlappungen kommen. Da aber die Summe der Innenwinkel größer als 180° ist, sind nur folgende
Kombinationen möglich:
Zwei 90°-Winkel und ein Winkel der Größe mit natürlichem k > 1.
90°, 60° und 60°
90°, 60° und 45°
90°, 60° und 36°

Im ersten Fall mit zwei rechten Winkel ergibt sich ein Kreisbogen-Dreieck wie es z. B. bei der Erdkugel
durch Bögen auf zwei Meridianen und dem Äquator realisiert ist. Alle Dreiecke der Kachelung haben dann
den Nordpol oder den Südpol als Eckpunkt. Die nächsten drei Fälle mit mindestens einem Innenwinkel von
60° sind geometrisch reichhaltiger. Sie zeigen einen Zusammenhang mit den platonischen Körpern, nämlich
im zweiten Fall mit dem Tetraeder und dem Oktaeder, im dritten mit dem Würfel und dem Oktaeder und im
vierten mit dem Ikosaeder und dem Dodekaeder. Den Spiegelungen an den Dreiecksseiten entsprechen die
Spiegelungen an den Symmetrie-Ebenen dieser Körper. Dies soll auf dieser Seite für die Tetraeder-
Kachelung gezeigt werden und auf den folgenden Seiten für die Würfel- und die Ikosaeder- Kachelung.

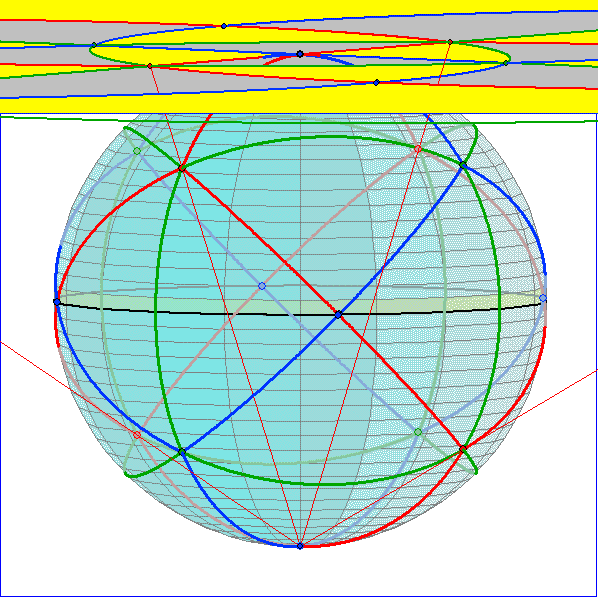
Das Bild 1 der Gleitschau zeigt den Zusammenhang zwischen der Tetraeder-Kachelung in der Ebene
und im Raum, Die Punkte der Kugel mit dem Radius 1 (Einheitskugel) werden vom Südpol (0 ; 0 ; -1)
auf die Tangentialeben E im Nordpol (0 ; 0 ; 1) projiziert (stereographische Projektion). Entsprechende
Punkte in der Ebene und der Kugel liegen also mit dem Südpol auf einer gemeinsamen Geraden. Das
Bild eines Punktes (x ; y ; z) der Kugelfläche hat darum die Koordinaten . Der schwarz
gezeichnete Äquator der Kugel hat darum als Bild den Kreis C um den Nordpol mit dem Radius 2, der
in den folgenden Bildern der Kachelung in E ebenfalls schwarz eingezeichnet ist. Damit auch der Südpol
eine Entsprechung für die Bild-Ebene hat, ergänzt man E durch einen künstlichen Punkt U, der als
'unendlich ferner Punkt' bezeichnet wird und der auf allen Bildern der Kugel-Kreise durch den Südpol
liegt. Die so ergänzte Ebene E wird als 'konforme Ebene' bezeichnet. Die durch stereographische
Projektion entstandene Kachelung in der Ebene E nennen wir 'Poincare-Modell' der Tetraeder-Kachelung.
Die Kachel-Seiten sind auch hier Kreisbögen, da die stereographische Projektion Kugel-Kreise in Ebenen-
Kreise abbildet. Wenn auf einem Kreis eine Kachel-Seite liegt, dann ist jeder Kreispunkt Punkt einer
Kachel-Seite. Dies ist typisch für Kachelungen, bei der alle Nachbar-Bewegungen Seiten-Spiegelungen
sind.

Jeder Seite-Kreisbogen auf der Kugel ist Teil eines Großkreises, der sich als Schnitt der Kugelfläche mit
einer Ebene durch den Ursprung ergibt. Jeder Seiten-Kreis auf der Kugel enthält darum mit jedem seiner
Punkte auch den Antipoden (Gegenpunkt) auf der gleichen Ursprungsgeraden. Da dem schwarzen Äquator
bei der stereographischen Projektion der Kreis C entspricht und die Äquatorebene zur Tangentialebene E
parallel ist, werden Antipoden des Äquators auf Schnittpunkte von C mit einer Durchmesser-Geraden
abgebildet, die wir 'Antipoden von C' nennen. Da jede Ebene durch die Kugelmitte den Äquator in einem
Antipodenpaar schneidet, gehen alle Seiten-Kreise im Poincaré-Modell durch ein Antipodenpaar auf C.
Wir bezeichnen einen Kreis durch ein Antipodenpaar auf C als 'Großkreis' des Poincaré-Modells. Wenn
M = (a ; b ; 1) der Mittelpunkt eines Großkreises ist, dann ist sein Radius. Die Gleichung
des Kreises ist darum oder . Die
Mittelpunkte aller Großkreise durch den gleichen Punkt A(x ; y ; 1) liegen darum auf einer Geraden g, die
orthogonal zur Verbindungsgeraden des Nordpols (0 ; 0 ; 1) mit A ist. Wenn r der Abstand des Punktes A
vom Nordpol ist, dann hat g vom Nordpol den signierten Abstand . Der Fußpunkt des Lots vom
Nordpol auf g ist der Mittelpunkt von A und seines Antipoden. Wir nennen g 'Großkreis-Zentrale' von A.

Der Ebenen-Spiegelung am Äquator entspricht in E die Spiegelung an C. Wenn darum A und B Antipoden
der Kugelfläche sind mit den Bildern A' und B' bei der stereographischen Projektion, dann dann ergibt sich
B' in der Tangentialebene E aus A' durch Hintereinanderschaltung der Spiegelung an C mit der Spiegelung
am Mittelpunkt von C. Wir bezeichnen diese Hintereinanderschaltung als 'Antipoden-Abbildung in E'. Das
Bild eines Punktes (x ; y ; 1) in E bei der Antipoden-Abbildung ist der Punkt .

Konstruktiv ergibt sich der Antipode B von A im Poincaré-Modell folgendermaßen: Der Großkreis k mit
Zentrum A schneide des Äquator in S. Dann ist B der gemeinsame Punkt der Tangente in S mit der
Geraden h durch A und den Nordpol. Der Kreis um B durch S ist dann ein zu k orthogonaler Großkreis.
Seine Schnittpunkte mit h sind die 'Pole' P1 und P2 von k. Bei der stereographischen Projektion sei K die
Ebene durch die Kugelmitte, deren Bild k ist. P1 und P2 sind dann die Bilder der Punkte der Kugelfläche
auf der Geraden, die auf K in der Kugelmitte senkrecht steht. Diese Punkte sind die 'Pole' des zu K
gehörigen Großkreises im Kugel-Modell.


Das Bild 2 der obigen Gleitschau zeigt das Poincaré-Modell der Kachelung in Bild 1. Der grauen Kachel
mit dem Eckpunkt im Ursprung im ersten Quadranten entspricht auf der Kugel das Dreieck mit dem blauen
Eckpunkt im Nordpol, das zum Betrachter hin gerichtet ist.

Zum Teil haben die Kacheln im Poincaré-Modell geradlinige Seiten. Man deutet sie als Kreisbögen mit
unendlich großem Radius. Acht der 32 Kacheln haben sogar zwei geradlinige Seiten. Davon haben vier
Kacheln nur zwei Eckpunkte im Endlichen, weil der dritte Eckpunkt U ist.

Benachbarte Kacheln gehen durch Spiegelungen an Kachel-Seiten auseinander hervor. Bei der Kugel-
Kachelung werden sie durch euklidische Spiegelungen an Ebenen durch die Kugel-Mitte O bewirkt, da die
Seiten alle auf Großkreisen liegen. Die den Seiten-Spiegelungen der Kugel entsprechenden Spiegelungen in
E sind Kreis-Spiegelungen. Sie sind also keine euklidischen Bewegungen, da sie den euklidischen Abstand
von Punkten nicht erhalten. Einen hier geeigneten Abstands-Begriff kann man aber in folgender Weise
definieren:

Für Punkte P und Q auf der Kugelfläche sei der nicht-euklidische Abstand durch die Länge des kürzeren der
beiden Großkreis-Bögen zwischen P und Q gegeben, und für die Bilder P' und Q' bei der stereographischen
Projektion habe der Abstand den gleichen Wert. Dies ist also der Arcuscosinus-Wert vom Skalarprodukt der
Koordinaten-Tripel von P und Q. Wir bezeichnen diesen nicht-euklidischen Abstand als 'Bogen-Abstand'.

Als Winkelmaß für Großkreise und ihre Bilder bei der stereographischen Projektion übernimmt man das
euklidische Winkel-Maß.

Die Kachel-Seiten geben durch die Farben rot, grün und blau die Beträge der zugeordneten Seiten-
Nummern 1, 2 und 3 an. Die Seiten haben einen Durchlauf-Richtung gegen oder im Uhrzeigersinn,
der bei der roten Seite durch einen Halb-Pfeil angezeigt ist. An der Spitze der Halb-Pfeile liegen die
Eckpunkte mit der Nummer 1. Bei der Kreis-Spiegelung an einer Seite zur Erzeugung der Nachbar-
Kachel ändert sich die Orientierung von 'positiv' (gegen den Uhrzeigersinn) in 'negativ' oder umgekehrt.
Negativ orientierte Kacheln sind gelb gezeichnet. Die Antipoden-Abbildung in E bildet die Punktmenge
jeder Kachel auf die Punktmenge einer gleich orientierten Kachel ab.

Die Bilder 3, 4 und 5 stellen die stereographische Projektion mit Seiten der Kugel-Kacheln in jeweils
nur einer Farbe dar. In Bild 3 ergeben die roten Kreisbögen eine Kachelung der Kugel oder von E mit
vier Dreiecken mit den Innenwinkel 120°. Als Signatur ist hier 123 geeignet. Die Nachbar-Bewegungen
sind dann Spiegelungen an den Seitenmitten, die in Bild 1 und 6 blau gezeichnet sind. Diese Spiegelungen
ergeben sich dadurch, dass man zwei Spiegelungen an orthogonalen Kreisen durch die Seitenmitte
hintereinander schaltet. Entsprechendes wie in Bild 3 gilt auch für die blauen Kreisbögen in Bild 5. Die
grünen Linien in Bild 4 gehören zu einer Kachelung aus sechs Vierecken, bei der die Signaturen 1234
und 2143 möglich sind.

Bild 6 und 7 zeigen die Tetraeder-Kachelung auf der Kugel in verschiedenen Ansichten.

Die Bilder 8 bis 13 verdeutlichen die Beziehung zu platonischen Körpern. Die Verbindungen der
roten Punkte durch Strecken ergeben die Kanten eines Tetraeders (Bild 8 und 11), ebenso die
Verbindungen der grünen Punkte (Bild 9 und 12). Dabei liegen die Kanten-Mitten auf den Geraden
durch die Kugelmitte und die blauen Punkte. Das Oktaeder in Bild 10 und 13 hat die blauen Punkte
als Eckpunkte. Dabei sind die Mitten der Oktaeder-Flächen mit der Kugel-Mitte und einem roten
oder grünen Punkt kollinear.

Die Bilder 14 und 15 zeigen komplementäre Teil-Kachelungen im Poincare-Modell mit der
Eigenschaft, dass zu jeder Kachel einer der Teil-Kachelungen die zugehörige Antipoden-Kachel
in der anderen Teil-Kachelung liegt.

Bild 16 zeigt eine Kachelung in E, die dadurch entsteht, dass die Tetraeder-Kachelung auf der Kugel
nicht durch stereographische Projektion auf die Ebene E übertragen wird, sondern durch Projektion
mit dem Kugelmittelpunkt O als Zentrum an Stelle des Südpols. Der Bildpunkt eines Punktes P der
Kugel ist also der Schnittpunkt P' der Geraden g durch P und O mit der Ebene E, falls dieser existiert.
Andernfalls, wenn also g parallel zu E ist, ergänzt man E um einen "unendlich fernen Punkt" auf g. Da
dies für jede zu E parallele Geraden gemacht werden muss, sind unendlich viele unendlich ferne Punkte
nötig. Diese fasst man zu einer " unendlich fernen Geraden" von E zusammen, welche also die Bildmenge
des Äquators darstellt. Die so erweiterte Ebene E nennt man 'projektiv'. Bemerkenswert ist bei dieser
Projektion, die 'gnomisch' oder auch 'geodätisch' genannt wird, dass Antipoden der Kugel auf den
gleichen Bildpunkt abgebildet werden. Wenn man dabei die Maßbestimmungen für Winkelgrößen und
Abstände von der Kugel auf E überträgt, erhält man in E ein Modell der 'elliptischen Ebene', das wir
'Klein-Modell' der elliptischen Ebene nennen. Ein anderes Modell der elliptischen Ebene ergibt sich in
der Kugelfläche selbst, wenn man hier jeden Punkt mit seinem Antipoden identifiziert. Die durch
gnomische Projektion in der Ebene E entstandene Kachelung nennen wir 'Klein-Modell' der Tetraeder-
Kachelung. Entsprechend wie beim Poincaré-Modell gilt auch hier: Wenn auf einer Gerade eine
Kachel-Seite liegt, dann liegt jeder Punkt der Geraden auf einer Kachel-Seite.

Der schwarze Kreis C hat auch in Bild 16 den Radius 2 und den Nordpol als Mittelpunkt. Für das
Klein-Modell der elliptischen Ebene hat er folgende Bedeutung: M sei der Mittelpunkt eines Kreises,
der sich als stereographisches Bild eines Großkreises k ergibt, und S der euklidische Mittelpunkt
zwischen Nordpol und dem Antipoden M' von M. Dann ist S der Fußpunkt des Lots vom Nordpol
auf das Bild g von k bei der gnomischen Projektion. Man erhält darum diesen Scheitelpunkt S von g,
indem man M zunächst an C spiegelt und auf das Bild die Streckung mit dem Faktor -0,5 und dem
Nordpol als Zentrum anwendet. Für M = (a ; b ; 1) ist also S = , und genau
für die Punkte (x ; y ; 1) auf g gilt die Gleichung . Die zugehörige Großkreis-Ebene
hat dann die Gleichung . Wenn P und Q die Bilder desselben Kugelpunktes bei
stereographischen bzw. der gnomischen Projektion sind und P die Koordinaten (x ; y ; 1) hat, dann
ist Q = , wobei der Nenner die Potenz von P bezüglich des

Kreises C ist. Wenn umgekehrt Q die Koordinaten (x ; y ; 1) hat, dann ist
P = 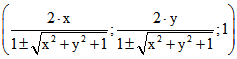, wobei die verschiedenen Vorzeichen berücksichtigen,
dass stets beide Punkte eines Antipoden-Paars im Poincare-Modell den gleichen zugehörigen Punkt
im Klein-Modell haben.

Die Animation zeigt in einem parallelen Ablauf den Aufbau der Tetraeder-Kachelung im
Poincare-Modell und auf der Kugel. Die graue Ausgangskachel in E hat die Eckpunkte
, und .
Der Kreis-Mittelpunkt zum grünen Bogen der Seite 2 hat die Koordinaten .

Diese Animation soll den Zusammenhang zeigen, der durch die Antipoden-Abbildung gegeben ist.
Die Antipoden-Kachel K0' zur grauen Ausgangskachel K0 entsteht aus K0, indem man nacheinander
an folgenden Seiten spiegelt: 312312. Wir nennen eine derartige Folge 'Abbildungskette'. Der Aufbau
einer Teil-Kachelung wird dann im linken Bild ausgehend von K0 durch die Kette
1212132321
beschrieben. Im rechten Bild ergibt sich die Folge der Antipoden-Kacheln aus K0' durch die Kette
3232312123.
Die Zahlen 1 und 3 sind also vertauscht.

Die Animation stellt den Zusammenhang zwischen dem Poincaré-Modell und dem Klein-Modell
der Tetraeder-Kachelung dar. Da im Klein-Modell jeder Kachel zwei Kacheln im Poincaré-Modell
entsprechen, die Antipoden voneinander sind, hat das Klein-Modell nur halb so viele Kacheln wie das
Poincaré-Modell.

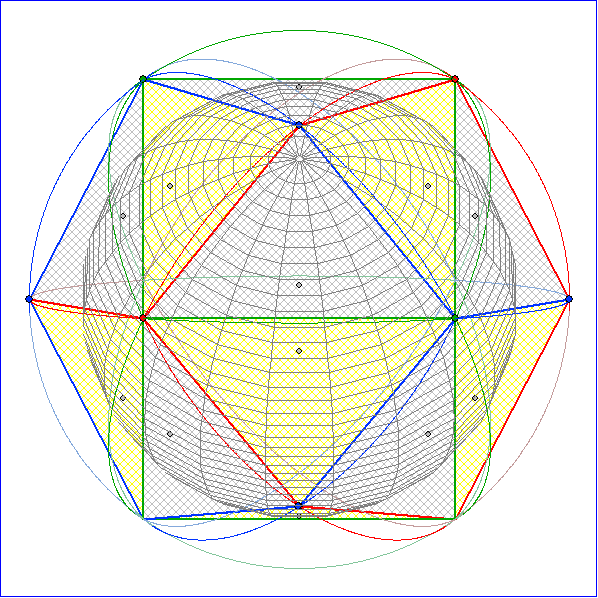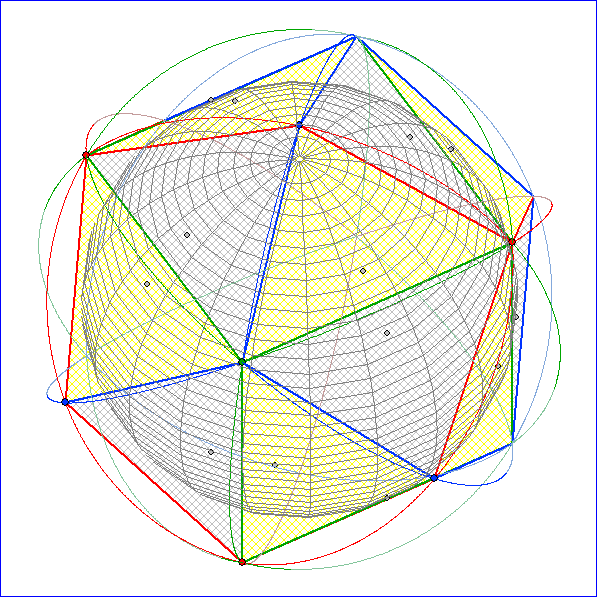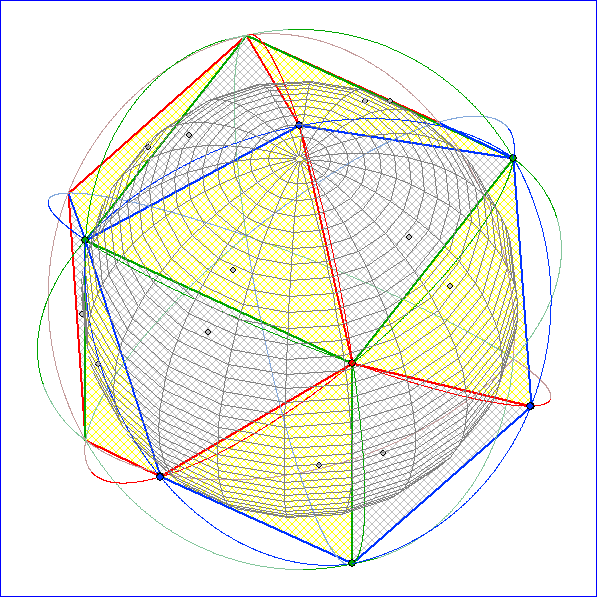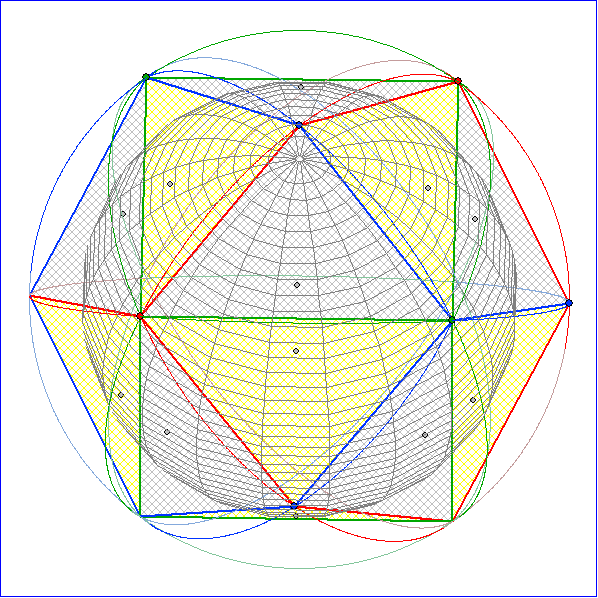
Die Animation zeigt das Kachelungs-Polyeder zur Tetraeder-Kachelung. Es entsteht dadurch, dass
die Kreisbögen der Kachelung im Kugel-Modell durch Strecken ersetzt werden. Es ergeben sich
lauter kongruente gleichschenklige Dreiecke. Die roten und die blauen Strecken haben die Länge
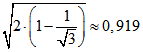und schließen einen Winkel mit der Größe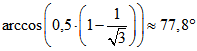
ein. Alle Dreiecke berühren in den grauen Umkreis-Zentren der Dreiecke eine Kugel mit dem Radius
.
Das Polyeder hat also bemerkenswerterweise nicht nur eine Umkugel, sondern auch eine Inkugel.
Diese Eigenschaft hat es mit den platonischen Körpern gemeinsam, die aber zusätzlich noch eine
Kantenkugel haben, die also alle Kanten berührt.

Die Bilder 1 bis 4 zeigen das Kachelungs-Polyeder mit und ohne Inkugel bzw. mit und ohne verdeckte
Kanten. In den Bildern 5 bis 7 sind jeweils die roten bzw. grünen bzw. blauen Eckpunkt so verbunden
worden, dass Kanten-Netze platonischer Körper entstehen. In Bild 8 sind die Umkreise der grauen
Dreiecke hinzugefügt.