Es lebe die Geometrie!

Winkelhalbierende im 6-Rechteck des hyperbolischen Raumes

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

-->'Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum II'
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_II.pdf

Das 6-Rechteck des hyperbolischen Raums ist gleich definiert wie für den euklidischen Raum,
nämlich als räumliches 6-Eck, bei dem die in den Eckpunkt zusammentreffenden Geraden
orthogonal sind, hier hyperbolisch orthogonal. Wenn man von drei paarweise nicht komplanaren
Geraden ausgeht und zu jedem Paar dieser Geraden eine der beiden zueinander polaren
Achsen auswählt, bilden die Lotfußpunkte dieser Achsen ein hyperbolisches 6-Rechteck.

Diese Animation entspricht der für euklidische 6-Rechtecke auf der Seite
' euklidische Raumgeraden>Winkelhalbierende'.
In den vier Phasen der Animation werden die vier Möglichkeiten für Achsen von je drei der
Winkelhalbierenden in einem hyperbolichen 6-Rechteck ABCDEF im Innern der Einheits-Kugel K
dargestellt. Die Kanten von ABCDEF wurden bis zu den weiß gefüllten Punkten auf K verlängert. Das
6-Rechteck ist analog zu einem Dreieck ACE , das unten rechts im Bild gezeigt wird. Zu den Kanten
AB, CD und EF wurden die Mittenkreuze eingezeichnet, und zwar beim inneren hyperbolischen Mittelpunkt
der jeweiligen Kante. Die graue und die schwarze Strecke sind hyperbolisch orthogonal. Die Ausrichtung
dieser Strecken ist in allen vier Phasen der Animation gleich. Die grau gezeichnete Strecke gibt die Richtung
der Winkelhalbierenden an, die in der jeweiligen Phase unter den beiden Winkelhalbierenden durch den
Mittelpunkt ausgewählt wurde. Die mit einem gelben Mittelstreifen gezeichnete Achse dreier Winkelhalbierender
entspricht im Analogie-Dreieck unten rechts dem Inkreis- oder einem Ankreis-Zentrum.

Der Tatsache, dass diese Zentren von allen drei Seiten des Analogie-Dreiecks den gleichen Abstand haben,
entspricht beim 6-Rechteck der Gleichheit der Zahlen-Paare an den dunkelrot, dunkelgrün und dunkelblau
gezeichneten Lotverbindungen der Winkelhalbierenden-Achse mit den Kanten-Geraden zu DE, BC und FA.
Dies Zahlenpaar gibt das Maß für das Geraden-Paar an, auf das die gelben Pfeile zeigen. Es setzt sich aus
einer Winkelgröße und aus einem Abstandsmaß zusammen.

Zur Berechnung dieser Maße gehen wir von k-normierten Tripeln komplexer Zahlen s, u und w aus, die zu den
Geraden der Kanten BC, DE und FA gehören. Die Tripel dreier Winkelhalbierenden sind dann ,
und , und das Tripel der gemeinsamen Achse ist der k-normierte Term zu ,
also . Wenn man jeweils zwei der drei Tripel s, u und w mit -1 multipliziert, erhält man die anderen
drei Achsen. Bei dem Zahlen-Paar des Abstandsmaßes ist die zweite Zahl der hyperbolische Abstand d der
Lotfußpunkte. Dieser Abstand wurde auf der Seite ' hyperbolische Raumgeraden>Orthogonalität' erklärt.
Bei dem Maß für das Geradenpaar zu s und m ist die erste Zahl , wobei
den Realteil der komplexen Zahl angibt. Die Zahl ist in der Grad-Schreibweise angegeben, wobei
das Zeichen ° für den Faktor steht. Für die komplexe Zahl gilt , denn
. Es ist dies die gleiche
Beziehung, die am Schluss der Seite ' euklidische Raumgeraden>Mittelsenkrechte' dargestellt wurde.

Die Animation zeigt, dass es längs jeder Winkelhalbierenden-Achse drei hyperbolische Schraubungen
gibt, welche die Kanten-Geraden von DE, BC und FA in die jeweils folgende dieser drei Kanten-Geraden
abbilden. Bei jeder dieser Schraubungen wird eine zur Achse g orthogonale Gerade h in eine zu g orthogonale
Gerade h* abgebildet. Ihre k-normierten Tripel seien y und y*. Das Paar aus Winkelgröße und Abstand zum
Geradenpaar (h;h*) sei . Dann ist .

Zur Berechnung der Schraubungen:

Sei (u ; v) Tripel-Paar der Geraden g in Plücker-Koordinaten mit (fg(u;v);gg(u;v)) = (1;0) . Dann ist k-normiertes Tripel
komplexer Zahlen. Sei G(u;v) die schiefsymmetrische Plücker-Matrix (nach Julius Plücker (1801-1868))
,
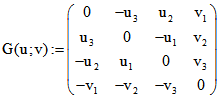GS(u ; v) die Matrix, die aus G(u ; v) dadurch entsteht, dass die letzte Spalte mit -1 multipliziert wird,
und
.
Dann wird ein Punkt P mit dem Quadrupel p durch die zugehörige Schraubung in den Punkt mit dem
Quadrupel p.M abgebildet und es gilt das Additions-Gesetz .
Wir nennen diese Abbildung . Siehe dazu auch die Seite 'elliptische Raumgeraden>
Schraubungen'. Eine entsprechende Matrix mit komplexen Zahlen ist die Matrix ,
die am Schluss der Seite 'hyperbolische Raumgeraden> Kugelviereck2' angegeben ist.

Die Wirkung der Schraubung für ein beliebiges Geraden-Tripel s wird beschrieben durch
mit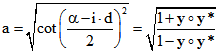
für die oben genannten Tripel y und y*. Siehe dazu Satz 48 in dem im Kopf dieser Seite genannten Text.

Die Zwischenzustände bei dieser Schraubung ergeben sich dadurch, dass und d mit dem gleichen Faktor
zwischen Null und Eins multipliziert werden. Dadurch kann die Spur der Endpunkte der Kugelsehne auf K
gezeichnet werden.

Hyperbolische Schraubungen und spezielle Relativitäts-Theorie :

Die speziellen Relativitäts-Theorie beschreibt den Zusammenhang zwischen Messungen des Zeitpunkts t
und dreier Ortskoordinaten eines Ereignisses (z.B. eines Licht-Blitzes) in verschiedenen Bezugs-Systemen
S(x;y;z;t) und S'(x';y';z';t'), wenn S' (Zug auf Schiene) sich z. B. mit der Geschwindigkeit v auf der
x-Achse von S (Bahnhof bei x = 0) entfernt. Zwischen den Koordinaten gilt dann die Gleichung
, wobei und c die
Lichtgeschwindigkeit ist. Mit Hilfe einer Matrix L ergibt sich, wenn die Maßeinheiten so gewählt werden,
dass c = 1 ist: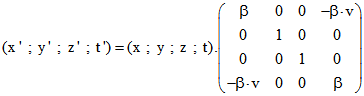


Eine L entsprechende Matrix wird aus der oben genannte Matrix M(0;d) zur , wenn g
die x-Achse mit dem Tripel u = (1 ; 0 ; 0) ist, nämlich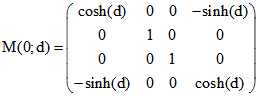

Man identifiziert und , also und
. Wenn sich auf der x-Achse ein System S'' gegenüber S' mit der Geschwindigkeit
bewegt, dann bewegt sich S'' gegenüber S mit der Geschwindigkeit .
Die Additions-Eigenschaft der Abstände längs einer Geraden in der Geometrie des hyperbolischen
Raums entspricht hier also der Additivität der Artanh-Werte von System-Geschwindigkeiten. Diesen
Zusammenhang zwischen Schraubungen des hyperbolischen Raumes und den Lorentz-Transformation
der speziellen Relativitäts-Theorie gibt es nicht nur für die x-Achse, sondern für alle endlichen Geraden des
dreidimensionalen Raums, und zwar für alle Werte der Verschiebungslänge d und auch des Drehwinkels .
Die Matrizen werden nicht nur für die Transformation von Quadrupeln von Messwerten für Ortskoordinaten
und Zeiten in ein anderes Mess-System benutzt, sondern z. B. auch für die Transformation von Messwerten
für Impulse und Energien.

Abstände von Punkten werden in der Relativitäts-Theorie allerdings nicht hyperbolisch gemessen. Die
Gemeinsamkeiten ergeben sich daraus, dass für jede Matrix L einer Lorentz-Transformation gilt:
Für das Transformations-Ergebnis (x';y';z';t') = (x;y;z;t).L eines Quadrupels (x;y;z;t) ist
.
Diese Gleichung gilt auch für die Punkt- oder Ebenen-Quadrupel in der Geometrie des hyperbolischen
Raums, wenn sie mit einer Schraubung abgebildet werden. Die vierte Komponente dient dabei aber nur
zur Erfassung der unendlich fernen Punkte. Dafür wären eigentlich nur die Zahlenwerte 0 und 1 zur
Unterscheidung der unendlich fernen und der endlichen Punkte nötig. Dass alle reellen Zahlen zugelassen
sind, führt jedoch zu rechnerischen Vereinfachungen.