Es lebe die Geometrie!

Flächeninhalte bei k-Zykloiden

Die k-Zykloide ist in komplexer Darstellung der Graph der Funktion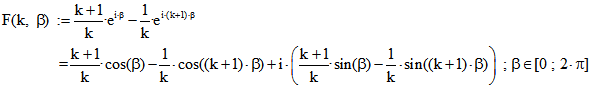
.
Mit und kann
darum der Inhalt der Fläche, die von der k-Zykloiden eingeschlossenen wird, mit dem Stieljes-Integral
berechnet werden. Das ergibt diese Liste von Werten:




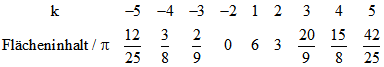
In den folgenden Animationen sollen geometrische Zusammenhänge zwischen Zykloiden- und Rollkreis-
Flächen untersucht werden. Dabei sind die Inhalte der hellblauen und der karierten Flächen proportional
zueinander. Dies ist darin begründet, wie sich die Richtungsänderung der dunkelblauen Sehne des
kleinen Rollkreises zwischen dem roten Punkt P und dem hellblauen Punkt Q auf die Änderung dieser
beiden Flächen auswirkt. Die Sehne PQ liegt auf der Tangente in P, weil Q das Zentrum des großen
Rollkreises ist, auf dessen Durchmesser sich P bewegt. Die Änderung der hellblauen und der karierten
Fläche bei der Bewegung von P ist in einem Teil der Animationen an zwei schmalen Dreiecken in
mittlerem Blau und im karierten Grau dargestellt, bei denen PQ eine gemeinsame Seite ist. Wenn die
Winkelgröße des blauen Dreieck bei P mit bezeichnet wird und die des grauen Dreiecks mit ,
dann ist ihr Flächeninhalt näherungsweise bzw. , wobei die Winkel im Bogenmaß
bestimmt sind. Der Fehler, der dabei gemacht wird, verschwindet im Grenzfall, wenn die Dreiecke
immer schmaler gemacht werden. Bei der Rollbewegung verhält sich darum die Flächen-Änderung
der blauen Fläche zu der Flächen-Änderung der karierten wie zu (für Winkelgrößen gegen
Null). ist die Richtungswinkel-Änderung der Tangente in P und die Änderung des Winkels
zwischen der Strecke PQ und der Ursprungsgeraden durch Q und dem Berührpunkt von Roll- und
Gang-Kreis. Das Verhältnis der beiden Winkelveränderungen ist bei der Rollbewegung konstant, da
die Winkelgeschwindigkeiten der beiden roten Pfeile in einem festen Verhältnis stehen. Beim Durchlauf
eines halben Bogens einer k-Zykloide mit der Gleichung und Spitzen
ändert sich der Richtungswinkel des langen Pfeils um den Betrag von und der des kurzen Pfeils um
den Betrag von . Darum ändert sich dabei der Richtungswinkel der Tangente in P um den
Betrag von , während sich der Winkel zwischen der Strecke PQ und
der Ursprungsgeraden durch Q um verändert. Das Verhältnis der beiden Winkelveränderungen ist
demnach . Dies ist also auch das Verhältnis der Flächeninhalte der hellblauen und karierten Fläche
während des ganzen Rollvorgangs.

Diese Kardioide ist die 1-Zykloide mit der Gleichung . Das Verhältnis der Flächen=
inhalte der hellblauen und der karierten Fläche ist stets . Nach Durchlaufen des ganzen
Zykloidenbogens füllt die karierte Fläche den ganzen Rollkreis aus, hat also den Flächeninhalt
bei einem Gangkreis- und Rollkreis-Radius 1. Die hellblaue Fläche hat dann folglich den Inhalt .
Da der äußere Kreis den Radius 3 hat, beträgt der Inhalt der Flächeninhalt innerhalb der Kardioide
.

Für die -3-Zykloide (Steiner-Zykloide) mit der Gleichung ist das Verhältnis der
hellblauen zu karierten Fläche stets . Die hellblaue Fläche hat nach Durchlaufen eines
Zykloidenbogens 1/3 des Inhalts des Rollkreises. Darum ist die gesamtre Fläche im Innern der Zykloide
doppelt so groß wie der Rollkreis.

Hier wurden die k-Zykloiden mit der Gleichung für k = 4 und k = -4
gezeichnet. Nach Durchlaufen eines Zykloidenbogens ist der Inhalte der hellblauen Fläche für die
äüßere bzw. innere Zykloide bzw. mal so groß wie einer der beiden gleich
großen Rollkreise. Da der äußerste Kreis 36 mal so groß ist wie ein Rollkreis, ist der Inhalt der Fläche
innerhalb der 4-Zykloide 30 mal so groß. Der kleinste Kreis um den Ursprung hat den 4-fachen Inhalt
des Rollkreises. Darum ist das Innere der -4-Zykloide (Astroide) 6 mal so groß wie ein Rollkreis.
Jede der ovalen Flächen zwischen den Zykloidenbögen hat den Inhalt von 6 Rollkreisen.