Es lebe die Geometrie!

Kugelkreis-Dreiseite ohne Seitenschnittpunkte

--> Die Pseudosphäre und die hyperbolische Geometrie
https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Anders als in der euklidischen und der elliptischen Geometrie gibt es in der hyperbolischen Geometrie
nicht-triviale Dreiseite ohne Eckpunkte, auf die sich Sätze über Mittelsenkrechte, Seitenhalbierende,
Winkelhalbierende und Höhen übertragen lassen. In den folgenden vier Animationen wird das für die
vier Geradentypen im Rahmen der Kugelkreis-Geometrie dargestellt. Die zu diesen Z-'Geraden' gehörigen
Kugelflächen-Kreise liegen alle in Ebenen durch einen Punkt Z auf der z-Achse außerhalb der Kugel.
Ihre Bilder im Klein-Modell bzw. Poincare-Modell, die bei Zentralprojektion auf die Tangentialebene
im Nordpol mit Z bzw. dem Südpol als Zentrum entstehen, sind in den Animationen links bwz. rechts
oben eingezeichnet.

Das betrachtete Dreiseit wird durch drei Punkte in der Tangentialebene des Nordpols festgelegt, die
bei den Animationen unverändert bleiben. Sie wurden so gewählt, dass die Parallelen zur z-Achse durch
diese Punkte die Kugel nicht schneiden, dass aber die drei Ebenen durch Z und je zwei dieser Punkte
Schnittkreise mit der Kugel haben. Wir bezeichnen diese Seiten-Kreise mit a, b und c. Wenn Z sich auf
der z-Achse der Kugel aus großer Entfernung nähert, verkleinert sich der Abstand zwischen den Seiten-
Kreisen und sie schneiden sich dann. Wenn Z im Südpol liegt, liegt dieser auf allen drei Seiten-Kreisen;
die zugehörige Geometrie ist dann euklidisch.

Alle vier Animationen laufen nach dem gleichen Schema ab: Es gibt fünf Stops für verschiedene Positionen
von Z (die ersten beiden mit 360°-Flügen). Bei den ersten beiden Stops sind a, b und c paarweise getrennt,
beim dritten schneiden sich nur a und b nicht, beim vierten schneiden sie sich alle drei paarweise, und beim
fünften liegt der euklidische Fall vor.

Hier geht es um das Schneiden von Z-'Mittelsenkrechten'. Die Z-'Mittelsenkrechte' z.B. zu der Seite a
ist folgendermaßen definiert: bzw. seien die Schnittgeraden der Ebenen zu a und b bzw. a und c.
Dann gibt es in manchen Fällen eine Kugelkreis-Spiegelung , die in abbildet, wobei der Punkt
P außerhalb der Kugel in der Ebene mit dem Pol Z liegt. Dann ist der Kugelkreis mit dem Pol P die gesuchte
Z-'Mittelsenkrechte' von a. Diese Spiegelung gibt es immer dann, wenn und beide die Kugel entweder
in zwei Punkte schneiden oder beide nicht schneiden. Darum existieren drei Z-'Mittelsenkrechte' in den Fällen,
dass a, b und c paarweise getrennt sind oder sich paarweise schneiden. Die Ebenen dieser drei
Z-'Mittelsenkrechten' haben stets eine Gerade gemeinsam. Wenn sich darum zwei der Z-'Mittelsenkrechten'
schneiden, dann geht auch die dritte durch jeden Schnittpunkt; und die beiden gemeinsame Punkte liegen
auf einer Geraden m durch Z. Im Fall des paarweise Schneidens der Z-'Seitengeraden', wenn es also Eckpunkte
A, B und C gibt, existiert dazu ein Umkreis mit dem Pol auf m. In der Animation kommen bei allen Stops außer
dem dritten drei Z-'Mittelsenkrechte' vor. Beim zweiten Stop schneiden sie sich nicht. Die zugehörigen Geraden
im Klein-Modell haben dennoch einen gemeinsamen Punkt, der allerdings außerhalb des schwarzen Kreises
liegt, der das Bild des Kugelkreises mit dem Pol Z ist und die Punktmenge des klassischen Klein-Modells begrenzt.

Bei den Z-'Seitenhalbierenden' treten ähnliche Effekte auf wie bei den Z-'Mittelsenkrechten', weil in
beiden Fällen ein Punkt benötigt wird, der dem Mittelpunkt einer Seite entspricht. Man definiert
die Z-'Seitenhalbierende' von a in folgender Weise: sei die Schnittgerade der Ebenen von b und c.
sei die Schnittgerade der Ebenen von a und der Z-'Mittelsenkrechten' m zu a. Dann haben diese
beiden Schnittgeraden den Punkt Z gemeinsam und liegen darum in einer Ebene, deren Schnittkreis
mit der Kugel wir als Z-'Seitenhalbierende' von a bezeichnen. Wie bei den Z-'Mittelsenkrechten'
gibt es diese Z-'Seitenhalbierende' nur dann, wenn und entweder beide die Kugel nicht
treffen oder sie beide in zwei Punkten schneiden. Wenn es drei Z-'Seitenhalbierende' gibt, haben
sie stets zwei gemeinsame Schnittpunkte, deren Verbindungsgerade durch Z verläuft.

In einem Kugelflächen-Dreiseit abc existieren stets drei Z-'Höhen'. Es gibt also keine Ausnahmen wie
bei Z-'Mittelsenkrechten' oder Z-'Seitenhalbierenden'. Es sei die Schnittgerade der Ebenen von
b und c. Dann ist die Z-'Höhe' zu a der Schnittkreis der Ebene durch und den Pol von a. Die drei
Z-'Höhen' im Kugelflächen-Dreiseit haben immer eine gemeinsame Gerade durch Z. Wie bei den
Z-'Mittelsenkrechten' kann es aber vorkommen, dass diese Gerade die Kugel nicht schneidet. Dann
haben die Z-'Höhen' paarweise also keinen gemeinsamen Punkt. Die Bildkreise der Z-'Höhen' im
Klein-Modell schneiden sich dann in einem Punkt außerhalb des schwarzen Bildes des Kugelkreises
zu Z.

Eine Z-'Winkelhalbierende' zu einem Paar a, b von Kugelflächen-Kreisen ist ein Kugelfächen-Kreis mit
einem Pol P, dessen Spiegelung a in b abbildet. Wenn a und b sich in zwei Punkten schneiden, existieren
zwei derartige Z-'Winkelhalbierende', andernfalls nur eine. Es gibt stets drei Z-'Winkelhalbierenden'
eines Dreiseits abc mit zwei gemeinsamen Punkten, die mit Z kollinear sind. Auf der Verbindungsgeraden
liegen die Pole zweier Kreise, die a, b und c berühren.

Das letzten beiden Bilder der Gleitschau sollen den Zusammenhang zwischen den Bildern der Zentral-
Projektionen mit den Zentren S(0;0;-1) und für darstellen. Die Abbildung der
Punkte der Einheits-Kugelfläche K auf die Ebene E : z = 1 wird beim Zentrum Z auf der z-Achse für
kartesische Koordinaten-Tripeln durch 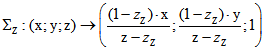bestimmt. Wir wenden
diese Abbildungs-Vorschrift nicht nur auf die Punkte von K, sondern auf alle Punkte (x;y;z) mit an.

Für hat folgende besondere Eigenschaften:

Es gibt für die Restriktion von auf E die Umkehr-Abbildung
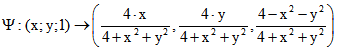, so dass also gilt.

bildet die Menge der Kreise A auf K, die nicht mit S inzidieren, bijektiv auf die Menge der Kreise
A' in E ab. Wenn P der Pol der Ebene von A bezüglich K ist, hat der Mittelpunkt von A' die Koordinaten . Die Menge der Kreise auf K, die mit S inzidieren, wird bijektiv auf die Menge der
Geraden in E abgebildet. Die euklidische Größe des Schnitt-Winkels zwischen zwei Kreisen A und B auf K
stimmt mit der euklidische Größe des Schnitt-Winkels der Bilder in E überein. Dieser Winkel unterscheidet
sich von dem Winkel zwischen den Schnitt-Ebenen von A und B mit K, da der Winkel zwischen A und B
in der Tangential-Ebene eines Schnittpunkts von A und B gemessen wird.

Die Gerade g durch die Pole P und Q bezüglich K zu Kreisen A und B auf K wird durch auf die Gerade g' durch die Mittelpunkte von A' und B' abgebildet. Wenn A' eine Gerade ist, betrachtet man als
Mittelpunkt von A' den unendlich fernen Punkt auf einer Orthogonalen von A'. Für Kreise A' und B' ist g'
die zugehörige Ähnlichkeits-Achse, auf der die Zentren der beiden Streckungen liegen, die A' in B' abbilden,
wobei diese Zentren die Strecke zwischen den Zentren von A' und B' innerlich und äußerlich im Verhältnis
der Radiusse von B' und A' teilen. Die Schnitt-Gerade der Ebenen von A und B ist bezüglich K die zu g
polare Gerade h. Wenn A' und B' Kreise sind, ist das -Bild von h die Potenz-Gerade (Radikal-Achse)
von A' und B', also die Gerade der Punkte R, deren Potenz zu A' und B' übereinstimmt. Dabei ist die Potenz
von R zu einem Kreis mit Zentrum M und Radius r gleich . g' und h' sind orthogonal. Der Polarität
der Geraden g und h im Raum mit der durch die Einheits-Kugel gegebenen Maß-Bestimmung entspricht also
bei den Bilder g' und h' die euklidische Orthogonalität in der Ebene E.

Wenn A', B' und C' drei Kreise mit nicht kollinearen Zentren sind, ist das -Bild des Schnittpunkts der
Ebenen zu A, B und C auf K der Potenz-Punkt (Radikal-Punkt) von A', B' und C', für den die Potenzen zu
A', B' und C' gleich sind. Dies ist also der Schnittpunkt der Potenz-Geraden zu A' und B', B' und C', sowie C'
und A'. Im Fall positiver Potenz ist er Mittelpunkt eines Kreise in E, der A', B' und C' orthogonal schneidet
und das -Bild des Kreises auf K ist, dessen Pol der Schnittpunkt der Ebenen von A, B und C ist.

Wenn A durch Spiegelung an B auf C abgebildet wird, sind die zugehörigen Pole kollinear und
folglich auch die Mittelpunkte von A', B' und C'. Die Spiegelung an B' bildet dann A' in B' ab. Dabei ist
der Mittelpunkt von B' Streckungs-Zentrum (Ähnlichkeits-Zentrum) einer der beiden Streckungen, die
A' in C' abbilden.

Mit diesen Grund-Eigenschaften der stereografischen Projektion kann nach dem Muster für die Konstruktion
des in der letzten Gleitschau dargestellten magenta-farbenen Inkreises ein altes Problem von Apollonios von
Perge (-265 bis -190) entwickelt werden, nämlich zu drei gegebenen Kreise in der Ebene einen Kreis zu
finden, der alle drei berührt. Dies soll in der folgenden Gleitschau dargestellt werden.

Zum Zusammenhang zwischen den Bildern bei der Poincare-Projektion und der Klein-Projektion:
Für ergibt sich mit ,
wobei für den Grenzfall der Nenner ist. Die Abbildung , die jedem Bildpunkt P
der Poincare-Projektion das entsprechende Bild Q der Klein-Projektion zuordnet, hat folgende Eigenschaften:

P und Q liegen auf einer Geraden durch den Punkt N(0;0;1).

Jeder Kreis mit dem Zentrum N wird auf einen Kreis um N abgebildet, dessen Radius nicht größer ist.

Jeder Kreis in E, der -Bild eines Kreise C auf K ist, dessen Ebene mit Z inzidiert, wird auf eine
Gerade abgebildet, die -Bild von C ist.

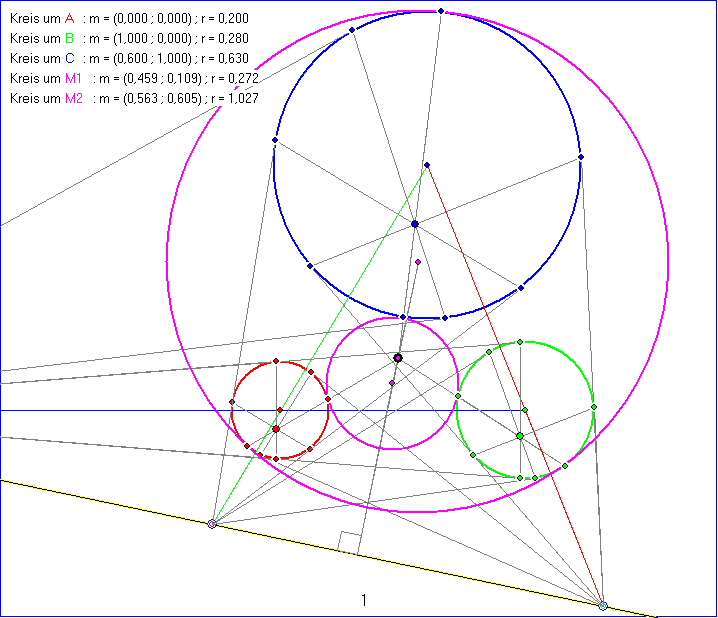
Das erste Bild der Gleitschau zeigt die drei gegebenen Kreise KA, KB und KC mit den Mittelpunkten A, B und
C, sowie die beiden Kreise K1 und K2 mit den Zentren M1 und M2, die KA, KB und KC innen bzw. außen
berühren. Der schwarze Kreis KZ mit dem Zentrum Z ist euklidisch orthogonal zu allen anderen gezeichneten
Kreisen. Z ist das Potenz-Zentrum von KA, KB und KC . Wenn KA, KB und KC die stereografische Bilder
dreier Kugel-Kreise in der vorangehenden Animation wären, würde Z das Bild des Schnittpunkts der
zugehörigen Ebenen a, b und c sein, der Pol bezüglich der Einheit-Kugel von der Ebene ist, deren Schnitt-Kreis
das Bild KZ hat. Die gelb unterlegten Kreise um MBC , MCA und MAB sind die Inversions-Kreise, deren
Spiegelungen KB in KC , KC in KA bzw. KA in KB abbilden. Sie schneiden sich in dem gelben Punkt I1 und
dem nicht sichtbaren Punkt I2 . Diese wären bei der stereografischen Projektion Bilder der Schnitt-Punkte der
Geraden mit der Einheits-Kugel, auf der die Pole der berührenden Kugel-Kreise liegen. Da die Bilder dieser
Pole die Berührkreis-Zentren M1 und M2 sind, liegen I1, I2 , M1 und M2 auf einer Geraden, die auch mit Z
inzidiert. Die dünn gezeichneten Kreise LA, LB und LC durch I1 sind die Lot-Kreise auf KA, KB und KC ,
deren Fuß-Punkte die Berühr-Punkte von K1 und K2 sind. Der Mittelpunkt von zum Beispiel LA ist der
Potenz-Punkt von KA, KZ und dem Null-Kreis um A, also den Kreis um A mit dem Radius Null. Dieser ist
kollinear mit der Geraden durch die Schnittpunkte von KA und KZ , da dies die Potenz-Gerade zu KA und
Z ist.

Das zweite bis achte Bild der Gleitschau zeigt die Stufen der Konstruktion der Berühr-Kreise, wenn zunächst
nur KA, KB und KC in Bild 2 gegeben sind. In Bild 3 sind die äußeren Ähnlichkeits-Zentren zugefügt. Das
Ähnlichkeits-Zentrum MAB zu KA und KB ist zum Beispiel das Zentrum der Streckung, die KA in KB abbildet.
Es teilt die Strecke AB im Verhältnis . MAB ist das stereografische Bild des Pols der Ebene, deren
zugehörige Spiegelung die Ebene a in die Ebene b abbildet, wobei der Pol von a bzw. b das stereografische Bild
A bzw. B hat. Darum ist MAB kollinear mit A und. B . Die Ähnlichkeits-Zentren MAB , MBC und MCA sind
kollinear, da die Hintereinanderschaltung der Streckungen mit den Zentrren MAB und MBC die Streckung
mit dem Zentrum MCA ergibt.

Im vierten Bild wurden die Potenz-Geraden zu Paare je zweier Kreise von KA, KB und KC eingezeichnet.
Sie stehen senkrecht auf der Verbindung-Geraden der Mittelpunkte und der Schnittpunkt teilt zum Beispiel
die Strecke AB im Verhältnis 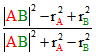. Wenn man KA und KB mit einem beliebigen dritten Kreis
schneidet, dann haben die Geraden durch die beiden Punkte jedes Schnittpunkt-Paars und die Potenz.Gerade
einen gemeinsamen Punkt.

Im fünften Bild ist das Radikal-Zentrum von KA, KB und KC als gemeinsamer Punkt der Potenz-Gerade
schwarz mit magentaferbenen Zentrum markiert und der zugehörige Orthogonal-Kreis KZ schwarz zugefügt.
Seine Schnitt-Punkte mit KA sind die gemeinsamen Punkte von KA mit dem Kreis um den Mittelpunkt der
Strecke AZ durch Z.

Im sechsten Bild sind die Inversions-Kreise eingezeichnet. Ihre Zentren sind die Ähnlichkeits-Zentren und
ihre Radien ergeben sich daraus, dass sie orthogonal zu KZ sind. Die Ebenen der zugehörigen Kugel-Kreise
inzidieren nämlich mit dem Schnittpunkt der Ebenen a, b und c .

Das siebenten Bild zeigt zusätzlich die Verbindungs-Geraden der Schnitt-Punkt von KZ und KA, KB bzw. KC
und ihren Schnitt-Punkt mit der gemeinsamen Geraden der Ähnlichkeits-Zentren. Jeder dieser Schnitt-Punkte
ist Potenz-Punkt zum Tripel der drei Kreise aus KZ, dem Null-Kreis zu einem Schnittpunkt I der Inversions-
Kreise und KA bzw. KB bzw.KC . Das achte Bild zeigt dazu die drei Lot-Kreise durch I, deren Schnitt-Punkte
mit KA, KB und KC die Berühr-Punkte der Kreise K1 und K2 sind, die im neunten Bild zugefügt werden.

Das zehnte Bild zeigt die entsprechende Konstrktion für Berühr-Kreise zu KA, KB bzw. KC , wobei K1 zwei
innen und eines außen berührt und K2 zwei außen und eines innen. Dabei fehlen die Lot-Kreise. Es gibt sie nicht,
weil die Inversions-Kreise keine gemeinsamen Schnitt-Punkte haben. Um zum Beispiel KA in KB zu spiegeln,
reicht nicht die Spiegelung am Kreis um MAB allein, sondern man muss noch die Spiegelung an dem Punkt
MAB nachschalten. Diese Hintereinanderschaltung wird üblicherweise als ' Anti-Inversion am Kreis'
bezeichnet. Diese Variation ist stets bei Kreisen mit inneren Ähnlichkeits-Zentren als Mittelpunkt nötig.

Joseph Gergonne (1771-1859) hat eine Lösung des Kreisproblems von Apollonios gefunden, die sich sich nicht
an der Inkreis-Konstruktion der ebenen Dreiecks-Geometrie orientiert. Sie funktioniert auch für die damit nicht
erfassten Fälle. Zu den drei Kreisen KA, KB und KC gibt es für jedes Paar zwei Ähnlichkeits-Zentren, je ein
äußeres, das wir P-Zentrum nennen, und ein inneres, das wie M-Zentrum nennen. Dabei sind die P-Zentren
kollinear und die Gerade durch zwei M-Zentren inzidiert mit dem P-Zentrum des dritten Kreises. Die vier
Verbindungs-Geraden von Ähnlichkeits-Zentren, die nicht zum gleichen Kreis-Paar gehören, nennen wir
PPP- bzw. PMM- bzw. MPM- bzw. MMP-Gerade. Ausgehend von einer dieser vier Geraden konstruierte
Gergonne die Berühr-Punkte von zwei Kreisen, deren Berührungs-Typ bei KA, KB bzw. KC entgegengesetzt
ist. Zur PMM-Gerade ergibt sich also ein Kreis, der KA außen berührt und KB und KC innen, und ein zweiter
vom entgegengesetzten Berührungs-Typ. Die folgende Gleitschau stellt das Verfahren für eine PPP-Gerade dar,
Es kann unmittelbar auf die andern drei Geraden übertragen werden.

Das erste Bild der Gleitschau zeigt das Ergebnis der Konstruktion mit den wesentlichen Zwischen-Schritten.
Die gelb unterlegte schwarze Gerade ist die PPP-Gerade g mit den äußeren Ähnlichkeits-Zenten von KA,
KB und KC und der schwarze Punkt Z mit dem magentafarbenen Kern das Radikal-Zentrum dieser Kreise.
Die markierten großen farbigen Punkte im Innern von KA, KB und KC sind die Pole von g bezüglich
dieser Kreise. Sie ergeben sich als Schnittpunkt der Polaren zweier beliebiger Punkte von g, Die Berühr-
Punkte von K1 und K2 sind die Schnitt-Punkte der Geraden durch Z und diesen Polen. Das zweite Bild
zeigt die Konstruktion der Pole als ersten Schritt der Gergonne-Verfahrens und das dritte die Zufügung der
Potenz-Geraden zur Ermittlung des Potenz-Zentrums Z.

Das vierte Bild soll zur Begründung der Konstruktion zeigen, dass das Ähnlichkeits-Zentrum von KB und KC
Potenz-Punkt von K1 und K2 ist. Die vier Berührpunkte von KB, KC, K1 und K2 liegen nämlich auf einem
Kreis. Dies erkennt man an der Gleichheit der Produkte und der Sekanten-
Abschnitte. Die Zahlen im fünften Bild zeigen Entsprechendes für die Ähnlichkeits-Zentren von KA und
KB, sowie KC und KA. Darum ist g Potenz-Gerade von K1 und K2.

Das sechste Bild zeigt die Tangenten in den Berühr-Punkten. Die Tangenten in den Berühr-Punkten mit KA
schneiden sich im Potenz-Punkt P von KA, K1 und K2 , der auf der Potenz-Geraden g von K1 und K2 liegt.
Darum muss der Pol von g bezüglich KA auf der Polaren von P bezüglich KA liegen, also auf der Geraden
durch die Berühr-Punkte von KA, K1 und K2 .

Das siebente Bild soll begründen, warum Z auf der Geraden durch die Berühr-Punkte mit KA, KB und KC
liegt. Zu dem Dreieck AM1M2 schneidet die Gerade durch die Berühr-Punkte auf K1 die Seite M2M1 nach
dem Satz von Menelaos (um 100) im Verhältnis . Das gleiche Verhältnis ergibt sich
für KB und KC . Folglich ist Z der Schnitt-Punkt, und Z ist außerdem Ähnlichkeits-Zentrum von K1 und K2.

Die letzten drei Bilder zeigen die Ergebnisse der Gergonne-Konstruktion für die PMM-, MPM- und MMP-Gerade.



::::