Es lebe die Geometrie!

Das Analogon des Höhenfußpunkt-Dreiecks beim 6-Rechteck

Wie auf den drei vorherigen Seiten gehen wir in den folgenden Animationen von einem 6-Rechteck
ABCDEF aus, bei dem wir die Kanten AB, CD und EF den Eckpunkte des Analogie-Dreiecks im Bild
unten rechts zuordnen und die Kanten BC, DE und FA den Dreiecks-Seiten. Der Fokus liegt dabei auf
dem 6-Rechteck A'B'C'D'E'F', das dem Dreieck der Höhenfußpunkte entspricht. Das Analogie-Dreieck
ist hier das Dreieck der Ankreis-Mittelpunkte zum Dreieck der Höhenfußpunkte. Darum steht ABCDEF
hier im gleichen Verhältnis zu A'B'C'D'E'F' wie auf der vorangehenden Seite zu den Winkelhalbierenden
das 6-Rechteck A*B*C*D*E*F* zu ABCDEF . Die Kanten von A'B'C'D'E'F' werden mit den gleichen
Farben wie bei ABCDEF gezeichnet, aber zusätzlich durch einen weißen Mittelstreifen markiert. Genauso
gehen wir beim Analogie-Dreieck vor. Anders als bei ABCDEF entsprechen bei A'B'C'D'E'F' die in dunkler
Farbe gezeichneten Kanten nicht den Kanten des analogen Dreiecks der Höhen-Fußpunkte unten rechts,
sondern den Eckpunkten dieses Dreiecks.

Wir gingen bei dieser Zeichnung von dem 6-Rechteck ABCDEF mit den Höhenloten und der Höhen-
Achse aus, das schon auf der Seite 6-Rechteck 1 dargestellt wurde. Hinzugefügt wurde die mit weißer
Mittel-Linie markierte Strecke B'C' bzw. D'E' bzw. F 'A' , die dem grünen bzw. roten bzw. blauen
Höhenfußpunkt im Analogie-Dreieck entspricht. Die Gerade zu dieser Strecke schneidet die Kante BC
bzw. DE bzw. FA im Fußpunkt P ihres gemeinsamen Lots mit der violett gezeichneten Höhen-Achse und
ist orthogonal zur Kante und dem Lot. A'B'C'D'E'F ' ist dann das 6-Rechteck, das sich aus den Fußpunkten
der gemeinsamen Lote dieser drei Geraden ergibt. Bemerkenswert ist dabei, dass P dann in der durch ein
Kreuz markierten Mitte der Kante B'C' bzw. D'E' bzw. F 'A' liegt. Dem entspricht im Analogie-Dreieck,
dass jede Höhe Winkelhalbierende im Dreieck der Höhenfußpunkte ist.

Bei A'B'C'D'E'F ' führt diese Analogie nicht nur zu einer Gleichheit bei den Streckenlängen, sondern auch
bei den Winkelgrößen. Dazu betrachten wir die dunkelblaue Strecke F 'A' mit dem weißen Mittelstreifen, die
an die hellgrüne Kante E'F ' anschließt und auf welche die hellrote Strecke A'B' folgt. Das hellblaue gemeinsame
Lot g der Strecken FA und CD steht dann im Mittelpunkt von F 'A' senkrecht auf FA und F 'A'. Ein Richtungs-
Vektor dieses Lots g bildet mit dem Richtungs-Vektor von E'F ' einen gleich großen Winkel 62° wie mit dem
Richtungs-Vektor von A'B' . Dennoch ist die Kanten-Gerade zu FA nicht Mittelsenkrechte von F 'A'. Denn
ein Tripel-Paar von g ergibt sich hier nicht als normierte Differenz der Tripel-Paaren zu E'F '' und A'B', sondern
als deren normierte Summe. Dies soll das Mitten-Kreuz in der Zeichnung dadurch ausdrücken, dass nicht die
graue Strecke des Kreuzes auf FA liegt, sondern die schwarze. Dabei haben wir vorausgesetzt, dass die
Richtungs-Vektoren von A'B'C'D'E'F ' wie bei einem Umlauf um das 6-Eck koordiniert sind.

Anders als in der vorherigen Animation hat hier ABCDEF nicht nur Kanten der Länge 1. Die
vorangehende Konstruktion wurde durch die Raumgeraden ergänzt, die in dem Analogie-
Dreieck den Loten von den Eckpunkten des Ausgangs-Dreiecks auf die nächstgelegenen Seiten
der Dreiecks aus den Höhen-Fußpunkten entsprechen. Diese schneiden sich dort in dem Umkreis-
Mittelpunkt O. Die Existenz eines gemeinsamen Schnittpunkt entspricht bei den Raumgeraden der
Existenz eines gemeinsamen Lots. Dieses Lot entspricht aber nicht dem Umkreis-Mittelpunkt. Das
zeigen die letzten drei Bilder der Gleitschau, in denen die magentafarbene Mittelsenkrechten-Achse
zugefügt wurde. Jedoch eine andere Eigenschaft von O hat eine Entsprechung bei den Raumgeraden.

O ist nämlich der zum Höhen-Schnittpunkt H isogonal konjugierte Punkt. Das bedeutet, dass in jedem
Eckpunkt die beiden markierten Winkel zwischen einer Dreiecks-Seite und einer Höhe bzw. einem Lot
auf eine Seite des Höhenfußpunkt-Dreiecks gleich groß sind. Dieser Winkel-Gleichheit entspricht bei
ABCDEF einer Übereinstimmung bei Strecken-Längen und Winkel-Größen. Dazu betrachten wir die
hellgrüne Kante EF. Von EF gehen zwei Lote g und h aus, deren Fußpunkten symmetrisch zum Mittelpunkt
von EF liegen. g ist gemeinsames Lot der Kanten-Geraden von EF und der violetten Höhen-Achse, die H
entspricht. h ist gemeinsames Lot mit der violett-weißen Achse, die O entspricht. Ein schwarzer
Mittel-Streifen unterscheidet h von g. Von DE hat g den Abstand 0,47 und sein Richtungsvektor schließt
mit dem von DE einen Winkel von 97° ein. Für h gelten die gleichen Maße bezogen auf FA. Das
erweiterte innere Produkt für g und DE bzw. h und EF , das auf der Seite ' 6-Rechteck 1' erklärt wurde,
hat in beiden Fällen das gerundete Werte-Paar , das man auch als duale
Zahl schreibt.

Wir nennen Raumgeraden p und q, die zu einem 6-Rechteck in einem entsprechenden Verhältnis stehen
wie isogonal konjugierte Punkte P und Q in dem Analogie-Dreieck, ebenfalls 'isogonal konjugiert'. Den
Kanten-Geraden BC, DE und FA des 6-Rechtecks seien nicht (notwendig d-normierte) Dualzahl-Tripel
s, u und w zugeordnet, wie es auf der Seite ' 6-Rechteck 1' erklärt wurde. p bzw. q sei Dualzahl-Tripel
der isogonal kongugierten Raum-Geraden p bzw. q. Dann berechnet man q nach der Formel
.
p braucht hierbei ebenfalls nicht d-normiert sein. Für q wird dies im Allgemeinen auch nicht gelten, da Real- und
Dual-Teil von q das Tripel-Paar keiner Geraden, sondern eines Gewindes bilden. Siehe die Erklärung am Schluss
der Seite ' 6-Rechteck 1'. Wenn p Höhen-Achse ist, ergibt sich für die O entsprechende violett-weißen Achse das
Dualzahl-Tripel .

Wenn s, u und w in normierter Form vorliegen, gilt

In der vorhergehenden Animation wurde im Analogie-Dreieck unten rechts von jedem Eckpunkt des
Dreiecks nur das Lot auf die nächstgelegene Seitengerade des Dreiecks der Höhen-Fußpunkte gefällt.
In dieser Animation kommen jeweils die andern beiden Lote hinzu. Sie ergeben sich aus dem ersten Lot
durch Spiegelung an den Seiten des Ausgangs-Dreiecks. Die Lotfußpunkte liegen dann symmetrisch zu den
Höhen-Fußpunkten auf den Seitengeraden des Dreiecks der Höhen-Fußpunkte.

In der entsprechenden Figur der Raumgeraden wird aus jeder Gleichheit von Strecken-Längen oder Winkel-
Größen im Analogie-Dreieck eine Gleichheit von zwei Paaren, bestehend aus einer Strecken-Länge und einer
Winkel-Größe, die man wie oben erklärt zu einer Dual-Zahl zusammenfassen kann. Aus der zweidimensionalen
Spiegelung an einer Seiten-Gerade wird eine dreidimensionaleSpiegelung an einer entsprechenden Gerade des
6-Rechtecks.

Die Animation zeigt die Konstruktion der cyanfarbenen Strecke, deren Raumgerade dem
Symmedian-Punkt Y in dem Analogie-Dreieck unten rechts entspricht. Y liegt auf jeder der
drei mit einem schwarzen Mittelstreifen markierten Geraden, die einen Eckpunkt dieses Dreiecks
mit der Mitte der nächstgelegenen Seite im Dreieck der Höhen-Fußpunkte verbindet.


Den Kanten-Geraden BC, DE und FA des 6-Rechtecks seien d-normierte Dualzahl-Tripel s, u und
w zugeordnet. Die Determinante der Matrix mit diesen Tripeln als Zeilen ist dann .
Mit der Graßmann-Identität berechnet man so eine Raumgerade, die einem Höhenfußpunkt entspricht:

Um aus m ein d-normiertes Tripel zu erhalten, teilen wir m durch .
Die den anderen Höhenfußpunkten entsprechenden Geraden ergeben sich durch zyklisches Permutieren
der Tripel s, u, w . Zur Berechnung eines Tripels, das einem Mittelpunkt im Höhenfußpunkt-Dreieck
entspricht, hat man zwei Möglichkeiten, nämlich die Addition oder die Subtraktion der Tripel, die zwei
Höhenfußpunkten zugeordnet sind, z.B. : . Das Kreuz-Produkt von zwei
derartigen Tripeln ergibt das Tripel einer Raumgeraden, die dem Symmedian-Punkt entspricht, nämlich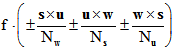
, wobei f eine Dual-Zahl ist, die durch Kürzen verschwindet, wenn man
dieses Tripel normiert. Hier entsprechen also vier Raumgeraden dem Symmedian-Punkt im Analog-Dreieck.