Es lebe die Geometrie!

Die Astroide

Der dick gezeichnete Rastkreis hat im Folgenden stets den Radius 1.

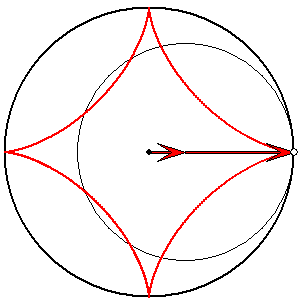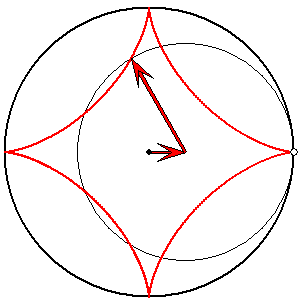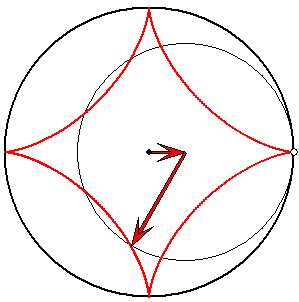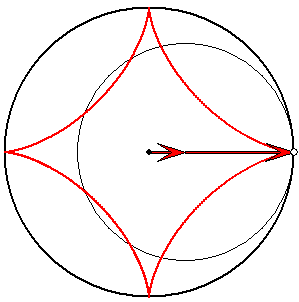
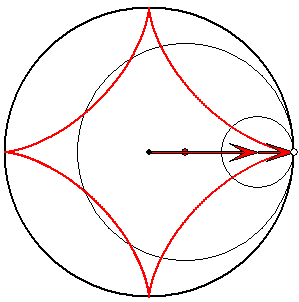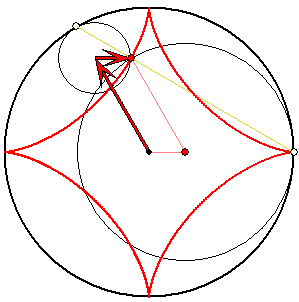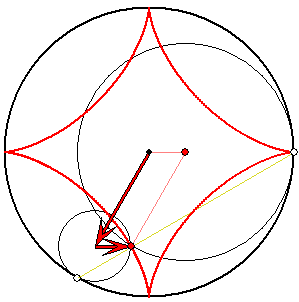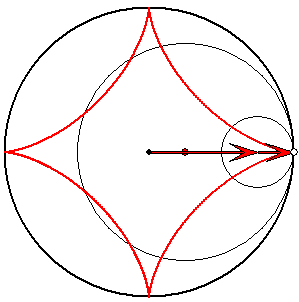
Spur vom 1/4-Gangkreis
Die Astroide ist die Spur eines Punktes auf
dem Rand eines Gangkreises mit dem Radius
3/4, der am Rastkreis ohne zu Rutschen abrollt.

Spur beider Gangkreise
Die Astroide entsteht auch dadurch, dass
ein Gangkreis mit dem Radius 1/4 abrollt.
Die Berührpunkte der beiden Gangkreise
und der Spurpunkt sind kollinear.

Die Winkelgeschwindigkeiten des langen zum kurzen roten Pfeil verhalten sich wie 1 zu -3. Wenn
bzw. der Richtungswinkel des kurzen bzw. langen Pfeils ist, dann gilt und für den
Richtungswinkel des Spurpunkts der Zykloide .

Astroide und {-4;+4}-Zykloide
Neben der roten Astroide wird hier die zugehörige dunkelgrüne {-4;+4}-Zykloide zusammen mit deren
hellgrünen Bogenmitten-Evolvente und der schwarzen Spitzen-Evolvente dargestellt. Die roten Pfeile haben
die Längen 1/4 und 3/4, die dunkelgrünen die Längen 3/8 und 5/8 und die hellgrünen die Längen 3/32 und
5/32. Die Spitze des weiß gefüllten Pfeils mit der Länge 15/16 zeichnet die Spur der Spitzen-Evolvente der
{-4;+4}-Zykloide. Diese Evolvente kann sowohl in einem regulären Dreieck, als auch in einem regulären
Fünfeck so gedreht werden, dass alle Seiten berührt werden, ist also sowohl ein Triphil als auch ein
Pentaphil.

Die Gerade durch den langen roten Pfeil ist Tangente der {-4;+4}-Zykloide, ebenso die Kathete des blauen
Dreiecks durch die Spitze. Die Berührpunkte sind die Spitzen der langen Pfeile. Der Katheten-Schnittpunkt
des blauen Dreiecks ist der Gegenpunkt vom Berührpunktes des 3/4-Gangkreises. Der Schnittpunkt der
Hypotenuse mit der Geraden durch den kurzen dunkelgrünen Pfeil liegt auf dem Rastkreis der hellgrünen
Bogenmitten-Evolvente.

Teilverhältnisse
Zu der Astroide (-4-Zykloide) ist hier die +4-Zykloide hinzugezeichnet, die dadurch entsteht, dass
ein 1/4-Gangkreis außen am Rastkreis abrollt. Die blaue Verbindungsgerade der beiden roten Punkte
P und Q auf diesen Zykloiden berührt die grüne {-4;+4}-Zykloide in der Spitze des kurzen grünen
Pfeils. Die blaue Orthogonale in diesem Punkt geht durch die Rastkreis-Berührpunkte des 3/4- und
des 5/4-Gangkreises. Die Spitze des weißen Pfeils auf der Spitzen-Evolvente der {-4;+4}-Zykloide
teilt die Strecke PQ im Verhältnis 5 : 3. Im gleichen Verhältnis teilt der dunkelgrüne Punkt diese
Strecke außen.

Tangenten-n-Ecke
Die Spitzen-Evolvente der {-4;+4}-Zykloide ist sowohl ein Triphil, als auch ein Pentaphil. Die
Tangenten-Vielecke, bei denen jeder Innenwinkel zwischen aufeinanderfolgenden Seiten die Größe
180°-360°/n hat, haben für alle Eckenzahlen n mit Ausnahme von n = 4 die gleiche Umfangslänge.