Es lebe die Geometrie!

Steiner-Gleichdick

-->Figuren mit konstanter Breite
https://www.vivat-geo.de/Pdf-Dateien/Gleichdick.pdf

Eine Menge heißt konvex, wenn sie mit zwei Punkten stets die ganze Verbindungsstrecke
enthält. Ein Gleichdick ist eine konvexe Menge, bei der jede Tangente von der dazu parallelen
Tangente auf der anderen Seite der konvexen Menge den gleichen Abstand hat. Der
Abstand wird als Breite bezeichnet. Gleichdicke werden darum auch als 'Figuren mit
konstanter Breite' bezeichnet. Leonhard Euler (1707-1783) benutzte den Begriff 'Orbiform'.

Der Pfeil dreht sich stets um den gelben Punkt, dessen Lage auf dem Pfeil durch die Drehpunktfunktion
f(a) = sin(3a) festgelegt wird. Dabei ist a der Richtungswinkel des Pfeils, also der Winkel zwischen
dem Pfeil und der Rechtsachse. f(a) gibt die Lage des gelben Punktes in einem eindimensionalen
Koordinatensystem auf dem Pfeil an, bei dem die Pfeilspitze die Koordinate 1, die Mitte die Koordinate 0
und das Pfeilende die Koordinate -1 hat. Die rot gezeichnete Ortskurve der Pfeilspitze ist der Rand eines
Gleichdicks. Die dunkelblau gezeichnete Ortskurve des Drehpunkts ist hier eine Steiner-Zykloide.

Mit Hilfe eines Riemann-Integrals wird die Steiner-Zykloide in komplexer Schreibweise durch die Funktion
dargestellt. g sei die Drehpunktfunktion der roten Kurve mit dem
Startpunkt bei 1 in der komplexen Ebene. Wenn der Richtungswinkel des Pfeils um einen sehr kleinen
Winkel von auf wächst, rückt die Pfeilspitze in Richtung um ein Wegstück
weiter, das ungefähr den Betrag hat. Dabei strebt für auch der Fehler gegen
Null. Darum wird das Gleichdick durch die Kurvenfunktion
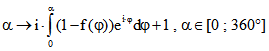beschieben.
(Siehe http://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf).
Die rote Kurve ist die Evolvente der dunkelblauer Kurve durch deren Spitzen. Die hellblaue Kurve ist die
Evolvente durch die Bogenmitten der Steiner-Zykloide. Sie ist die Spur des Nullpunkts vom bewegten Pfeil.
Ihre Funktions-Darstellung ergibt sich, indem man in der Funktion der Spitzen-Evolvente die 1 durch 0 ersetzt.

In der Gleitschau im Anschluss an die Animation sind acht Standbilder daraus angegeben. Danach folgen
achtzehn Bilder mit umschließenden Tangenten-Quadraten. Deren Mitte M liegt auf dem Inkreis der
Bogenmitten-Evolvente. Die Verbindungsstrecken gegenüberliegender Tangenten-Berührpunkte des
Gleichdicks schneiden sich rechtwinklig in einem Punkt Q des Inkreises der blauen Drehpunktkurve und
berühren die Steiner-Zykloide in den Drehpunkten R und S. Dabei ist R der Drehpunkt des Pfeils. R, Q
und S spannen ein Rechteck mit dem vierten Eckpunkt T auf. Dabei teilt M die Diagonale QT im Verhältnis
2 : 1. Die zweite Diagonale RS berührt die Steinerzykloide im Fußpunkt des Lots von T auf RS. Die
Eckpunkte des Tangenten-Quadrats liegen auf einer Kurve, die man als Bahnkurve einer Überlagerung
von zwei gleichförmigen Kreisbewegungen beschreiben kann, wobei die eine Winkelgeschwindigkeit
viermal so groß ist wie die andere.

Hier wird für Richtungswinkel im Abstand von 2,5° die Verbindungsstrecke gegenüberliegender
Berührpunkte des Tangenten-Quadrats hellblau eingezeichnet. Sie haben bei der Drehpunktfunktion
f(a) = sin(3a) die Besonderheit, dass sich jeweils drei von ihnen in einem Punkt schneiden, nämlich
wenn die Summe der zugehörigen Richtungswinkel 180° oder 360° beträgt.

Anders als in den vorherigen Animationen wird das Steiner-Gleichdick hier nicht mit einer Evolvente
der Steiner-Zykloide erzeugt, sondern als Drehpunkt-Kurve, deren Evolute die Steiner-Zykloide ist.
Die zugehörige Drehpunktfunktion entsteht hier in der ersten Periode der
Animation aus einer Stammfunktion von durch Ersetzung von durch . Es
ergibt sich das Gleichdick in der gleichen Größe und Orientierung wie in den vorigen Animationen, aber
mit einem anderen Startpunkt. Die Evolute hat die Ableitung von als
Drehpunktfunktion. Der Graph dieser Ableitung geht durch Verschiebung aus dem Graphen von
hervor.

In der zweiten Periode der Animation wurde die Drehpunktfunktion benutzt.
Die Änderung des Vorzeichens im Funktionsterm bewirkt einen Graphen, der aus dem der ersten Periode
durch eine Punkt-Spiegelung entsteht.

Die dunkelgrüne Kurve entsteht durch Punktspiegelung der rote Ortslinie. Die hellgrünen ergeben
sich durch Verschiebung dieser Kurve in die jeweils aktuelle Pfeilspitze. Wenn die rote Ortslinie
ein Gleichdick berandet, überdecken die hellgrünen Kurve stets eine Kreisfläche. Die Vektormenge
dieser Kreisfläche ergibt sich, indem man die Ortsvektoren der Punkte des Gleichdicks mit den
Ortsvektoren der Punkte des Spiegelungsbildes addiert (Minkowski-Addition).

Das vierte Standbild in der Gleitschau nach der Animation zeigt die Drehpunktkurven zu den
Drehpunktfunktionen und , aus
denen durch Adition die Drehpunktfunktion des Kreises entsteht.

In dieser Animation werden zu der Steiner-Zykloide nicht nur die Evolventen durch die Spitzen und
die Bogenmitten betrachtet, sondern auch alle dazwischen liegende Evolventen. Sie werden in der
komplexen Ebene durch die Funktion 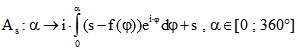beschrieben
mit einem s-Wert zwischen 1 und 0. Wir nennen die Evolvente zu s die 's-Kurve' der Steiner-Zykloide.
Das von den Tangenten in den Punkten , , und
gebildete Rechteck ist ein Quadrat mit der Seitenlänge 2s, also unabhängig vom Richtungswinkel.
Die Mitte des Quadrats liegt stets auf dem Inkreis der Evolvente durch die Bogenmitten, also der
Null-Kurve.