Es lebe die Geometrie!

Das Hyperbel-Modell
der hyperbolischen Geometrie

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Die Animation zeigt eine Schale des Hyperboloids . Ihr Scheitelpunkt (0 ; 0 ; 1)
ist das Zentrum eines Einheitskreises in der Ebene z = 1, mit einem Dreieck ABC im Klein-Modell
zu diesem Kreis. Die Ursprungsgerade durch A bzw. B bzw. C schneidet die Hyperboloid-Schale
in A' bzw. B' bzw. C'. Diese Punkte werden parallel zur z-Achse auf die Punkte A'' , B'' und C''
in der x-y-Ebene projiziert. Die Ursprungsebene durch B und C schneidet die Hyperboloid-Schale
in einem Hyperbel-Ast, und die Projektion auf die x-y-Ebene ergibt ebenfalls einen Hyperbel-Ast.
Das Gleiche gilt für die Ursprungsebenen durch C, A und A, B.

Ohne den Umweg über das Hyperboloid erhält man die Hyperbel-Äste in der x-y-Ebene aus einem
Klein-Modell, das mit dem Zentrum im Ursprung Z in der x-y-Ebene plaziert wird, mit Hilfe der
Abbildung 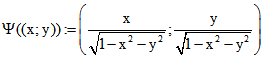der Punktmenge dieses Klein-Modells auf
die Punktmenge der x-y-Ebene. Wenn A° das Bild von A bei der Projektion parallel zur z-Achse
in die x-y-Ebene ist, dann ist . Entsprechendes gilt für B und C . Durch werden
die Strecken des Klein-Modells auf Ursprungsgeraden oder Hyperbel-Äste abgebildet, deren
Asymptoten sich im Ursprung Z schneiden und bei denen die Länge des Nebenachsen-Abschnitts
gleich 1 ist. Jeder Hyperbel-Ast ist eine Kurve mit der Gleichung ,
wobei p und q Zahlen mit sind. (p ; q) ist das kartesische Koordinatenpaar des Pols
der Sehne des Klein-Modells, deren Bild bei der Hyperbel-Ast ist. Dieser Pol kann auch als Pol
des Hyperbel-Astes bezeichnet werden.

Diese Hyperbel-Äste und die Ursprungsgeraden sind die 'Geraden' des Hyperbel-Modells, hier auch
Y-Geraden genannt. Die Y-Punktmenge ist die Menge aller Punkte der x-y-Ebene. Das Winkel-Maß
und das Abstands-Maß des Modells ergibt sich durch eine Übertragung aus dem Klein-Modell. Die
Größe des Winkels zwischen zwei Hyperbel-Ästen g und h ist die euklidische Größe des Winkels
zwischen den Kreisen um ihre Pole, welche ihre Asymptoten berühren. Der signierte Abstand eines
Punktes Q auf g vom Scheitelpunkt S von g ist , wobei und
die Asymptoten von g sind.

Die Abbildung unten zeigt ein Dreiseit im Hyperbel-Modell mit Y-Seitenhalbierenden, Y-Mittelsenkrechten,
Y-Höhen und Y-Winkelhalbierenden. Wie im Klein-Modell haben die Y-Mittelsenkrechten und
Y-Höhen nicht notwendig einen Schnittpunkt. Wenn sich aber zwei dieser gleichartigen Y-Geraden
schneiden, dann geht auch die dritte durch diesen Schnittpunkt.