Es lebe die Geometrie!

Reguläre Fourier-Polygone ohne negative Seitenlängen

Die folgenden Seiten über Fourier-Polygone behandeln Drehpunktkurven zu Fourier-Reihen in der
Form
oder
für ganze Zahlen n, m, und p mit n > 1, m >= 0 und p >= 1, wobei weder p - m noch p + m gleich
einem Produkt mit einer ganzen Zahl k sei. Insbesondere darf also p nicht gleich m sein. Im Fall
m = 0 tritt beim Summand zu k = 0 der Nenner Null auf. Dann denken wir uns diesen Summanden im
Sinus-Fall durch den Term ersetzt und im Kosinus-Fall durch Null. Die so definierten Funktionsterme
kürzen wir mit bzw. ab. Wenn wir Teilsummen dieser
unendlichen Summen betrachten, ersetzen wir hierbei die Grenzen und durch die zugehörigen Ober-
und Untergrenzen von k.

Wir nennen eine Drehpunktkurve 'p-geschlossen', wenn
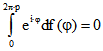ist. Für ist 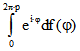gleich Null genau dann, wenn
ist. Darum darf für keine ganze Zahl k das Produkt gleich oder
sein, wenn mit FS ein (geschlossenes) Polygon erzeugt werden soll. Entsprechendes gilt für FC.

Die Drehpunktkurven zu FS und FC sind Polygone, weil diese Funktionen treppenförmig sind. Die
Sprungstellen, an denen sich die Stufenhöhe ändert, sind die ganzzahligen Vielfachen des Richtungswinkels
. An diesen Stellen haben die Funktionen FS und FC als Funktionswert den Mittelwert der Höhen von
den links und rechts anschließenden Stufen. Die Stufenhöhen stimmen mit denen der folgenden
Treppen-Funktionen überein:

Für m = 0 :
bzw. (im Kosinus-Fall)
und sonst:
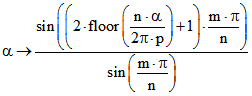bzw.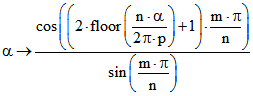
Wenn m halb so groß wie n ist, sind dies die Funktionen bzw. .

Das Polygon, das durch die Drehpunktkurve zur Drehpunktfunktion
bzw.
dargestellt wird bezeichnen wir mit bzw. .

Auf dieser Seite betrachten wir den Fall m = 0, auf der folgenden Seite den Fall 2m = n und auf der
übernächsten den allgemeinen Fall ' m ungleich Null '.

Die Animation zeigt die blauen Drehpunktkurven zusammen mit ihren orangefarbigen Evoluten
(also dem geometrischen Ort der Krümmungsmittelpunkte) von fünf Teilsummen von
, nämlich den Teilsummen
,
,


und .
In der ersten Periode ergibt sich ein Kreis mit dem Radius und in der zweiten die Evolvente einer
Astroiden durch zwei ihrer Spitzen. In den folgenden Perioden nähert sich die Drehpunktfunktion
immer mehr der Treppenfunktion an und die Drehpunktkurve einem Zweieck
mit der Seitenlänge 2. Diese Seitenlänge ist die Sprunghöhe der Treppenfunktion.

In der Gleitschau werden auf die Animation folgend Standbilder daraus gezeigt.

Hier werden Näherungsfunktionen von mit ihren Drehpunktkurven
dargestellt. Es sind die Funktionen
,
,
,
und
.
Die Drehpunktkurven sind ein Kreis mit dem Radius , die Spitzen-Evolvente einer Steiner-Zykloide
und Näherungskurven eines gleichseitigen Dreiecks mit der Seitenlänge 2. Die Umfanglänge des Dreoecks
stimmt mit der des Ausgangskreises überein.

Die Animation zeigt folgende Näherungskurven zur Drehpunktfunktion
,
,

,
und


Der Richtungspfeil der Kurven macht beim Erzeugen der Kurven zwei volle Umdrehungen. Die
Kurve nach dem Kreis ist ein Triphil. Drei Tangenten zu Richtungswinkeln , und
bilden also für alle kongruente Dreiecke. Das Fourier-Polygon zu
ist ein Pentagramm mit der Seitenlänge 2, dessen Umfangslänge also mit dem des Ausgangskreises
übereinstimmt..

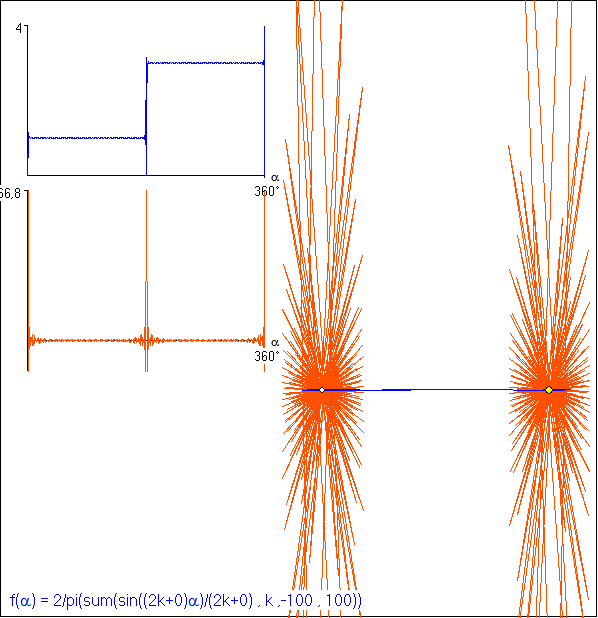
Die ersten vier Näherungskurven von Polygonen in der Gleitschau gehören zu der Funktion
für n = 2, 3 , 4 und 5. Die Drehpunktkurven zu den Funktionen
sind die Polygone mit den eingezeichneten weiß gefüllten Punkten.
Sie sind regulär und haben die Überschlagungszahl 1. Es folgen 5-Ecke PS(5;0;p), 6-Ecke
PS(6;0;p) und 7-Ecke PS(6;0;p) mit p gleich 2, 3 oder 4. Die Zahl p, wlche die Anzahl der vollen
Umdrehungen angibt, die der Richtungspfeil der Kurve bei der Konstruktion durchlaufen muss,
stimmt hier (für m = 0) mit der Überschlagungszahl des Polygons überein. Alle Polygone haben die
Seitenlänge 2 und darum die gleiche Umfangslänge wie der Startkreis der Fourier-Approximation..

Im Bild zu n = 2 zeigt sich deutlich ein Phänomen, dass nach dem Physiker und Mathematiker
Josiah Gibbs (1839-1903) benannt ist. Obwohl für die Zeichnung sehr viele Summanden (nämlich
201) berücksichtigt wurden, ist die gezeichnete Drehpunktkurve deutlich länger als die Strecke
zwischen den Eckpunkten. Endsprechend gibt es bei der Drehpunktfunktion an der Sprungstelle
Werte, die über die folgernde Stufenhöhe hinausgehen. Die Abweichung dieser überschießenden
Werte gegenüber der Stufenhöhe konvergiert nicht gegen Null, wenn die Summandenzahl gegen
Unendlich geht. Das ist insofern bemerkenswert, als die Fourier-Reihe für alle
konvergiert, so dass gilt: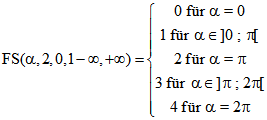

Die Fourier-Reihe konvergiert sogar gleichmäßig in jedem abgeschlossenen Intervall, das keine Sprungstelle
enthält. Dies bedeutet, dass mit wachsender Anzahl von Summanden die überschießenden Werte zwar nicht
verschwinden, aber sich auf einen immer kleineren Bereich links und rechts von der Sprungstelle beschränken.