Es lebe die Geometrie!

Flächeninhalte und Bogenlängen bei Evolventen von {-k;+k}-Zykloiden

Zur Berechnung von Flächeninhalten und Bogenlängen ist die Drehpunktfunktion besonders geeignet.
Dies soll hier für die Evolventen der [-k;+k}-Zykloiden gezeigt werden. Eine dazu passende Drehpunkt=
funktion ist . Denn die zugehörige Drehpunkt-Kurve ist der Graph der
Funktion .

Die Benutzung der Drehpunktfunktion für die Berechnung von Flächeninhalten und Bogenlängen beruht
auf den Termen und , welche diese Aufgabe für einen Kreis-Sektor zum Radius r
und zum Mittelpunktswinkel löst. Unter stellt man sich den Winkel zwischen zwei benachbarten
Tangenten der Drehpunkt-Kurve vor und unter r den signierten Abstand eines Drehpunkts D von einem
Punkt P, der hier eine Evolvente als Spur hat. Die berechnete Fläche ist dann die Menge der Punkte, die
von der Strecke DP überstrichen wird, wenn man die eine Tangente in die andere bewegt. Dabei macht man
zunächst einen Fehler, da diese Fläche im Allgemeinen kein Kreis-Sektor ist. Der Fehler verschwindet aber
für . Darum ist der Inhalt einer von der Strecke DP
überstrichenen Fläche, wobei die Konstante a die Evolvente charakterisiert. Diese Berechnung ist allerdings
nur dann korrekt, wenn DP keinen Punkt mehrfach überstreicht. Analog betrachten wir das Integeral
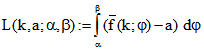. Unter der Voraussetzung gibt der Integralwert die Länge
des von P als Spur gezeichneten Wegstücks an. Wenn die Voraussetzung nicht erfüllt ist, ist der Integralwert
eine Differenz von Längen derartiger Wegstücke, also möglicherweise negativ. Wir bezeichnen den Wert des
Integrals als 'signierte Bogenlänge' zwischen den beiden Richtungswinkeln der Integrationsgrenzen.

Wegen ist stets
.
Der Inhalt der Fläche zur a-Evolvente ergibt sich also aus dem für die Null-Evolvente, indem man das a-fache
der signierten Bogenlänge der Null-Evolvente abzieht und den Inhalt eines Kreis-Sektors zum Radius und
zum Mittelpunktswinkel addiert.

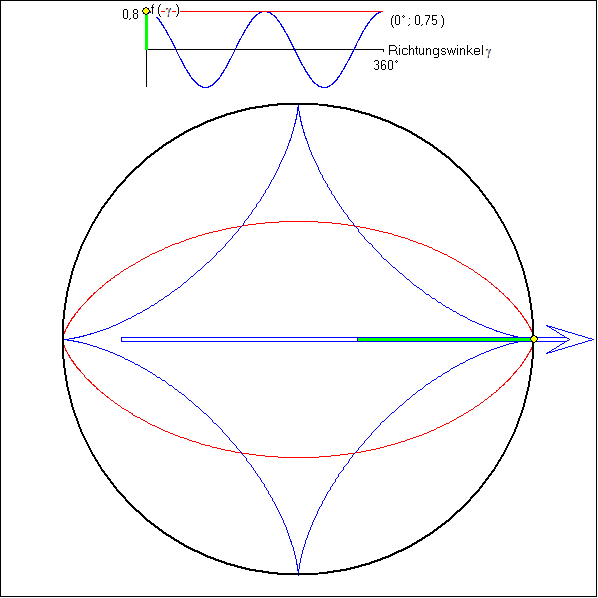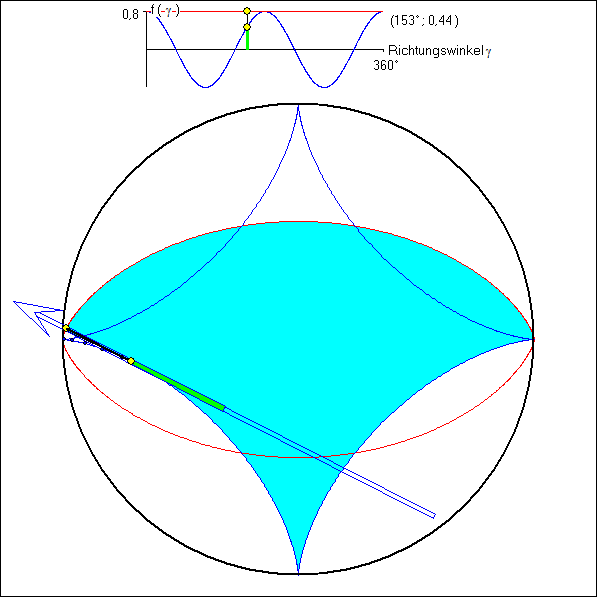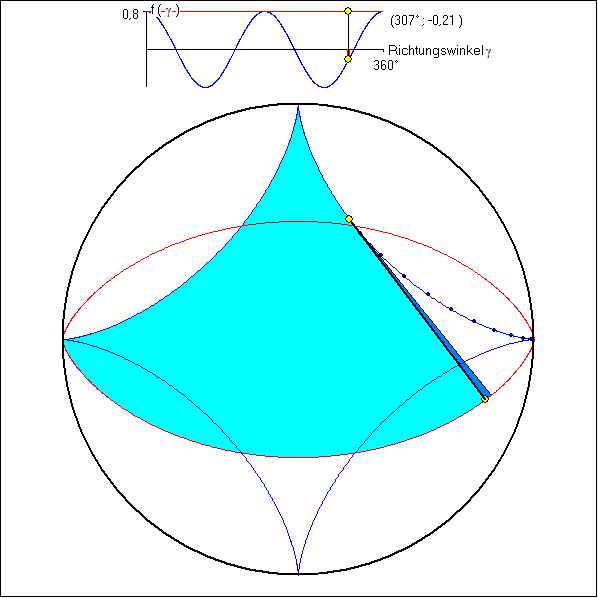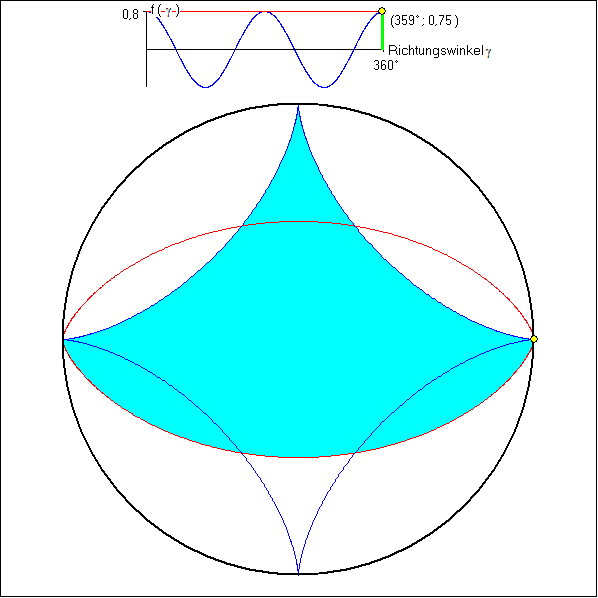
Hier wird die Drehpunktfunktion für die [-2;+2}-Zykloide (Astroide) benutzt.
Die rote Kurve ist die 0,75-Kurve (Spitzen-Evolvente) dazu. Sie ist ein Triphil. Die hellblaue Fläche hat in
ihrer maximalen Fassung den Flächeninhalt .
Sie setzt sich aus je einer halben Triphil-Fläche und einer halben Astroiden-Fläche zusammen. Da die Astroide
als -4-Zykloide den Flächeninhalt hat, beträgt der Flächeninhalt des Triphils
.
Die (unsignierte) Bogenlänge des Triphils ist .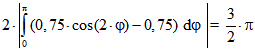

Die rot-grün gezeichnete Kurve ist die a-Kurve zur Drehpunktfunktion für
a = 0 und a = 0,25. Für a = 0 ergibt sich die Bogenmitten-Evolvente der blauen Astroide, die selbst
eine Astroide ist. Man errechnet . Dies ist für a = 0 und a = 0,25
die hellblaue Fläche in ihrer größten Ausdehnung. Für a > 0,25 ist die Formel zur Flächenberechnung
weniger geeignet, weil es bei der überstrichenen Fläche zu Überlappungen kommt. Da im Fall a = 0 die
ausgesparte Astroiden-Fläche 1/4 der Fläche von der blauen Astroide ausmacht, hat diese den Inhalt
.
Für den Bogenlängen-Term errechnet man . Dies ergibt Null für a = 0,
weil die rot-grüne Astroide aus vier gleich langen Bögen zusammengesetzt ist, die bei der Berechnung
der signierten Bogenlänge je nach der Farbe rot/grün mit dem Vorzeichen - oder + eingehen. Jeder
dieser Bögen hat die Länge . Bei a = 0,25 ist die signierte Bogenlänge
negativ, weil die roten Bögen länger sind als die grünen. Für den Richtungswinkel einer
Tangente der blauen Astroide in einer Spitze der rot-grünen gilt mit der Lösung
falls . Mit diesen Winkel ergibt die (unsignierte) Umfangslänge der
rot-grünen 0,25-Kurve
.