Es lebe die Geometrie!

Geodäten

--> https://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf

Die magentafarbene Kurve auf der Pseudosphäre stellt eine Geodäte dar. Der schwach gezeichnete Schatten
auf der x-y-Ebene ergibt sich durch Projektion parallel zur z-Achse. Die Abbildungen oben rechts und
links zeigen die Bilder diese Geodäte, wenn man die Pseudosphäre auf die nach Henri Poincare (1854-1912)
bzw. Felix Klein (1849-1925) benannten Modelle der hyperbolischen Geometrie abbildet. Die Bilder sind
Kreisbögen bzw. Strecken. Das nach Klein benannte Modell wird auch Beltrami-Klein-Modell genannt, weil
es schon in Ideen von Eugenio Beltrami (1835-1900) angelegt war.

Wenn die Pseudosphäre in Zylinderkoordinaten (r;w;z) durch z = f(r) gegeben ist, dann beschreibt
die Abbildung der Pseudosphäre auf das in kartesischen Koordinaten gegebene
Poincare-Modell, wobei die Winkelgröße w im Bogenmaß auf der Rechtsachse aufgetragen ist. Wenn
auch die Pseudosphäre in kartesischen Koordinaten beschrieben wird , lautet die Abbildungsvorschrift . Die Abbildung von der Pseudosphäre in das Beltrami-Klein-Modell
wird durch 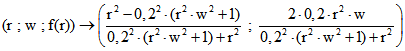beschrieben.

Die Bildmenge für ist im Poincare-Modell die Menge der Punkte oberhalb der gelb-grauen
Parallelen g zur Rechtsachse durch den Punkt (0 ; 1), die zwischen den gelb-grau gezeichneten Parallelen zur
Hochachse liegen. Wenn man für w alle reellen Zahlen zulässt, ist die Menge der Bildpunkte die Menge aller
Punkte oberhalb von g. Das hat dann die Konsequenz, dass es zu jedem Punkt P der Pseudosphäre unendlich
viele Bildpunkte gibt, was dem Begriff 'Abbildung' widerspricht. Darum wird jeder Punkt P ersetzt durch die
Menge der Paare ( P , n ) mit ganzen Zahlen n. Man stellt sich dabei vor, dass die Pseudosphäre aus unendlich
vielen gleichartigen Schichten besteht, die mit n durchnummeriert werden und so mit einander verbunden sind, dass
beim gelb gezeichneten Nullmeridian die n-te Schicht beim Übergang zum Winkel
in die Schicht mit der Nummer n+1 übergeht. Dies ist ein Konzept, das auf Bernhard Rieman (1826-1866)
zurückgeht. Für die so entstehende riemannsche Fläche definiert die oben angegebene Vorschrift auch mit
allen reellen Zahlen als Definitionsbereich eine eindeutige Abbildung. Die zu einem gehörige Zahl n
ist dabei die ganze Zahl, für die gilt. Im Klein-Modell ist die Bildmenge der riemannschen
Fläche die Menge der Punkte innerhalb der gelb-grau gezeichneten Ellipse. Wählt man an Stelle der Konstanten
0,2 in der Abbildungsvorschrift zum Klein-Modell eine kleinere positive Zahl, so wird diese Ellipse größer, bleibt
aber stets kleiner als der schwarz gezeichnete Einheitskreis. Innerhalb der Ellipse sind durch gelb-graue Strecken
Sektoren eingezeichnet, die zu verschiedenen Werten von n gehören.

Die einfachsten Geodäten sind die Meridiane der Pseudosphäre, die sich durch Drehung des gelben Null-
Meridians in Form einer Traktrix um die z-Achse ergeben. Ihre Bilder sind im Poincare-Modell Halbgeraden
auf den Parallelen zur Hochachse und im Klein-Modell Strecken mit dem Endpunkt (-1 ; 0). Jede andere
Geodäte hat genau einen Punkt S, in dem sie einen Meridian senkrecht schneidet. Sie ist dann symmetrisch
zu der Ebene durch diesen Meridian und der z-Achse. Wenn der Punkt S auf dem Null-Meridian liegt mit
dem Abstand von der z-Achse, dann ist die Geodäte ein Abschnitt der Kurve, deren senkrechte Projektion
auf die x-y-Ebene in Polarkoordinaten (r ; w) die Gleichung hat. Die Punkte dieser Kurve lassen
sich durch kartesische Paare 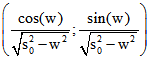mit beschreiben. Dabei
ist bemerkenswert, dass die Geodäte bei genügend großem Wert von beliebig viele Schleifen bilden kann.
Die Bilder dieser Geodäten sind im Poincare-Modell Kreisbögen mit Zentren auf der Rechtsachse und Strecken
im Beltrami-Klein-Modell.

Der weiße Punkt P mit dem daran anhängenden Geschwindigkeitsvektor durchläuft in der Animation die
Geodäte mit konstanter Geschwindigkeit 1. In den beiden Modellen sind die Geschwindigkeiten der Bildpunkte
von P nicht konstant. Mit P als Zentrum wird ein Kreis mitgeführt, der in der perspektivischen Verzerrung als
Ellipse erscheint. Diesem Kreis entspricht im Poincare-Modell ein die Rechtsachse berührender Kreis um den
Bildpunkt von P und im Klein-Modell eine Ellipse mit dem Bildpunkt als Zentrum mit unterschiedlicher Form.
Jeder von der Spitze des Vektors verschiedene Punkt T auf diesem Kreis bzw. auf dieser Ellipse ist der Endpunkt
eines Geschwindigkeitsvektors, der sich ergeben würde, wenn P sich an seinem aktuellen Ort mit der
Geschwindigkeit 1 in eine andere Richtung bewegen würde. Der Kreis bzw. die Ellipse ist also nicht das Bild des
Kreises um P bei den oben angegebenen Abbildungen.

Die Schnittkurven der Pseudosphäre mit Ebenen sind keine Geodäten. Darum sind die Bilder der
Schnittkurven im Beltrami-Klein-Modell nicht geradlinig und im Poincare-Modell keine Kreisbögen zu
Halbkreisen, die senkrecht auf der Rechtsachse stehen.