Es lebe die Geometrie!

Fourieranalyse der Dreiecke

Zur Theorie der Fourieranalyse der Dreiecke siehe

http://www.vivat-geo.de/Pdf-Dateien/Fourierdreieck.pdf

und für beliebige Vielecke

https://www.vivat-geo.de/Pdf-Dateien/Fourierneck.pdf

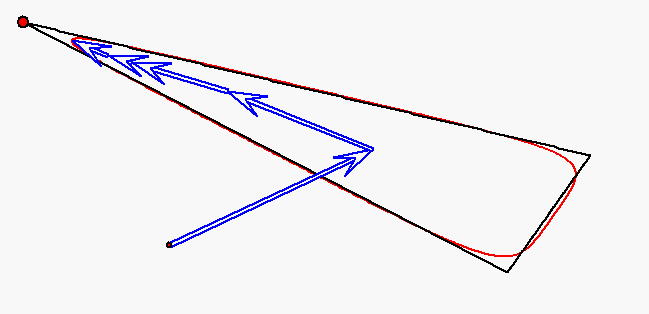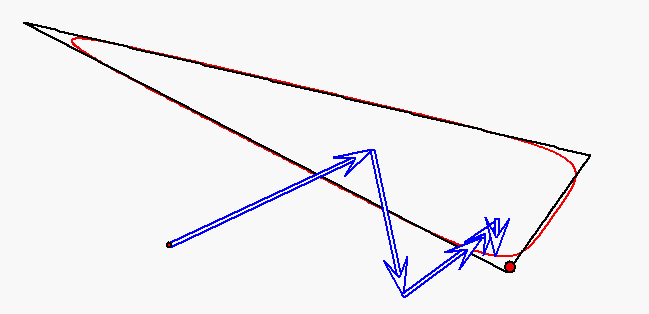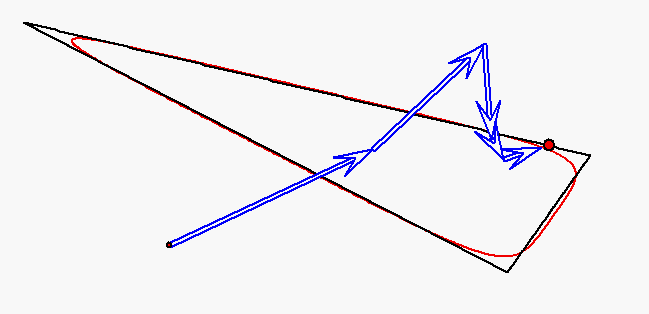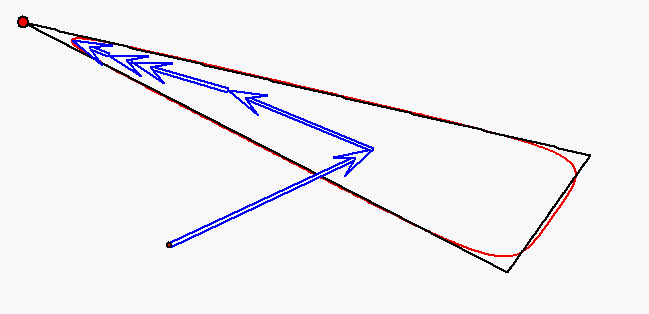
Der rote Punkt durchläuft das Dreieck auf den Seiten mit jeweils konstanter
Geschwindigkeit, aber so, dass die Durchlaufzeiten für alle Seiten gleich sind.
Die Bewegung dieses Punktes wird durch
gleichförmige Kreisbewegungen mit den Winkelgeachwindigkeiten
, , und approximiert (Fourier-Approximation).
Dabei ist , wobei T die Umlaufzeit des Punktes auf dem Dreieck ist.

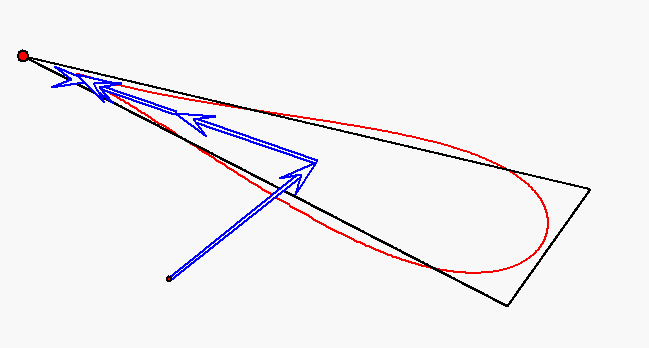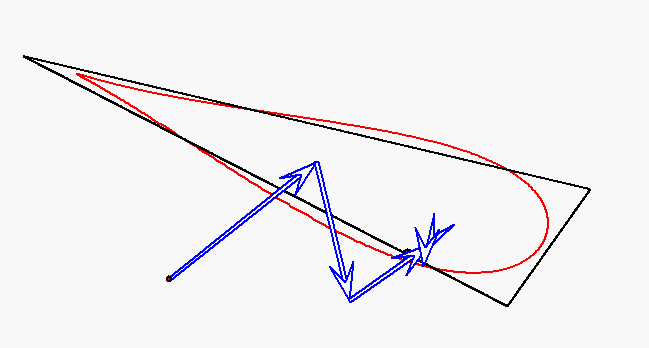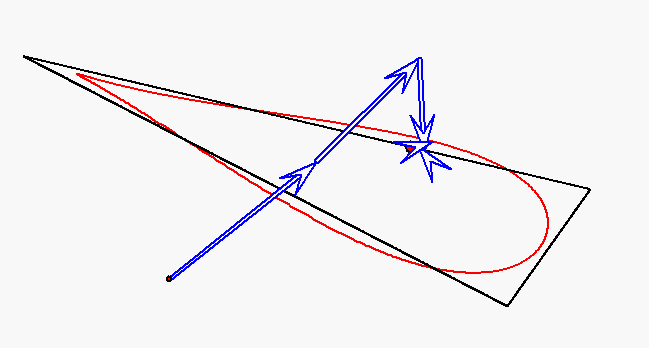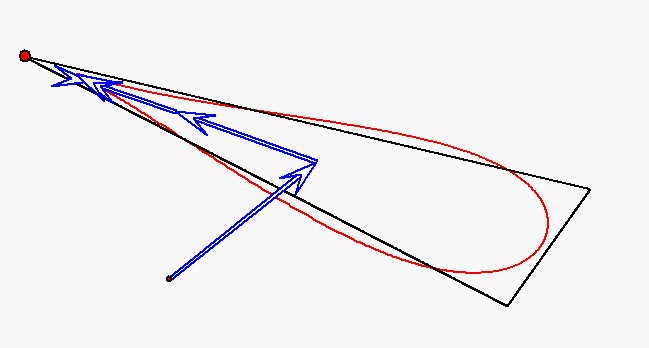
Der rote Punkt durchläuft das Dreieck auf allen Seiten mit derselben
konstanten Geschwindigkeit. Die Bewegung dieses Punktes wird durch
gleichförmige Kreisbewegungen mit den Winkelgeachwindigkeiten
0, , , und approximiert (Fourier-Approximation).

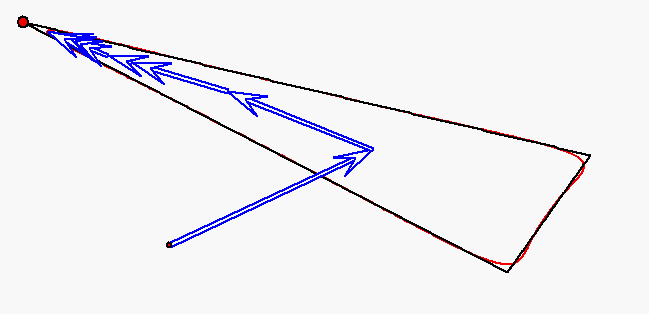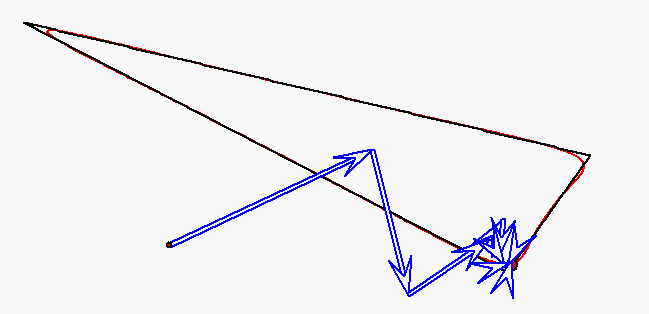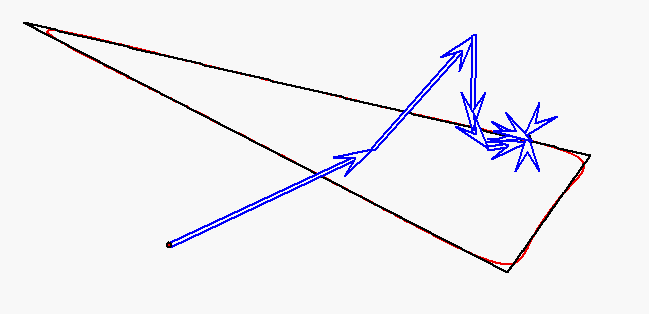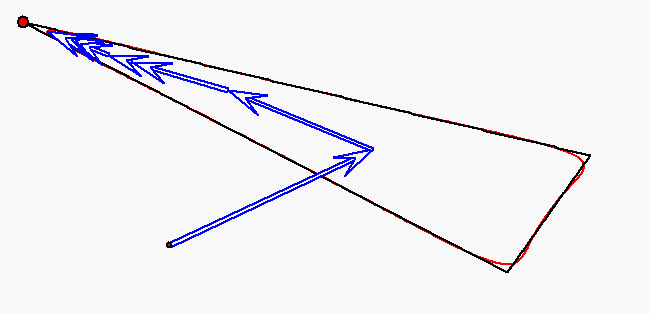
Der rote Punkt durchläuft das Dreieck auf den Seiten mit jeweils konstanter
Geschwindigkeit, aber so, dass die Durchlaufzeiten für alle Seiten gleich sind.
Die Bewegung dieses Punktes wird durch
gleichförmige Kreisbewegungen mit den Winkelgeachwindigkeiten
0, , , , , , , und approximiert (Fourier-Approximation).