Es lebe die Geometrie!

Kachelungen im Kreis-Modell, die mit Nachbar-Bewegungen
aus einem Dreieck mit der Signatur 123 erzeugt werden

Ähnlich wie in der euklidischen Ebene kann man auch in der hyperbolischen Ebene Kachelungen durch
Nachbar-Bewegungen aus einem geeigneten Vieleck erzeugen. Wir sprechen dann von eine Kachelung,
wenn die ganze hyperbolische Ebene durch Kacheln überdeckt ist, die keine inneren Punkte gemeinsam
haben. Da dafür unendlich viele Kacheln nötig sind, können in den folgenden Zeichnungen nur Teil-
Kachelungen dargestellt werden, die aber beliebig ergänzbar sind. Die Möglichkeiten für Kachelungen sind
in der hyperbolischen Geometrie wesentlich vielfältiger als in der euklidischen. Denn die Anzahl der Ecken
des Ausgangs-Vielecks, an denen mehr als zwei Kacheln zusammentreffen, ist nicht notwendig kleinergleich
6, sondern beliebig groß. Außerdem gibt es weniger Beschränkungen bei der Größe der Innenwinkel des
Vielecks.

Die Möglichkeit der Erzeugung von Kachelungen durch Nachbar-Bewegungen beruht auf folgendem Satz,
der sowohl für die euklidische, als auch für die hyperbolische Geometrie (mit reelwertigen Koordinaten) gilt.

Satz : Ggegeben sei eine Gerade g mit einem Punkt P darauf und eine Gerade h durch einen Punkt Q. Dann
gibt es genau vier Bewegungen, die P in Q und g in h abbilden. Wenn B1 und B2 zwei derartige Bewegungen
sind, dann sind sie gleich oder B2 entsteht aus B1 dadurch, dass hinter B1 die Spiegelung an h, an Q oder
der Senkrechten zu h durch Q angewandt wird.

Dabei ist eine Bewegung (oder Kongruenz-Abbildung) eine Abbildung der Punktmenge auf sich mit
folgenden Eigenschaften:
Die Punktmenge einer Geraden wird auf die Punktmenge einer Geraden abbildet.
Die Bildpunkte zweier Punkte P und Q haben den gleichen Abstand wie P und Q.
Die Bilder zweier Geraden g und h schließen einen gleich größen Winkel ein wie g und h.

Eine Nachbar-Bewegung zu einer Kachel K0 ist eine Bewegung, die K0 in eine Kachel K1 abbildet, die
genau die Punkte einer Seite von K0 mit K0 gemeinsam hat. Aus dem Satz folgt, dass es zu jeder Seite
höchstens zwei derartige Nachbar-Bewegungen geben kann. Davon ist die eine gerade, lässt sich also
durch eine Hintereinanderschaltung von einer geraden Anzahl von Achsen-Spiegelungen darstellen und
die andere ungerade.

Die Bedeutung der Begriffe 'Punkt', 'Gerade', 'Abstand' und 'Winkelgröße' soll im Folgenden erklärt werden.
Siehe auch die Pdf.Datei ' Die Pseudosphäre und die hyperbolische Geometrie'

Wir benutzen hier zur Darstellung der hyperbolischen Geometrie das Kreis-Modell nach Poincare. Die 'Punkte'
dieses Modells sind die Punkte der euklidischen Ebene im Innern eines Einheitskreises. Die Punkte auf dem
Einheitskreis ('Enden' genannt) sind keine 'Punkte'. Die 'Geraden' des Modells sind die Kreisbögen, die der
Einheitskreis aus dazu orthogonalen Kreisen herausschneidet, oder die Strecken, die er aus den Geraden durch
sein Zentrum N ausschneidet. Die Geraden duch N betrachten wir im Zusammenhang mit dem Poincare-Modell
als Kreise mit unendlich großem Radius.

Das Kreis-Modell nach Poincare hängt eng mit dem Beltrami-Klein-Modell der hyperbolischen Geometrie
zusammen. In diesem Modell sind die 'Punkte' ebenfalls die Punkte der euklidischen Ebene im Innern des
Einheitskreises, die 'Geraden' aber alle Strecken, die der Einheitskreis aus den ihn treffenden Geraden heraus=
schneidet. Jedem 'Punkt' P des Poincare-Modells ist in folgender Weise ein 'Punkt' P' des Beltrami-Klein-
Modells zugeordnet: Wenn a der Abstand des Einheitkreis-Mittelpunktes N von P ist, dann hat P' den Abstand
von N, und P liegt auf der Strecke NP'. Drei Punkte P', Q' und R' sind dann im Beltrami-Klein-Modell
genau dann kollinear (liegen also auf einer euklidischen Geraden), wenn die Punkte P, Q und R im Poincare-
Modell kollinear sind, also auf einem Kreis liegen, der orthogonal zum Einheitskreis ist.

Im Poincaré-Modell stimmt das Winkel-Maß mit dem euklidischen Winkel-Maß für Kreise überein. Die Größe
eines Winkels P'Q'R' im Beltrami-Klein-Modell ist durch die Größe des entsprechenden Winkels PQR im
Poincaré-Modell gegeben. (PQ und QR sind im Beltrami-Klein-Modell geradlinige Strecken und im Poincare-
Modell Kreisbogen.)

Abstände lassen sich im Beltrami-Klein-Modell leichter definieren als im Poincaré-Modell. Sind nämlich E' und
F' die Enden einer 'Geraden' g' im Beltrami-Klein-Modell, M' der Mittelpunkt der Strecke E'F' und P' ein
weiterer 'Punkt' darauf, dann ist der signierte Abstand von P' und M' durch 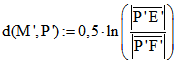mit den
euklidischen Streckenlängen und gegeben. Dabei ist genau für Punkte P', die näher
bei E' als bei F' liegen. Für einen beliebigen Punkt Q' auf E'F' wird definiert: .
Der unsignierte Abstand von Q' und P' (meist nur 'Abstand' ohne Attribut genannt) ist dann der Betrag von
d(Q',P'). Im Poincaré-Modell stimmt der Abstand von Q und P mit dem von Q' und P' im Beltrami-Klein-Modell
überein. Aus dieser Abstandsbestimmung folgt, dass P der (hyperbolische) Mittelpunkt von NP' ist, und zwar
sowohl im Poincare-Modell, als auch im Beltrami-Klein-Modell.

Die Animation zeigt die Entwicklung einer Kachelung im Poincaré-Modell bei einer dreieckigen Ausgangs-
Kachel K0 mit den Innenwinkeln 70°, 20° und 30° und der Signatur 123. Auf den folgenden Seiten werden
Kachelungen für die weiteren Signaturen -1-2-3, 1-23, 1-2-3, 321, 3-21, -32-1 und -3-2-1 dargestellt
und erklärt. Damit werden im Wesentlichen alle möglichen Signaturen bei Dreiecken erfasst. Die Signatur
hat in der hyperbolischen Geometrie die gleiche Bedeutung wie die Signatur in der euklidischen Geometrie,
die in der Pdf-Datei ' Kachelungen, die mit Nachbar-Bewegungen erzeugt werden' beschrieben wird.

Bei der Signatur 123 entsteht jede Nachbar-Kachel einer Kachel K durch (hyperbolische) 180°-Drehung
von K um eine (hyperbolische) Seitenmitte von K. Die Seiten der Kacheln sind von 1 bis 3 gegen den
Uhrzeigersinn durchnummeriert, beginnend bei der Seite mit der halben Pfeilspitze. Der Durchlauf im
Uhrzeigersinn legt für jede Seite eine Spitze fest. Wir betrachten den Halbpfeil an der Seite Nummer 1 als
Teil der Kachel, unterscheiden also Kacheln mit gleicher Punktmenge aber unterschiedlicher Nummerierung.

An die Seite 3 von K0 mit der Spitze im Einheitskreis-Mittelpunkt N wird das Bild K1 von K0 bei Drehung
um die Mitte von Seite 3 angelegt, so dass die Seite 3 von K1 auf die Seite 3 von K0 fällt, aber mit ihrer Spitze
am andern Ende. N ist in K1 die Spitze der Seite 2. Die nächste Kachel K2 entsteht durch 180°-Drehung von
K1 um die Mitte ihrer Seite 2, so dass dann die Spitze der Seite 1 von K2 auf N trifft. Dies wird durch
folgendes Ketten-Schema dargestellt:

Das Paar steht für die Seite 3 der Kachel K0, deren zugehörige Bewegung B3 diese Seite so auf sich
selbst abbildet, dass daraus K1 entsteht. (B3 ist also die hyperbolische 180°-Drehung um die hyperbolische
Mitte von Seite 3.) Die zweite Zahl eines Paars gibt stets die Zahl der Signatur an, deren Platznummer darin
durch die erste Zahl des Paars bestimmt wird. Die Größen geben die Winkel zwischen den Seiten
an, die durch die Paare beschrieben werden. Im Schema ist die Zahl am Ende eines Pfeils stets um 1 kleiner
als die Zahl links vom Pfeil, wobei 0 mit 3 identifiziert wird. Da sich das oben beschriebene Ketten-Schema
periodisch fortsetzt, kann eine Kachelung nur dann gelingen, wenn die 'Eckenbedingung'
gilt mit einer ganzen Zahl n größer als 2, da es sonst zu Überlappungen kommen würde. n = 2 ist unmöglich,
da in einer hyperbolischen Ebene die Summe der Innenwinkel-Größen stets kleiner als 180° ist. (In einer
hyperbolischen Ebene gibt es zu jeder Innenwinkelsumme zwischen 0° und 180° ein Dreieck, nicht jedes
führt aber zu einer Kachelung.) Beim den Dreiecken der Animation ist n = 3, die Innenwinkel-Summe 120°.

Oben wurde das Ketten-Schema für den Eckpunkt Nummer 3 an der Spitze der 3. Seite angegeben. Um
alle einschränkenden Bedingungen dafür zu finden, dass eine Ausgangs-Kachel bei einer bestimmten
Signatur eine Kachelung erzeugt, muss man die Ketten-Schemata für alle Eckpunkte der Ausgangs-Kachel
untersuchen. Dafür reicht es, dass jede Seiten-Nummer als erste Zahl eines Paars vorkommt. Da im obigen
Schema die ersten Zahlen in den Paaren 3, 2 und 1 sind, ist es nicht nötig, zwei weitere Schemata mit den
Startseiten 2 und 1 zu untersuchen. Die Bedeutung der Eckenbedingungen zeigt folgender

Satz : In einer hyperbolischen Ebene sei ein konvexes Vieleck mit nummerierten Seiten und dazu
eine Signatur gegeben. Wenn für die Innenwinkel-Größen des Vierecks die Eckenbedingungen
für alle Eckpunkte erfüllt sind, dann erzeugt das Vieleck eine Kachelung.
(Quellen: [1] Caratheodory, C., Funktionentheorie II, Birkhäuser Verlag Basel 1961
[2] Iversen, B., Hyperbolic Geometry, Cambridge University Press 1991
In [1] wird ein Beweis für Dreiecke mit der Signatur -1-2-3 gegeben, der für andere
Signaturen übertragbar ist. Zu anderen Vielecken siehe [2])

Für die Kachelungen ist ein weiterer Satz bedeutsam, dessen Beweis sehr viel einfacher ist.
Satz: Wenn eine Kachelung von Nachbar-Bewegungen erzeugt wird, dann bildet jede Nachbar-Bewegung
einer beliebigen Kachel K1 nicht nur K1 auf eine benachbarte Kachel ab, sondern jede andere Kachel K2
auf eine dritte Kachel K3 der Kachelung, die allerdings im Allgemeinen nicht zu K2 benachbart ist. Außerdem
kann jede Nachbar-Bewegung von K2 durch eine Hintereinanderschaltung von Nachbar-Bewegungen von
K1 dargestellt werden.

Die auf die Animation in der Gleitschau anschließende Bilder haben folgende Bedeutung:

Das 1. Bild zeigt im Beltrami-Klein-Modell die Kachelung, welche der in der Animation entspricht. Jeder Punkt
P ist also mit gleicher Farbe durch den von N weiter entfernten Punkt P' ersetzt worden.

Das 2., 3. und 4.Bild zeigt die Kränze mit den Nummern 0, 1 und 2. Die ersten beiden Kränze treten bei dem in
der Animation verwendeten Ansetzverfahren auf; sie werden dort durch einen weißen Rand getrennt. Das 5. Bild
zeigt die Zusammenschau der drei Kränze.

In 6. Bild wurden zu dem äußeren Rand des Kranzes Nr. 2 die vollständigen Seitenkreise gezeichnet. Es
zeigt sich, dass keiner dieser Kreise einen Punkt der drei Kränze im Innern enthält, was bedeutet, dass die
Vereinigungsmenge der drei Kranze eine hyperbolisch konvexe Menge ist. Die entsprechende Menge im
Beltrami-Klein-Modell ist sogar im gewöhnlichen Sinn konvex, d. h. mit zwei Punkten der Menge gehören
alle Punkte auf der Strecke dazwischen ebenfalls zur Menge. Der Grund für die Konvexität liegt darin, dass
in den Eckpunkten am Außenrand jedes Kranzes stets zwei oder drei Kacheln zusammentreffen und deren
Innenwinkelsumme an dieser Ecke , also insbesondere kleiner als 180° ist. Dies Letztere
gilt auch im Beltrami-Klein-Modell für die euklidische Innenwinkelsumme in den Eckpunkten des Außenrandes
der Kränze. Mit Hilfe dieser Erkenntnis kann man begründen, dass aus einem Dreieck, für das die
Eckenbedingung mit natürlichem n>2 gilt, durch Spiegelungen an den Seitenmitten
stets eine Kachelung der ganzen hyperbolischen Ebene entsteht, es also nicht zu Überlappungen mit
gemeinsamen inneren Punkten verschiedener Kacheln kommt.

Im 7. Bild sind zu den Kacheln der Animation die Verbindungen der Seitenmitten farbig gezeichnet. Diese
Kreisbögen schließen in der vollständigen Kachelung zu hyperbolischen Geraden in drei Scharen in den Farben
Rot, Grün und Blau zusammen. Gleichfarbige Geraden schneiden sich dabei nie. Die drei Scharen zerlegen die
hyperbolische Ebene in eine Kachelung mit Dreiecken und Neunecken, die jeweils kongruent sind.


Die Bilder Nr. 8 bis 12 zeigen Kachelungen zur Signatur 123 mit verschiedenen Winkeln.