Es lebe die Geometrie!

Das Berührproblem von Apollonios 2

Das Berührproblem von Apollonios von Perge wurde auf der vorhergehenden Seite mit Hilfe von
Laguerre-Spiegelungen zu drei Zylinder-Ellipsen D*, E* und F* dargestellt, deren Ebenen einen
gemeinsamen Punkt C0 im Innern des Zylinders haben. Auf dieser Seite soll der Fall betrachtet
werden, dass C0 außerhalb des Zylinders liegt. Dann gibt es keine Laguerre-Spiegelung, die C0 in
den Koordinaten-Ursprung abbildet. C0 kann dann aber in einen unendlich fernen Punkt abgebildet
werden, zum Beispiel in den unendlich fernen Punkt auf der y-Achse. Das bedeutet, dass die
Ebenen der Bilder von D*, E* und F* parallel zur y-Achse verlaufen. Das Problem, zu D*, E*
und F* Zylinder-Ellipsen B1* und B2* zu finden, die alle drei Ellipsen berühren, wird so in das
entsprechende Problem für die Bild-Ellipsen transformiert, das einfacher zu lösen ist. Auf der
vorhergehenden Seite zeigte sich die Vereinfachung bei Spiegelung in den Ursprung darin, dass
die zu den Bild-Ellipsen zugehörigen Zykeln Null-Zykeln waren, also zu Kreisen mit dem Radius
Null gehörten, die nur aus einem Punkt bestehen. Dann reduzierte sich das Problem auf die
Bestimmung eines Kreises durch drei Punkte. Im Fall, dass C0 außerhalb des Zylinders liegt, ist
die Vereinfachung nicht ganz so groß.

Die Animation zeigt zu Beginn drei Zykeln ZD*, ZE* und ZF* , die Bilder der Zylinder-Ellipsen
D*, E* und F* bei der Blaschke-Abbildung sind. Die Ebenen dieser Ellipsen schneiden sich in dem
Punkt C0 in der Mitte der magentafarbenen Strecke A0B0. Bei dieser Projektion bildet die Gerade
durch den Koordinatenursprung und den Augenpunkt mit der xy-Ebene einen Winkel von 80°. Die
Strecke A0B0 verläuft parallel zur y-Achse. Die magentafarbene Gerade g ist wie auf der vorigen
Seite die zur Ursprungsgerade durch C0 gehörige Nullpolare, die in der xy-Abene liegt. g ist die
Zykel-Achse der Laguerre-Spiegelung an C0, die jede der drei Zylinder-Ellipsen D*, E* und F*
auf sich abbildet. Bei der durch diese Laguerre-Spiegelung bewirkten Abbildung der zu den Ellipsen
gehörigen Zykeln ZD*, ZE* und ZF* werden darum auch diese auf sich abgebildet. g schneidet
die y-Achse in dem Punkt Z0, der Zentrum der eingezeichneten Orthogonal-Kreise zu ZD*, ZE*
und ZF* ist.

In dem ersten der vier Abschnitte der Animation werden Zykeln ZD, ZE und ZF gezeigt. Sie gehören zu
Zylinder-Ellipsen D, E und F, die Bilder von D*, E* und F* bei der Spiegelung an dem magentafarbenen
Punktes A sind, der sich auf der Strecke A0B0 in Richtung A0 bewegt. Sei Quadrupel
von A, f die symmetrische Bilinearform , F die Matrix mit den Zahlen
1;1;0;-1 in der Hauptdiagonalen und sonst Nullen, die Matrix mit 1;1;1;1 in der Hauptdiagonalen und
sonst Nullen und ( die schwarzen Buchstaben f und F müssen hier von den
blauen unterschieden werden). Dann ist das Quadrupel des Bildes eines Punktes P mit dem Quadrupel
gleich . Wenn Quadrupel der Ebene der Zylinder-Ellipse E ist, dann
ist das Quadrupel des Bildes durch gegeben mit der transponierten Matrix
.

sei das Quadrupel des Punktes C0. Da C0 auf E liegt, ist .
Entsprechendes gilt für die Ellipsen D und F. Das zu A0 gehörige Quadrupel ist
und beim zu B0 gehörigen Quadrupel ist nur das Vorzeichen der Wurzel geändert. Wenn das Spiegelungs-
Zentrum A den Endpunkt A0 erreicht hat, ist die zweite Koordinate der Quadrupel von D, E und F gleich
Null. Dies bedeutet, dass der unendlich fernen Punkt U auf der y-Achse mit dem Quadrupel (0;1;0;0) dann
auf den drei zugehörigen Ebenen liegt. U ist das Bild von C0 bei der Spiegelung an A0. Auf Grund des
Zusammenhangs, der auf der Seite 'Nullpolatität' dargestellt ist, gibt die zweite Komponente eines Ebenen-
Quadrupels mit dritter Komponente 1 die x-Komponente des Mittelpunkts vom Kreis an, der zum
zugehörigen Zykel gehört. Darum liegen die Mittelpunkte der Zykeln ZD, ZE und ZF auf der y-Achse, wenn
A den Endpunkt A0 erreicht hat. Auf dem Weg dorthin haben die drei Zykeln zwar ihren Radius verändert,
die Orthogonalkreise mit dem Zentrum Z0 blieben aber gleich. Der y-Wert von Z0 ist .

Zu den Zykeln ZD, ZE und ZF mit den Mittelpunkten auf der y-Achse wird unten auf dieser Seite ein
Konstruktionsverfahren zur Bestimmung der beiden gemeinsamen Berühr-Zykel mit Zirkel und Lineal
angegeben. Zunächst soll aber eine Berechnungs-Formel dafür angegeben werden. Wir gehen von den
Quadrupeln , und der zugehörigen Ebenen aus. M2
sei die Matrix, die aus der Matrix mit den drei Zeilen d, e und f dadurch entsteht, dass man die zweite
Spalte streicht. N1 bzw. N4 entsteht aus M2, indem man die erste bzw. vierte Spalte durch die Spalte
mit den Formwerten , und ersetzt. Sei f* die Funktion, für die
gilt und Analoges für und . Die Ellipsen
D und E und die Zykeln ZD und ZE berühren sich genau dann, wenn gilt. Eine Ebene zu
einer Ellipse B1, die alle drei Zylinder-Ellipsen D, E und F berührt, hat dann das Quadrupel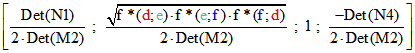
,
vorausgesetzt, dass die Wurzel reell ist. Durch Änderung des Vorzeichens vor der Wurzel ergibt sich die
zweite Berührebene.

Im zweiten Abschnitt der Animation bewegt sich das Spiegelungs-Zentrum A zurück bis zu Punkt C0.
Um dabei B1 mitzunehmen, benutzt man die Hintereinanderschaltung der Laguerre-Spiegelungen
an A0 und an A. Bemerkenswert ist dabei, dass sich dabei jeder Berührpunkt auf einem Kreis mit
dem Mittelpunkt auf der y-Achse bewegt. Im dritten und vierten Abschnitt werden die Abläufe des
ersten und zweiten mit B0 an Stelle von A0 wiederholt. Dabei werden im vierten Abschnitt beide
Berühr-Zykeln mitgenommen. In den Standbildern im Anschluss an die Animation erkennt man, dass
sich die drei Verbindungsgeraden entsprechender Berührpunkte der beiden Berühr-Ellipsen in einem
Punkt treffen, nämlich dem Punkt, der sich bei Spiegelung von C0 an A ergibt.

Im Folgenden soll auf dieser Seite eine Möglichkeit gezeigt werden, Berührzykel mit Zirkel und Lineal
zu konstruieren, wenn die Mittelpunkte der Zykel zu den Zylinder-Ellipsen D, E und F auf einer Geraden
liegen, zum Beispiel auf der y-Achse. Dazu wird das Apollonios-Problem zunächst in zwei Schritten
vereinfacht. In der folgenden Animation wird gezeigt, wie zu drei Zykeln die Berührzykel gefunden
werden können, wenn man weiß, wie das Problem gelöst werden kann, falls einer der Zykeln ein Null-
Zykel ist, also den Radius Null hat. In der darauf folgenden Animation wird dargestellt, wie man das
Problem für drei Zykel mit kollinearen Mittelpunkten auf einer Geraden g lösen kann, wenn man die
Lösung für den Fall kennt, dass einer der drei Zykel durch eine Gerade senkrecht zu g ersetzt wird.

Die Animation zeigt, dass sich sich die Kegelspitzen der Berühr-Zykeln zu ZD, ZE und ZF
um den gleichen z-Wert verändern wie für ZD, ZE und ZF, vorausgesetzt dieser z-Wert ist
bei allen drei Zykeln gleich. Dies gilt auch dann, wenn die Mittelpunkte von ZD, ZE und ZF
nicht kollinear sind.

Das Startbild dieser Animation zeigt drei Zykeln ZD*, ZE* und ZF* mit ihren gemeinsamen Berühr-
Zykeln ZB1* und ZB2* in kräftigen Farben , die im weiteren Verlauf verblassen, um die Zeichnung
nicht zu überladen. ZD*, ZE* und ZF* werden an dem orangefarbenen Kreis K in die Zykel ZD,
ZE und ZF gespiegelt. Dabei werden ZB1* und ZB2* in Berühr-Zykel ZB1 und ZB2 von ZD, ZE
ZF gespiegelt. Wenn der Mittelpunkt von K dabei auf ZD*, ZE* oder ZF* trifft, ist das Spiegelbild
des getroffenen Zykels eine Gerade. Diese Gerade hat keine Entsprechung bei den Zylinder-Ellipsen.
Bei Annäherung der Geraden durch Zykeln werden Ebenen der zugehörigen Zylinder-Ellipsen immer
steiler und haben als Grenzwert die Ebene mit dem Quadrupel [0,1,0,1] oder [0,1,0,-1].

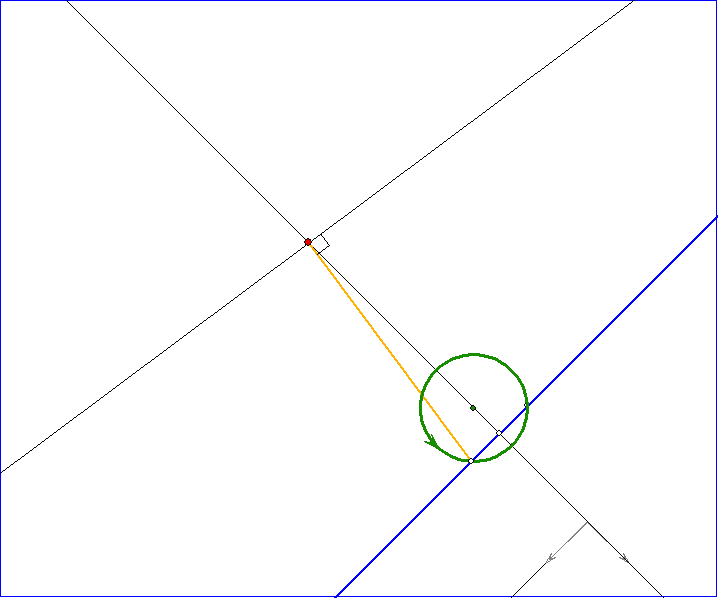
Die Gleitschau zeigt die Konstruktion eines Berühr-Zykels zu einem Null-Zykel ZD, einem weiteren
Zykel ZE und einer Geraden g. Dabei liegt der Mittelpunkt von ZE auf dem Lot h des Punktes ZD
auf g. Die ersten fünf Bildes stellen dies für den Fall dar, dass ZE die Gerade g schneidet, die folgenden
acht Bilder gehen von einem Zykel ZE aus, der nicht schneidet, aber auf der gleichen Seite von g liegt
wie ZD.

Die Begründung für die Konstruktion ergibt sich folgendermaßen:

Es sei d bzw. e der Abstand des Mittelpunktes zu ZD bzw. ZE von g und r der Betrag vom ZE-Radius.
u bzw. v sei der Abstand des Mittelpunkts des gesuchten Berühr-Zykels von h bzw. g. Dann gilt
und , folglich
und .
Der Zähler des Terms zu v ist das Quadrat der Länge der orangefarbenen Strecke j in
beiden Fällen des Schneidens von ZE und g. j verbindet ZD mit dem Punkt C. Um v zu konstruieren
wird der Höhensatz für ein rechtwinkliges Dreieck benutzt, für das die Höhenlänge
angibt. v und sollen dabei die Längen der Höhenabschnitte sein und ZD der Fußpunkt
der Höhe. Dazu wird um ZD ein Kreis mit dem Radius gezeichnet und der Schnittpunkt
A mit der Senkrechten auf j durch ZD bestimmt. Die violette Strecke s, die den dritten Eckpunkt B des
rechtwinkligen Dreiecks ABC mit ZD verbindet, hat die Länge v. Der Mittelpunkt des gesuchten
Berührzykels ist dann Schnittpunkt des Kreises um ZD mit dem Radius v und einer Parallelen zu g
im Abstand v.


Algeraische Lösung des Berührproblems für beliebige Ebenen-Schnittpunkte C0

Wir gehen wieder von den Quadrupeln , und der Ebenen
zu den Zylinder-Ellipsen D, E und F aus, die paarweise verschieden seien. Die Ellipse B mit dem Quadupel
berührt D, E und F genau dann, wenn gilt:
.

Sei zunächst f linear abhängig von d und e.
Dann gibt es eine reelle Zahl r ungleich 0 und 1 mit .
Angenommen sei, dass es eine gemeinsamen Berühr-Ellipse gibt. Wenn man dann die Gleichung

nach auflöst und den Ergebnis-Term in einsetzt, ergibt sich
, folglich . Das bedeutet, dass sich
D und E berühren, ihre Ebenen sich also in einer Geraden g schneiden, die mit dem Zylinder genau einen
Berührpunkt P gemeinsam hat. Auch F berührt dann D und E in P und g liegt in der zu F gehörigen Ebene.
Die Zykel ZD, ZE und ZF haben darum eine gemeinsame Tangente. Dann trennt einer der Zykeln die beiden
anderen, so dass es keinen gemeinsamen Berühr-Zykel geben kann, folglich auch keine gemeinsame Berühr-
Ellipse, im Widerspruch zur Annahme. Da die Annahme also zu verwerfen ist, gilt es keine gemeinsame
Berühr-Ellipse, folglich auch keinen gemeinsamen Breühr-Zykel.

Wir setzen nun im Folgenden voraus, dass d, e und f linear unabhängig sind.
M1, M2 bzw. M4 sei die Matrix, die aus der Matrix mit den drei Zeilen d, e und f dadurch entsteht, dass man
die 1., 2. bzw. 4. Spalte streicht. Wenigstens eine dieser drei Matrizen hat einen Determinanten-Wert ungleich
Null. Wir betrachten den Fall, dass dies für M2 gilt. In den andern Fällen schließt man analog weiter. N1 bzw.
N4 entsteht aus M2, indem man die erste bzw. vierte Spalte durch die Spalte mit den Formwerten
, und ersetzt. Die Ellipse B mit dem Quadupel
berührt D, E und F genau dann, wenn gilt. Daraus folgt

und .
Dies ist ein lineares Gleichungssystem in den Komponenten von b mit der Lösung
;
mit , , , .
kann dann aus der Gleichung


bestimmt werden. Dies ist eine quadratische Gleichung genau dann, wenn ist, und das ist
äquivalent damit, dass der gemeinsame Punkt C0 der Ebenen zu D, E und F nicht auf dem Zylinder liegt.
Das Berührproblem hat dann genau dann eine Lösung, wenn der Term unter der Wurzel im Lösungsterm
der quadratischen Gleichung nicht negativ ist.

Wenn C0 auf dem Zylinder liegt, hat die lineare Gleichung für genau eine Lösung. C0 bestimmt über die
Blaschke-Abbildung eine gemeinsame Tangente für die Zykeln ZD, ZE und ZF . Die Ellipsen D, E und F
treffen sich zwar in C0, haben dort aber keine gemeinsame Tangente, denn d, e und f wären sonst nicht linear
unabhängig. Wir betrachten genauer den Fall, das C0 der Punkt mit den Koordinaten (0;-1;0;1) ist. Dann ist
bei d, e und f die vierte Koordinate gleich der zweiten, folglich und ,
also s = 0, u = 1 und
mit der Lösung . Der Punkt Z mit den Koordinaten-Quadrupel (t;r;0;1) ist Potenz-
Zentrum der Zykeln ZD, ZE und ZF und liegt auf ZB. Man erhält eine in d, e und f symmetrische Darstellung
für b, wenn man die Abkürzungen , , undeinführt. Dann gilt nämlich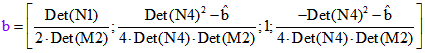
.
Dabei ist . Der Berührzykel ZB entsteht durch Spiegelung der y-Achse
an dem Kreis um Z, der ZD, ZE und ZF (euklidisch) orthogonal schneidet, falls es diesen Kreis gibt.