Es lebe die Geometrie!

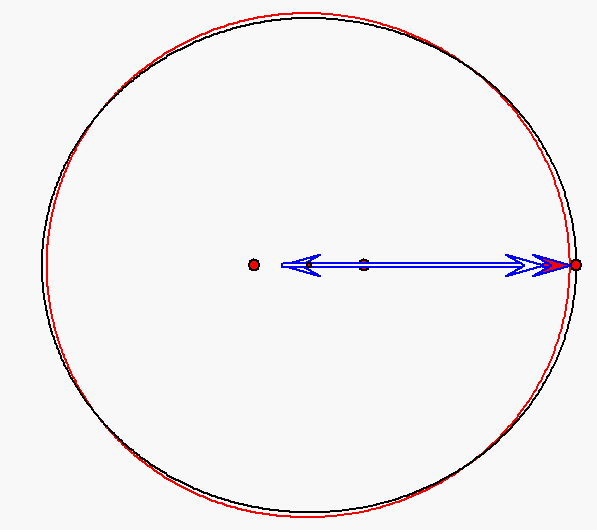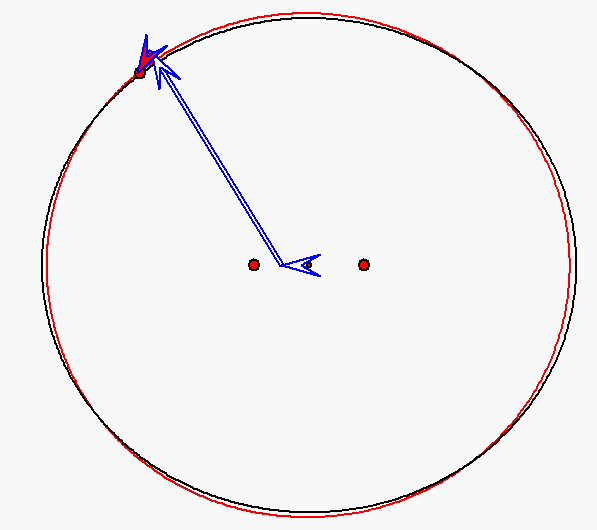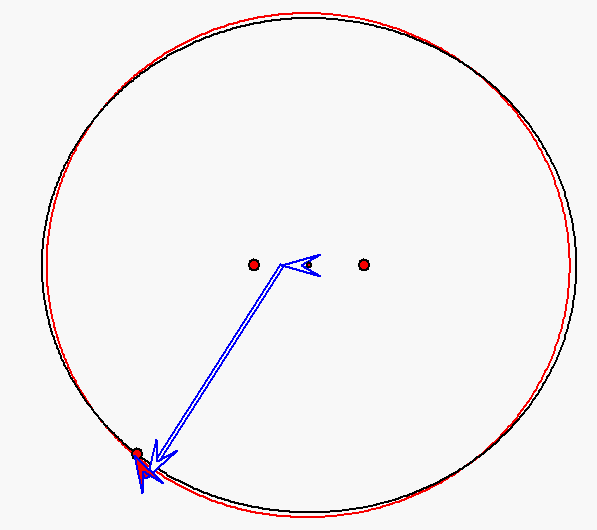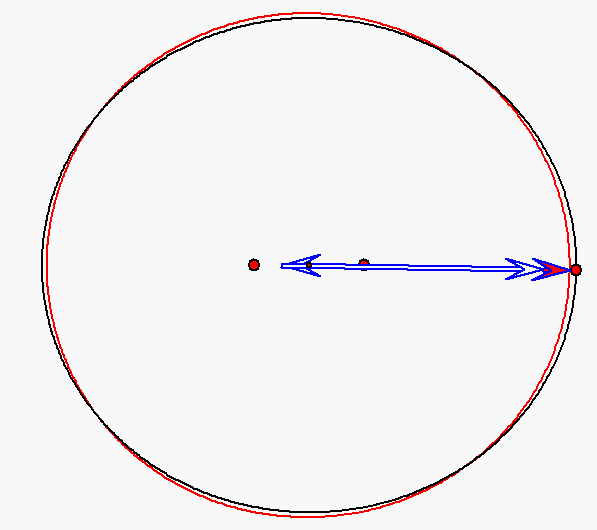
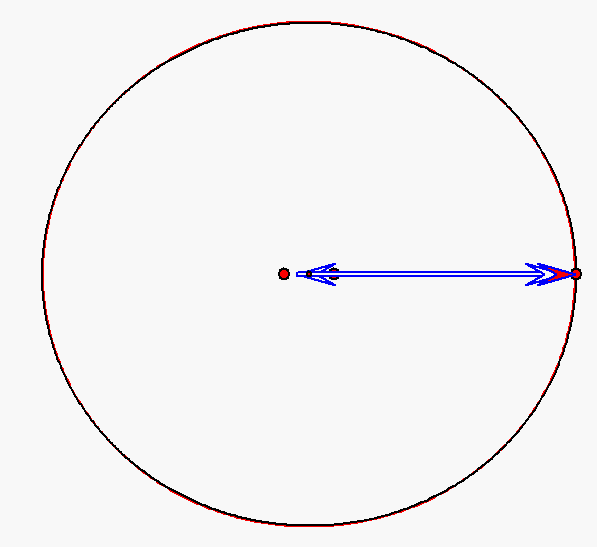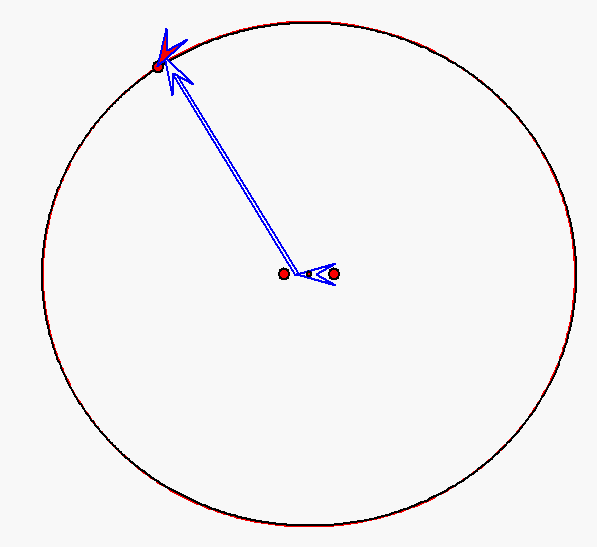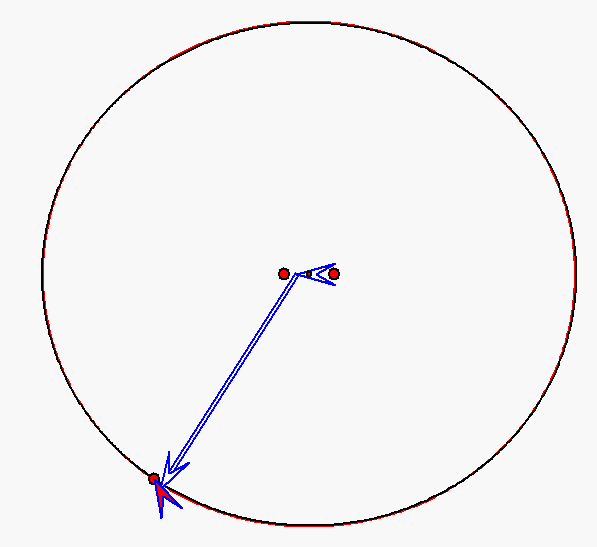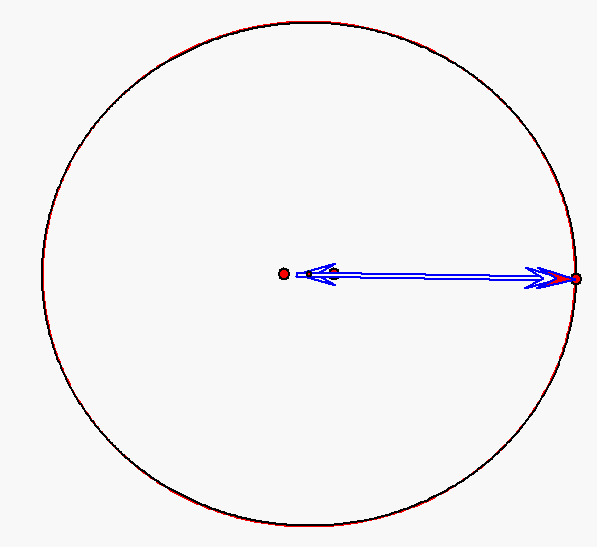
Bewegung nach dem Kopernikus-Modell für den Planeten Merkur (e = 0,206)
mit Pfeilen zu den Nummern 0, 1 und 2. Die Sonne wird hier durch den großen roten Punkt
rechts von der Ellipsenmitte dargestellt, die als kleiner roter Punkt angegeben ist.
Er ist ein Brennpunkt der schwarz gezeichneten Ellipse. Auf dieser Ellipse bewegt sich
der als roter Punkt dargestellte Merkur entsprechend den ersten beiden keplerschen
Gesetzen. Der große rote Punkt links neben der Ellipsenmitte stellt den zweiten Brennpunkt
dar. Er wird als 'Antifokus' der Planetenbahn bezeichnet. Die Spitze des roten Pfeils gibt
die Bewegung nach dem Kopernikus-Modell an. Sie ist eine Überlagerung von
gleichförmigen Kreisbewegungen, die sich dadurch ergibt, dass der kleine rote Pfeil
sich mit konstanter Geschwindigkeit um die Spitze des langen blauen Pfeils dreht,
der sich seinerseits mit konstanter Geschwindigkeit um die Mitte zwischen Ellipsenmitte und
Antifokus dreht. Die Planetenbahn nach dem Kopernikus-Modell ist als rote Kurve eingezeichnet.
Die Exzentrizität der Merkur-Bewegung ist so groß, dass die Abweichung nach dem Kopernikus-Modell
gegenüber der tatsächlichen Bewegung des Planeten gut erkennbar ist. (Nur darum wird die
Bewegung hier dargestellt.) Kopernikus hat dieses Modell beim Merkur nicht benutzt,
wohl aber bei den Planeten Mars, Jupiter und Saturn, und auch in versteckter Form bei der Venus..

Bewegung nach dem Kopernikus-Modell für den Planeten Mars (e = 0,0934)
mit Pfeilen zu den Nummern 0, 1 und 2