Es lebe die Geometrie!

Der Satz von Miquel und der Büschelsatz
für die Kugel und das Hyperboloid

Der Dreiecksatz von Auguste Miquel (1816-1851) besagt:
In einem Dreieck ABC seien auf den Geraden BC, CA, und AB Punkte A*, B* bzw. C* gegeben.
Dann haben die Umkreise der Dreiecke A*BC*, B*CA* und C*AB* einen gemeinsamen Punkt D.
Dieser Satz kann durch stereografische Projektion zu einer Version für die Kugel übertragen werden.
Er ist dann ein Satz über acht Punkte, die auf sechs Kreisen einer Kugel-Oberfläche liegen, wobei
jeder auf drei Kreisen liegt und jeder Kreis vier der Punkte trägt. Man nennt dies eine -Punkt-
Kreis-Konfiguration. Eine analoge Version des Satzes von Miquel gilt auch für das Hyperboloid.

Den Büschelsatz gibt es ebenfalls in einer Fassung für die Kugel, für das Hyperboloid und für die
Ebene. Für die Kugel macht er eine Aussage zu einer -Punkt-Kreis-Konfiguration, die sich
von der zum Satz von Miquel unterscheidet. In der Ebene kann der Büschelsatz folgendermaßen
formuliert werden:
Gegeben seien verschiedene Punkte A , A*, B, B*, C, C* und siebenter Punkt D, der auf den drei
Geraden AA*, BB* und CC* liegt. Wenn dann A , A*, B, B* gemeinsam auf einem Kreis liegen und
B, B*, C, C* auf einem zweiten Kreis, dann liegen die Punkte C, C*, A , A* gemeinsam auf einem
dritten Kreis.

Die folgenden Gleitschauen zeigen die Zusammenhänge zwischen den verschiedenen Versionen
des Satzes von Miquel und des Büschelsatzes.

Die Gleitschau zeigt den Dreieckssatz von Miquel und die Übertragung auf die Kugel durch
stereografische Projektion eines gedachten Dreiecks in der Ebene, welche die Kugel im Nordpol
berührt. Ein verkleinertes Abbild dieses Dreiecks ist unten rechts angegeben. Unter den Punkten
A, B, C, A*, B*, C* und D verstehen wir im Folgenden die Projektions-Bilder der oben mit diesen
Buchstaben bezeichneten Punkte des ebenen Dreiecks. Das Zentrum D* der Projektion liegt im Südpol
der Kugel.

Die acht Punkte A, B, C, A*, B*, C*, D und D* bilden eine ,
weil durch jeden der 8 Punkte 3 Kreise gehen und auf jedem der 6 Kreise 4 Punkte liegen. Die mit
dem Zeichen * versehenen Buchstaben wurden mit dunklerer Farbe gezeichnet und mit einem weißen
Ring markiert. Zwei der Punkte liegen genau dann nicht gemeinsam auf einem der sechs Kreise, wenn
sie in der gleichen Farbart dunkel oder hell dargestellt werden, also A und A*, B und B*, ... Auf
jedem der sechs Kreise gibt es zwei gesternte und zwei ungesternte Punkte, und es kommen alle vier
Farbarten rot, blau, grün und gelb vor. Die sechs Kreise sind rot, blau oder grün in dunklen oder hellem
Farbton gezeichnet. Zwei Kreise haben genau dann keinen der acht Punkte gemeinsam, wenn sie in der
gleichen Farbart gezeichnet sind.

Die letzten drei Bilder der Gleitschau zeigen die Veränderung des Schnitts der dunklen Kreise, wenn D*
nicht mehr auf den Kugel liegt.

Den Satz von Miquel für die Kugel kann man folgendermaßen formulieren:
Gegeben seien sechs Kreise auf einer Kugel in den Farben hellrot (hr), dunkelrot (dr), hellblau (hb),
dunkelblau (db), hellgrün (hg) und dunkelgrün (dg). Es gibt dann acht verschiedene Mengen mit drei
dieser Kreise, bei denen alle drei Farbarten rot, blau und grün vorkommen, nämlich
{ hr , hb , hg }, { dr , db , dg},
{ dr , hb , hg}, {hr , db , hg}, {hr , hb , dg},
{hr , db , dg}, {dr , hb , dg}, {dr , db , hg }
Wenn dann für sieben der acht Mengen gilt, dass die drei Kreise darin genau einen Kugelpunkt gemeinsam
haben, dann gilt dies auch für die achte Menge dreier Kreise.

In der Gleitschau ist D* der Schnittpunkt für { hr , hb , hg } und D der für { dr , db , dg}. Die gesternten
bzw. ungesternten Punkte in den Farben rot, blau und grün gehören zu den Kreis-Mengen mit zwei dunklen
bzw. hellen Kreisen.

Alternative Formulierung des Satzes von Miquel für die Kugel:
Gegeben seien acht verschiedene Punkte A, B, C, A*, B*, C*, D und D* auf einer Kugel.
Es gibt sechs Quadrupel mit diesen Punkten als Komponenten mit folgenden Eigenschaften:
Alle vier Buchstaben A, B, C und D kommen vor.
Die ersten beiden Komponenten sind ungesternt und die letzten beiden gesternt.
Die Reihenfolge im Quadrupel ergibt sich als gerade Permutation der Folge ABCD.
Die ersten beiden Buchstaben sind lexikografisch geordnet (BD statt DB).
Es sind dies die Quadrupel ABC*D*, ACD*B*, BCA*D*, ADB*C*, DBA*C*, CDA*B*.
Wenn fünf dieser Quadrupel zu Punkten mit einem gemeinsamen Kreis gehören, dann auch das sechste.

Diese merkwürdigen Eigenschaften der Quadrupel orientieren sich an einem einfachen Beweis für den
Satz von Miquel mit Hilfe von Doppelverhältnissen. Dazu denken wir uns die acht Kugelpunkte
stereografisch auf eine Ebene projiziert, wobei das Projektions-Zentrum nicht D* und auch kein anderer
der acht Punkte sein soll. Die Bilder der drei Kreise durch D* sind also keine Geraden, sondern ebenfalls
Kreise. Die Punkte der Bildebene beschreiben wir mit lomplexen Zahlen, weil Punkte P, Q, R und S
genau dann hier auf einem Kreis liegen, wenn das Doppelverhältnis der
zugehörigen komplexen Zahlen p, q, r und s eine reelle Zahl, der Imaginärteil also Null ist.
Der Satz von Miquel folgt dann aus der leicht nachrechenbaren Produkt-Gleichung
DV(A,B;C*,D*) DV( A,C;D*,B*) DV(B,C;A*,D*) DV(A,D;B*,C*) DV(D,B;A*,C*) DV(C,D;A*,B*) =1.

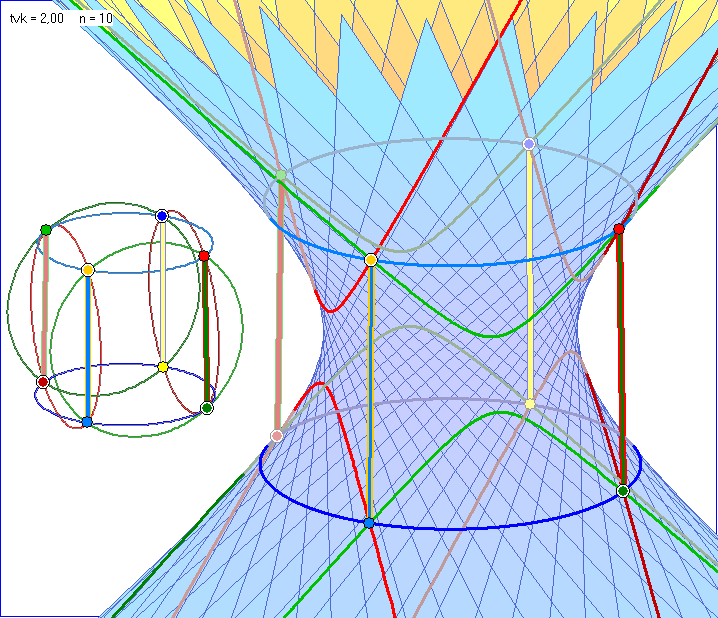
Diese Gleitschau zeigt die Übertragung der Miquel-Figur von der Kugel auf ein Hyperboloid, das mit
einem Basis-Viereck zu den Koordinaten-Tripel (1 ; 0 ; 0), (1 ; 1 ; 1), (0 ; 1 ; 0) und (1 ; 1 ; -1)
konstruiert wurde. Im ersten Bild sind die acht Punkte A, B, C, A*, B*, C*, D und D* Eckpunkte
eines Quaders, links im Bild auf einer Kugel, rechts auf einem Hyperboloid. Die senkrechten Kanten
A*C, BD*, C*A und DB* des Quaders sind in den Farben ihrer Endpunkte auf der Quadrik markiert.
Die Kreise links sind Schnittmengen der Seiten-Ebenen des Quaders mit der Kugel. Die Schnittmengen
der Ebenen mit dem Hyperboloid sind die zwei blauen Kreise und die vier roten oder grünen Hyperbeln.

In den folgenden Bildern der Gleitschau wird zunächst die Teilverhältnis-Konstante tvk dieser Quadrik QH
variiert. Dabei bleiben die Geraden, auf denen die markierten Kanten liegen, unverändert, die Endpunkte
der Kanten werden aber so verschoben, dass sie auf QH liegen. Anschließend werden die Richtungen dieser
vier Geraden bei tvk = 2 verändert, und zwar zunächst so, dass alle vier durch einen gemeinsamen Punkt Z0
gehen. (Er wird als weiß gefüllter kleiner Kreis dargestellt.) Dadurch wird erreicht, dass je zwei benachbarte
dieser Geraden weiterhin in einer Ebene liegen. Da die Punkte auf dem dunkelblauen Kreis unverändert
bleiben, sind dann die Voraussetzungen des Satzes von Miquel weiterhin erfüllt, so dass auch die Punkte
A, B*, C und D* weiterhin auf der hellblauen Ellipse bleiben. In den vorletzten acht Bildern der Gleitschau
werden mehrere Schnittpunkt für die vier Kanten-Geraden zugelassen. Es sind dies der Schnittpunkt Z0 der
Kanten-Geraden A*C und BD*, der auf der Kanten-Gerade BD* frei gewählte Punkt Z1 als Schnittpunkt
von BD* und C*A, sowie der Schnittpunkt Z2 der Ebene durch C*, D und A mit der Kanten-Gerade A*C.

Die Formulierung des Satzes von Miquel für das Hyperboloid kann direkt aus der für die Kugel
übernommen werden, indem man 'Kreis' durch 'Kurve des Schnitts einer Ebene mit dem Hyperboloid'
ersetzt. Die Schnittkurven sind Hyperbeln, Ellipse oder Geraden-Paare, also Kegel-Schnitte. Den
Beweis des Satzes kann man analog wie für die Kugel mit Hilfe von Doppelverhältnissen führen.
Die komplexen Zahlen werden dabei durch anomal-komplexe Zahlen ersetzt. (Man nennt sie auch
'anormal-komplex'.) Die Zuordnung der Punkte des Hyperboloids zu diesen Zahlen wird auf der
vorvorigen Seite ' Hyperboloid 2' erklärt.

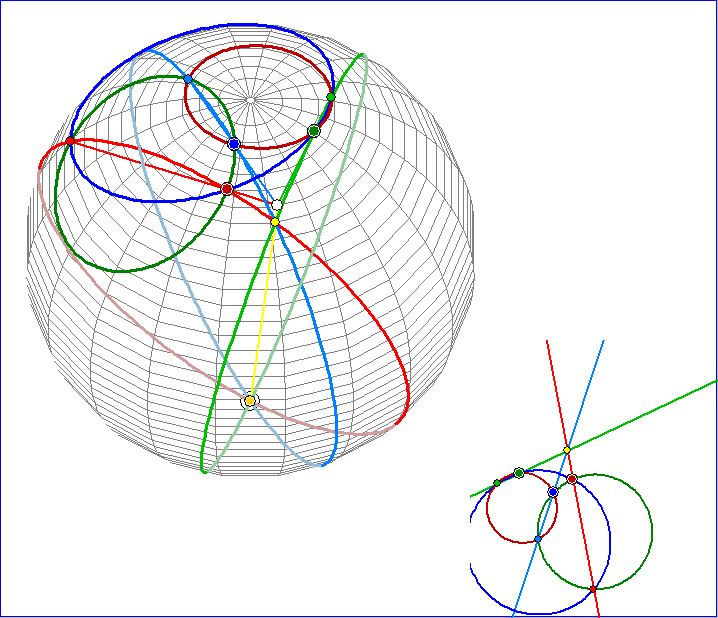
Die Gleitschau zeigt die stereografische Übertragung der Büschelsatz-Figur auf die Kugel. Dabei wurden
Farben wie in der Gleitschau zum Satz von Miquel am Anfang dieser Seite benutzt. Wir verwenden hier auch
die gleichen Buchstaben. Während aber beim Satz von Miquel genau die gesternten und ungesternten Punkte
gleicher Farbart A und A*, B und B*, ... nicht gemeinsam auf einem der sechs Kreise liegen, liegen beim
Büschelsatz diese Punkte sogar gemeinsam auf jeweils drei Kreisen (Assoziation: Fermionen-Bosonen).
Wir nennen die Punkte-Paare AA* und BB* konzyklisch, wenn die vier verschiedenen Punkte A , A*, B, B*
gemeinsam auf einem Kreis liegen. Dann kann man den Büschelsatz für die Kugel folgendermaßen formulieren:

Auf einer Kugel seien Punkte-Paare AA* und BB*, BB* und CC*, CC* und DD*, sowie DD* und AA*
konzyklisch mit verschiedenen Kreisen. Wenn dann AA* und CC* ebenfalls konzyklisch sind, dann auch
BB* und DD*.

In der Zeichnung sind Punkte gleicher Farbart durch eine Strecke in dieser Farbe verbunden, die bis zu dem
Punkt Z weitergeführt wurde, der als weiß gefüllter Kreis dargestellt ist. Dieser Punkt liegt auf allen sechs Kreis-
Ebenen. Um dies unter der Voraussetzung des Büschelsatzes zu zeigen, betrachtet man den einzigen Schnittpunkt
V der Ebenen AA* BB*, BB*CC* und CC*AA* und den einzigen Schnittpunkt W der Ebenen AA* DD*,
DD*CC* und CC*AA*. V liegt auf den Geraden AA*, BB*, CC* und W auf den Geraden AA*,
DD*und CC*. Da beide Punkte auf AA* und CC* liegen, muss V gleich W sein und folglich sowohl auf
BB*, als auch auf DD* liegen.

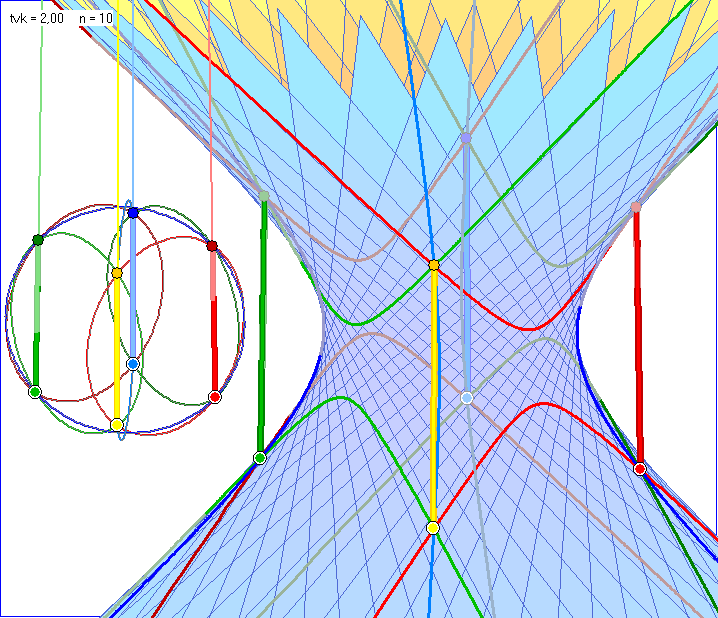
Die Gleitschau startet mit dem entsprechenden Bild wie in der vorvorigen zum Satz von Miquel,
allerdings mit geänderten Farben. Die markierten Strecken bilden die Kanten eines Quaders mit
Eckpunkten auf dem Hyperboloid und links im Bild auf einer Kugel. Anders als beim Satz von
Miquel sind die Kegelschnitte in der Grund- und der Deck-Ebene nicht eingzeichnet, dafür aber
die blauen Kegelschnitte der Ebenen durch die Diagonalen der Grund- und der Deck-Ebene. In
den folgenden Bildern wird zunächst die Veränderung gezeigt, die durch die Parallel-Verschiebung
der Geraden AA* entsteht. Anschließend wird der gemeinsame Punkt Z der Geraden AA*, BB*,
CC* und DD* verrückt.