Es lebe die Geometrie!

Die Koppelkurve und ihre Evolute

Eine Koppelkurve ist die Spur eines Punktes Q mit festem Abstand von den Endpunkten A und B
einer Sehne konstanter Länge, die in einer Ebene bewegt wird. Dabei ist im klassischen Fall die Sehne
die Koppel eines Koppelgetriebes, bei dem A und B auf zwei Kreisen geführt werden. Die Evolute
einer Koppelkurve ist der geometrische Ort der Krümmungs-Mittelpunkte der Kurve. Der zu einem
Punkt Q der Koppelkurve gehörige Krümmungs-Mittelpunkt Q* ergibt sich näherungsweise zum
Beispiel dadurch, dass man benachbarte Punkte P und R auf der Kurve vor bzw. nach Q wählt und
den Schnittpunkt der Mittelsenkrechten von PQ und QR bestimmt. Den exakten Wert für Q* erhält
man durch den Grenzübergang P --> Q und R --> Q.

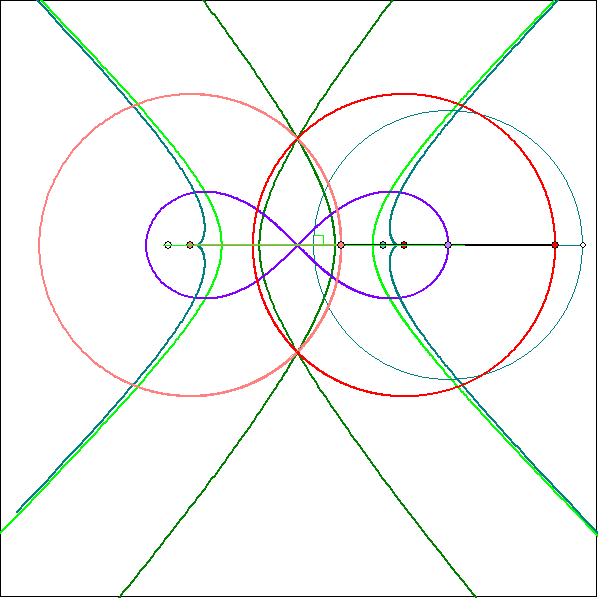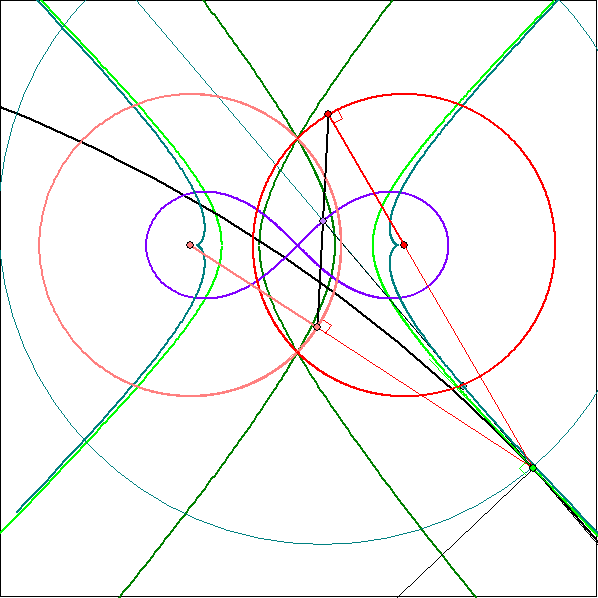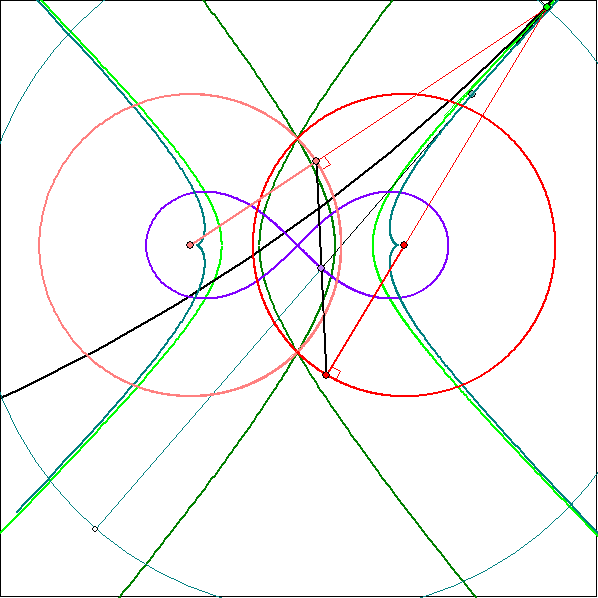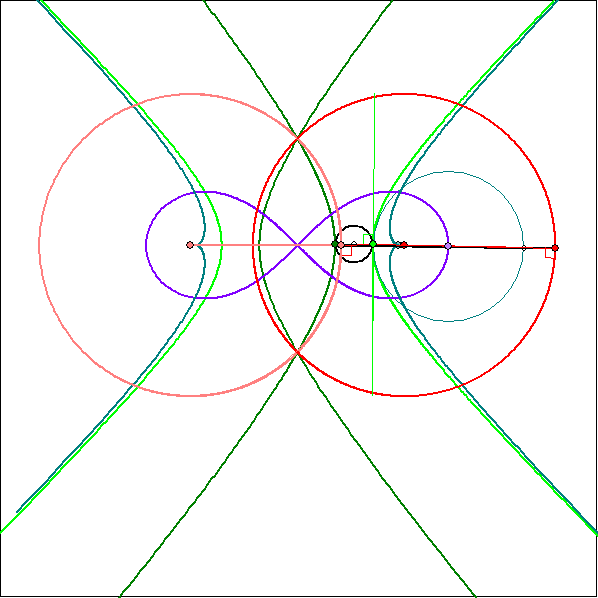
In der Animation werden Koppelkurven eines Zwillingskurbel-Getriebes mit den Arrmlängen 1 und mit
violett und ihre Evolute blaugrün dargestellt. Dabei bleibt die Stellung der Koppel
AB unverändert, nicht aber der Koppelpunkt Q, dessen Spur bei der Bewegung von A auf seinem Kreis
um M1 die jeweils gezeigte Koppelkurve ist. Q und der zugehörige Krümmungs-Mittelpunkt Q* auf der
Evolute ist durch eine Gerade g durch den Momentanpol D verbunden. Auf g liegt außerdem der weiß
gefüllt dargestellte Punkt S auf dem schwarzen 'Wendekreis', der wie die Sehne unverändert bleibt. Die
vier kollinearen Punkte Q, D, Q* und S stehen in einer besonderen Beziehung zueinander, die durch
den Satz von Euler-Savary ausgedrückt wird (Leonhard Euler 1707-1783; Félix Savary 1797-1841):

S ist das Bild der Spiegelung von Q* an dem Kreis um Q durch D.

Es gilt also . Dabei liegen Q* und S auf g stets auf der gleichen Seite von Q.

Falls die vier Punkte auf g die Reihenfolge D Q Q* S haben, ist
äquivalent mit , also mit ,
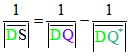was wiederum gleichwertig mit und ist.
Bei anderen Lagen der Punkte ergibt sich eine entsprechende Gleichung mit eventuell anderen
Vorzeichen. Wenn man auf g eine Orientierung festlegt und dazu eine signierte Streckenlänge
benutzt, die z. B. für Punkte X auf g rechts von D ein Plus-Zeichen setzt und für die links von D ein
Minus-Zeichen, dann gilt für alle Lagen der Punkte die Gleichung .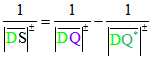

Diese Gleichung von Euler-Savary kann mit Hilfe von Bild 2 bis 7 in der Gleitschau nach der Animation
begründet werden: Hier ist die Geschwindigkeit des Koppelpunktes Q als violetter Pfeil
eingezeichnet. Im Momentanpol D ist der zugehörige Geschwindigkeitsvektor angeheftet, der die
Geschwindigkeit des Punktes D angibt, wenn er sich nicht auf der Geraden DQ verschieben würde,
sondern nur auf Grund der momentanen Drehung dieser Geraden um Q* bewegen würde. ist
die Komponente der Polwechselgeschwindigkeit senkrecht zu DQ, so dass und ein
rechtwinkliges Dreieck aufspannen, dessen zweite Kathete parallel zu DQ ist. (Der Thales-Kreis
über dem Vektor heißt 'Hartmann-Kreis' . Vergleiche dazu auch die Erklärungen auf der Seite
'Koppelgetriebe'.) Da der Momentanpol D momentanes Drehzentrum der Koppel ist, gilt für die
Winkelgeschwindigkeit der Koppel: . Für den Term auf der rechten Seite der
Gleichung von Euler-Savary ergibt sich nun mit dem violett markierten Winkel zwischen der
Geraden DQ und dem Vektor nach dem Strahlensatz: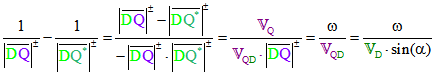
.
Der Wendekreis sei nun folgendermaßen definiert: Es ist der Kreis mit dem Durchmesser , der
den Vektor in D berührt, und zwar je nach Vorzeichen von rechts oder links davon. Dann ist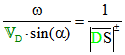
, und dieser Kreis hängt nur von der Stellung der Koppel ab, aber nicht von der
speziellen Wahl des Koppelpunktes.

In der Animation wird Q zunächst auf der Sehne AB hin- und herbewegt und anschließend auf der
Mittelsenkrechten von AB. Die auf die Animation in der Gleitschau folgenden Bilder 2 bis 7 dienen zur
Erklärung der Gleichung von Euler-Savary. Dabei wird außerdem deutlich, dass ein enger Zusammenhang
den Geschwindigkeits-Vektoren von A, B und Q besteht. Denn die Spitzen der Vektoren bilden stets ein
zum Dreieck ABQ ähnliches Dreieck. Wenn Q auf AB liegt, teilt die Spitze von die Strecke zwischen
den Spitzen der Geschwindigkeits-Vektoren von A und B im gleichen Verhältnis, wie Q die Strecke AB
teilt. Die Bilder 8 bis 22 sind Standbilder der Animation. Bild 11 und Bild 14 machen deutlich, wie man
den Wendekreis einfach konstruieren kann. Denn hier ist die Evolute zu jeweils einem Punkt geschrumpft,
nämlich zu M2 für Q = B bzw. M1 für Q = A. Nach dem Satz von Euler-Savary ist der Wendekreis
darum der Kreis durch folgende drei Punkte:

D,
Bild von M2 bei Spiegelung am Kreis um B durch D,
Bild von M1 bei Spiegelung am Kreis um A durch D.

Nachdem so zu einer Stellung der Koppel der Wendekreis konstruiert ist, ergibt sich S als Schnittpunkt des
Wendekreises mit der Geraden DQ und Q* als Bild von S bei Spiegelung an dem Kreis um Q durch D.

In Bild 4 und Bild 22 wurde die Kurve der Momentanpole hellgrün einzeichnet, die bei diesem
Zwillingskurbel-Getriebe eine Hyperbel ist. Sie berührt den Wendekreis stets im aktuellen Momentanpol.

Die Animation begründet den Begriff 'Wendekreis'. Hier wurden als Koppelpunkte die Punkte Q des
schwarzen Wendereises gewählt. Dann ist die Krümmung der zugehörigen Koppelkurve in Q gleich Null,
falls S ungleich D ist. Denn die Gerade g durch D und Q hat keinen weiteren gemeinsamen Punkt mit dem
Wendekreis. Darum stimmt S mit Q überein. Da S das Bild von Q* bei Spiegelung an dem Kreis um Q
durch D ist, muss Q* der unendlich ferne Punkt auf g sein. Folglich ist der Krümmungsradius unendlich
und die Krümmung Null. Diese Punkte mit der Krümmung Null können Scheitelpunkte oder Wendepunkte
der Koppelkurve sein. Zumeist sind sie Wendepunkte.

Die Bilder 1 bis 13 der Gleitschau sind Standbilder der Animation. In Bild 14 ist die Polare von M1
bezüglich des Kreises um A durch D blaugrün eingezeichnet, ebenso die Polare von M2 bezüglich des
Kreises um B durch D. Beide Geraden gehen durch den dunkelgrün gezeichneten Antipoden W von D
auf dem Wendekreis, der 'Wendepol' genannt wird. In Bild 15 ist zusätzlich die Polare eines Punktes Q*
zu einem Koppelpunkt Q bezüglich des Kreises um Q durch D eingezeichnet, die ebenfalls durch W
verläuft. Entsprechendes gilt für alle Krümmungs-Mittelpunkte Q*. Dies ermöglicht eine weitere Methode
zu Konstruktion von Q* bei gegebenem W, D und Q. Wenn nämlich die Polare von Q* durch W geht,
dann verläauft die Polare von W durch Q*, bezogen auf den gleichen Kreis um Q durch D. Der Punkt Q*
ergibt sich darum als Schnittpunkt der Polaren von W bezüglich des Kreises um Q durch D mit der
Geraden durch Q und D.

Die Animation zeigt die Veränderung des Wendekreises in Abhängigkeit von der Stellung der
Koppel beim Zwillingskurbel-Getriebe.

Die Animation zeigt die violette Koppelkurve bei einem Koppelgetriebe mit den Armlängen 1, dem
Abstand 2 der Mittelpunkte M1 und M2 und der Länge 1 der Sehne AB. In der ersten Periode der
Animation bildet der Koppelpunkt Q mit A und B ein gleichseitiges Dreieck. Die Koppelkurve besteht
aus zwei getrennten Teilen, die näherungsweise Abschnitte des Randes eines gleichseitigen Dreiecks mit
der Seitenlänge 2 bilden. Die Vervollständigung dieses Randes ergibt sich durch den entsprechenden
Koppelpunkt Q' auf der zu AB gehörenden Rückwärts-Sehne AB'. In der zweiten Periode wird Q auf
der Mittelsenkrechten von AB verschoben.

Bild 1 der auf die Animation folgenden Gleitschau zeigt die blaugrüne Evolute der Koppelkurve mit
einem Wendekreis. In den Bildern 2 bis 6 wurden die Wendekreise zu Stellungen der Koppel
gezeichnet, in denen der Koppelpunkt Q den Wendekreis trifft, so dass die Koppelkurve hier die
Krümmung Null hat und der zugehörige Punkt der Evolute im Unendlichen liegt. Diese Punkte sind
rot markiert. In den Bildern 7 bis 11 ist die hellgrüne Rastpol-Kurve der Momentanpole zusammen
mit der zugehörigen dunkelgrünen Gangpol-Kurve mit verschiedenen Berührpunkten dargestellt.
Bild 12 zeigt die blaue Enveloppe der Ko-Sehne BB', und Bild 13 die Koppelkurve für den Fall,
dass Q der Mittelpunkt von AB ist, zusammen mit der Momentanpol-Kurve und der Rauten-
Ergänzung der Sehnen.