Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Winkel
Geometrie 2 > Tetraeder
Trieder-Winkel beim Tetraeder
Wir betrachten auf dieser Seite die Relationen zwischen den Winkeln beim D-Trieder eines Tetraeders
ABCD , also für den Raum-Bereich, der von den drei Seiten-Ebenen durch den Punkt D begrenzt wird
und in dessen Innern das Tetraeder liegt. Wir bezeichnen die euklidischen Maße der Winkel BDC, CDA
und ADB mit![]() ,
, ![]() und
und ![]() . Es sind also Winkel zwischen Kanten. Die Maße der Winkel zwischen den
. Es sind also Winkel zwischen Kanten. Die Maße der Winkel zwischen den
Seiten-Flächen, die sich in den Kanten DA, DB und DC schneiden, bezeichnen wir mit ![]() ,
, ![]() und
und ![]() .
.
Die Zeilen der auf der Seite ' Monge' definierten Matrix H sind baryzentrische Quadrupel von u-Vektoren,
die euklidisch orthogonal zu den Seiten-Flächen sind. Zur Berechnung der Winkel zwischen den Seiten-
Flächen können wir diese vier Vektoren oder die vier Vektoren in Gegen-Richtung benutzen, um dadurch die
Unbestimmtheit zwischen Winkel und Neben-Winkel zu vermeiden. Die Maße der Winkel zwischen diesen
Vektoren stimmen mit den Maßen der Nebenwinkel der mit ![]() ,
, ![]() und
und ![]() gemessenen Winkel überein.
gemessenen Winkel überein.
Außer den Kanten- und Flächen-Winkeln betrachten wir das euklidische Maß ![]() des Raum-Winkels vom
des Raum-Winkels vom
D-Trieder. Aus der Oberfläche einer Kugel mit dem Radius 1 um D schneidet das D-Trieder zwei sphärische
Dreiecke heraus, die punktsymmetrisch zu D sind. Die Dreiecke werden von Bögen auf Kreisen mit dem
Zentrum D begrenzt. ![]() ist definiert als der Flächen-Inhalt jedes dieser Dreiecke. Der Inhalt der gesamten
ist definiert als der Flächen-Inhalt jedes dieser Dreiecke. Der Inhalt der gesamten
Oberfläche beträgt ![]() , wobei wir den hochgestellten Kreis als denFaktor
, wobei wir den hochgestellten Kreis als denFaktor ![]() ansehen.
ansehen.
In den Animationen benutzen wir ein gleichschenkliges Tetraeder ABCD, bei dem die Kanten DA, DB
und DC die Länge 1 haben. Dann liegen A, B und C also auf der Oberfläche der Kugel mit Radius 1 um D.
Der Fußpunkt des Lots von D auf die Fläche ABC ist der Mittelpunkt des Umkreises vom Dreieck ABC.
In den auf dieser Seite angegebenen Formeln bedeuten a, b und c die Seiten-Längen des Dreiecks ABC
im gleichschenkligen Tetraeder Tg. Man kann diese Formeln auf das D-Trieder eines beliebiges Tetraeders
Tb mit den Kanten-Längen a, b, c as, bs und cs anwenden, indem man a, b und c in den Formeln dieser
Seite ersetzt durch ![]() ,
, ![]() und
und ![]() . Dies sind die Längen der
. Dies sind die Längen der
Seiten in dem Dreieck mit Eckpunkten im Abstand 1 von D auf den Kanten-Geraden DA, DB und DC von Tb.
Diese Punkte haben bezüglich Tb die baryzentrischen Koordinaten ![]() ,
, ![]() und
und![]() . Wir nennen sie Eckpunkte des 'Einheits-Schnitts' des D-Trieders von Tb. Der Einheits-
. Wir nennen sie Eckpunkte des 'Einheits-Schnitts' des D-Trieders von Tb. Der Einheits-
Schnitt des A-Trieders von Tb hat Eckpunkte ![]() ,
, ![]() und
und ![]()
auf AD, AC und AB mit den Seiten-Längen ![]() ,
, ![]() und
und ![]() .
.
Zur Bestimmung der Nennern orientiert man sich an den Bezeichnungen der Kanten-Länge der Trieder,
also as, bs, cs bei D, as, b, c bei A, a, bs, c bei B und a, b, cs bei C. Im Zähler kommen die Buchstaben
'a', 'b' und 'c' alle drei vor, mit dem Zusatz 's' entweder zweimal oder keinmal.





Das erste Bild der Animation zeigt ein gleichschenkliges Tetraeder ABCD mit den Maßen der Kanten-
Winkel ![]() und der Flächen-Winkel
und der Flächen-Winkel ![]() .
. ![]() ,
, ![]() und
und![]() sind Maße von Winkel zwischen Vektoren, die senkrecht zu den Flächen verlaufen und am
sind Maße von Winkel zwischen Vektoren, die senkrecht zu den Flächen verlaufen und am
Mittelpunkt der Umkugel von ABCD angeheftet sind. A, B und C sind Punkte der Kugel K um D mit
dem Radius 1. Die Kreisbögen, welche diese Punkte verbinden, liegen auf den Schnitt-Kreisen von K mit
Seiten-Ebenen durch D. Die an A, B und C angehefteten Pfeile sind Tangenten-Vektoren dieser Kreise.
Sie schließen Winkel der Maße ![]() ,
, ![]() und
und ![]() ein.
ein.
Nach der Grund-Formel zur Berechnung des zu einem sphärischen Dreieck gehörigen Raum-Winkels ist![]() , also der Überschuss von der Summe der Maße der Innen-Winkel des
, also der Überschuss von der Summe der Maße der Innen-Winkel des
sphärischen und des ebenen Dreiecks mit den Eckpunkten A, B und C..
Die Maße von Kanten-Winkeln, Flächen-Winkeln und Raum-Winkel können in einem Satz, der dem Sinus-
Satz der Dreiecks-Geometrie entspricht, in einer Formel verbunden werden. Für ein gleichschenkliges
Tetraeder ABCD gilt :![]()
Für ein beliebiges Tetraeder gelten die ersten beiden Gleichheits-Zeichen immer, das dritte nur dann, wenn
man a, b und c in der oben angegebenen Weise ersetzt.
In der Animation wird ABCD um 360° gedreht. Anschließend werden a, b und c variiert.





Die Zeichnungen erklären die ersten beiden Gleichheits-Zeichen in dem oben angegebenen Sinus-Satz
für Trieder. Die rot gezeichnete Strecke verbindet den Eckpunkt A von ABCD mit dem Fußpunkt P
des Lots auf die Seite BCD; sie ist also die Raum-Höhe zu A. Von P aus wird das schwarze Lot auf die
Kante BD bzw. CD gefällt mit dem Fußpunkt Q bzw. R. Die schwarze Verbindungs-Gerade von Q bzw.
R mit A ist dann orthogonal zur Kante BD bzw. CD . Darum ist das Maß des Winkels PQA bzw. PRA
gleich ![]() bzw.
bzw. ![]() . Da AD die Länge 1 hat und das Dreieck ADQ rechtwinklig ist, hat AQ die Länge
. Da AD die Länge 1 hat und das Dreieck ADQ rechtwinklig ist, hat AQ die Länge
![]() und AP die Länge
und AP die Länge ![]() , da auch das Dreieck AQP rechtwinklig ist. Analog
, da auch das Dreieck AQP rechtwinklig ist. Analog
errechnet man ![]() . Daraus folgt
. Daraus folgt ![]() und analog mit der Höhe
und analog mit der Höhe ![]()
auch ![]() .
.
Zur Herleitung der Gültigkeit des dritten Gleichheits-Zeichens im oben angegebenen Sinus-Satz gibt es
bisher keinen geometrisch anschaulichen Weg. Es ist darum nötig zum Beweis auf Formeln der
sphärischen Trigonometrie (Trigonometrie auf der Kugel) zurückzugreifen. Wir gehen aus von den
Formeln, die Carl Mollweide (1774-1825) 1808 veröffentlicht hat. (Er transformierte bekannte
Formeln über ebene Dreiecke in Formeln über Kugel-Dreiecke.) Zur Formulierung benutzen wir die
oben verwandten Bezeichnungen der Winkel-Maße beim D-Trieder, lassen aber den Index D weg,
da die Formeln für jedes Tetraeder gelten. Nach Mollweide gilt :
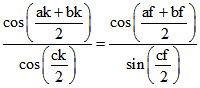 und
und 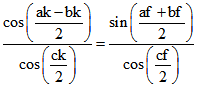
Hieraus folgt durch Subtraktion auf beiden Seiten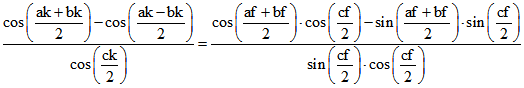
Wegen ![]() und
und ![]()
und ![]() und
und ![]() folgt
folgt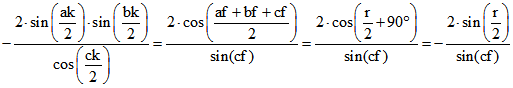
Es ist also 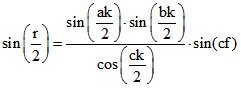 .
.
Da in unserem Tetraeder ABCD die Dreiecke ABD , BCD und CAD gleichschenklig sind, gilt![]() ,
, ![]() und
und ![]() , also
, also ![]() .
.
H sei die auf der Seite ' Monge' eingeführte Maß-Matrix für Ebenen, hier mit as = bs = c s = 1, und ![]()
der Flächeninhalt des Dreiecks ABC . Die Zeilen (und Spalten) von H sind baryzentrische Quadrupel von
u-Vektoren, die euklidisch orthogonal zu den Seiten von ABCD sind, und die Komponente ![]() ist das
ist das
Skalarprodukt der i-ten und der k-ten Zeile. Darum ist ![]() .
.
Man errechnet ![]() ,
,
![]()
und ![]()
und damit 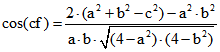 und
und ![]() , wobei
, wobei![]() das 12-fache Volumen von ABCD ist.
das 12-fache Volumen von ABCD ist.
Es folgt 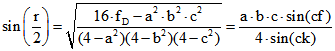 .
.
Untermenü