Es lebe die Geometrie!

Kugelkreis-Dreiseite mit rechtem Winkel

--> Geraden und Gewinde im dreidimensionalen projektiv-metrischen Raum I
https://www.vivat-geo.de/Pdf-Dateien/Geraden_und_Gewinde_I.pdf

Die Animation zeigt ein Dreiseit aus Kreisen a, b und c auf der Kugel mit dem Zentrum N(0 ; 0 ; 0)
und dem Radius 1. Der Nordpol liegt im Punkt (0 ; 0 ; 1), der Südpol im Punkt (0 ; 0; -1). Die
Kreise schneiden sich in jeweils zwei Punkten, von denen die Punkte A, B und C auf der Vorderseite
liegen und A*, B* und C* auf der Rückseite. Die Verbindungsgeraden AA*, BB* und CC* gehen
durch den gelb markierten Punkt Z. Die Kreise a und b schneiden sich bei jeder Lage von Z euklidisch
rechtwinklig in C und C*.

Die Tangentialebene im Nordpol wird durch eine gelbgraue Ellipse angedeutet, die den Einheitskreis
um den Nordpol darstellt. Die Geraden AA*, BB* und CC* schneiden diese Tangentialebene in den
Punkten A1, B1 und C1. Das Dreieck aus diesen Punkten ist nur dann euklidisch rechtwinklig, wenn
Z mit dem Südpol der Kugel zusammenfällt. Wenn Z auf der Geraden zwischen den Polen im Innern
der Kugel liegt, ist das Dreieck elliptisch rechtwinklig, wenn Z außerhalb der Kugel liegt, ist es
hyperbolisch rechtwinklig. Das Dreieck A1 B1 C1 ist oben links mit den Seitenmaßen angegeben,
die sich im Rahmen der elliptischen bzw. euklidischen bzw. hyperbolischen Geometrie ergeben.

Bei der Veränderung der Lage von Z bleiben die Punkte A1 und B1 und die euklidische Winkelgröße
des Winkels bei B unverändert, aber C1 wird verschoben, um zu sichern, dass der Winkel zwischen
den Kreisen b und a weiterhin die euklidische Größe 90° hat.

Oben rechts wird das Bild des Kugelkreis-Dreiseits a b c bei der stereographischen Projektion mit
dem Zentrum im Südpol und der Tangentialebene im Nordpol als Bildebene angegeben. Der Bildpunkt
eines Punktes P auf der Kugel ist also der Schnittpunkt der Tangentialebene im Nordpol mit der Geraden
durch P und den Südpol. Bei dieser stereographischen Zentral-Projektion werden Kugelkreise auf
Kreise in der Tangentialebene abgebildet, wobei die Schnittwinkel-Größen der Kreise auf der Kugel
mit denen der Bildkreise in der Ebene euklidisch übereinstimmen. Die Bildkreise von a und b schneiden
sich also euklidisch rechtwinklig. Die Seiten des Dreiecks der Bilder von A, B und C sind hier nach außen
gewölbt, wenn Z zwischen dem Nord- und Südpol liegt, und nach innen, wenn sich Z außerhalb der
Kugel befindet. Darum ist die euklidische Innenwinkel-Summe des Kreis-Dreiseits im elliptischen Fall
größer als 180° und im hyperbolischen kleiner als 180°. Für Z im Südpol werden die Kreise zu Geraden
und die euklidische Winkelsumme gleich 180°.

Während die Abwandlung der Kugelkreis-Geometrie oben links sich am Beltrami-Klein-Modell der
ebenen hyperbolischen Geometrie orientiert, entspricht das Bild oben rechts dem Poincaré-Modell
der ebenen hyperbolischen Geometrie. Wir nennen diese Abwandlungen der Kugelkreis-Geometrie
auch dann 'Klein-Modell' bzw. 'Poincaré-Modell' im Gegensatz zum üblichen Sprachgebrauch, wenn
Z im Innern oder auf der Kugelfläche liegt und in der dargestellte Geometrie darum Winkel und
Seitenlängen mit einem elliptischen bzw. euklidischen Maß gemessen werden.

Die Werte für Größen von Winkeln stimmen im Klein- und im Poincaré-Modell mit den euklidischen
Größen der entsprechenden Winkel zwischen Kugelkreisen überein, auch dann, wenn Z nicht auf der
Kugelfläche liegt. Die Maß-Bestimmung für Seitenlängen ist jedoch komplizierter. Das zeigt sich schon
daran, dass einem Punkt im Klein-Modell ein Punkte-Paar im Poincaré-Modell entspricht, weil bei der
stereographischen Projektion z. B. A und A* in verschiedene Punkte abgebildet werden, während bei
der Projektion mit dem Zentrum Z sowohl A als auch A* in A1 abgebildet werden. Unter einem 'Punkt'
im Poincare-Modell muss man darum ein Punkte-Paar verstehen. Entsprechend bezeichnen wir das
Punkte-Paar (A , A*) auch als 'Punkt' (in Anführungsstrichen und violett). Bei vorgegebenem Punkt Z
kommt man dadurch zu einem weiteren Modell der elliptischen, euklidischen oder hyperbolischen
Geometrie durch folgende Definition: Ein 'Punkt' dieses Modells ist ein Paar zweier verschiedener
Punkte auf der Kugelfläche, deren Verbindungsgerade durch Z geht. Eine 'Gerade' dieses Modells ist
ein Kreis auf der Kugelfläche, der in einer Ebene durch Z liegt. Wir nennen dieses Modell 'Kugelkreis-
Modell zu Z'. Winkel werden darin euklidisch gemessen. Die Messung des Abstands zweier 'Punkte'
wird im Folgenden erklärt. Um die 'Geraden' und 'Punkte' des Kugelkreis-Modells von den gewöhnlichen
Punkten und Geraden zu unterscheiden, benutzen wir im Folgenden die violette Farbe für Kugelkreise in
einer Ebene durch Z. Wir verwenden also z. B. die Bezeichnungen Z-'Mittelsenkrechte', Z-'Seitenhalbierende',
Z-'Winkelhalbierende' und Z-'Höhe':

Die Maßbestimmung der Abstände ist für drei Lagen des Punktes Z besonders einfach, nämlich für
Z im Mittelpunkt N der Kugel, für Z im Südpol und für Z im 'unendlich fernen' Punkt U auf der z-Achse
durch Nord- und Südpol. (U ist dadurch charakterisiert, dass er genau auf den Geraden im Raum liegt,
die parallel zur z-Achse sind. )

Wenn Z im Mittelpunkt der Kugel liegt, ist jeder Kreise, die von einer Ebenen durch Z aus der
Kugelfläche ausgeschnitten wird, ein Großkreis vom Radius 1. Der Abstand zweier 'Punkte'
(A;A*) und (B;B*) auf diesem Kreis wird dann durch das Minimum des Betrags der Winkelgrößen
ANB und ANB* definiert. Dieser Abstands-Wert wird auch für das Klein-Modell und das Poincare-
Modell übernommen. Wenn A bzw. B den Ortsvektor bzw.
hat, dann ist . Für ein rechtwinkliges elliptisches
Dreieck mit Eckpunkten (A;A*), (B;B*) und (C;C*) mit rechtem Winkel bei C ist dann
,
da auf Grund der Lagrange-Identität gilt:


Im Fall, dass Z im Südpol liegt, fallen die Punkte A*, B* und C* mit dem Südpol zusammen. A1 ,
B1 und C1 sind dann die Bilder von A, B und C bei der stereographischen Projektion und bilden
ein euklidisch rechtwinkliges Dreieck. Die Seiten-Maßzahlen im Bild oben links sind dann die
euklidischen Seitenlängen und in dem rechtwinklige Dreieck A1 B1 C1 gilt der Satz von Pythagoras.

Wenn Z der unendlich ferne Punkt U auf der Geraden g durch Nord- und Südpol ist, sind die
Geraden durch Z die Parallelen zur z-Achse und die Ebenen durch Z stehen senkrecht auf der
xy-Ebene. Das Problem der Punktepaare kann man hier dadurch mildern, das man bei den 'Punkten'
nur die Komponente auf der oberen Halbkugel ohne den Äquator betrachtet und als 'Geraden' die
Halbkreise der oberen Halbkugel ansieht, die auf dem Äquator senkrecht stehen. Die Größe des
Winkel zwischen zwei 'Geraden' dieser hyperbolischen Geometrie wird durch das euklidische
Winkelmaß der Halbkreise definiert. Zur Definition des hyperbolischen Abstand zwischen zwei
Punkten A und B betrachtet man die Bilder A2 und B2 dieser Punkte bei senkrechter Projektion
auf die x-y-Ebene. Die Gerade durch A2 und B2 schneidet den Einheitskreis um N in dieser Ebene in
zwei Punkten D und E . Der hyperbolische Abstand von A und B ist dann die Hälfte vom natürlichen
Logarithmus des Doppelverhältnisses

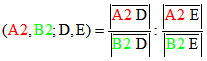
Dabei ist z. B. die euklidische Länge der durch A2 und D bestimmten Strecke.
Man kann zeigen, dass dann gilt: .
(Siehe z. B. http://www.vivat-geo.de/Pdf-Dateien/Hyperbolische_Geometrie.pdf S.80)
Dies zeigt die Bedeutung einer Quadratform, die dadurch entsteht, dass man beim inneren Produkt
zweier Vektoren und ein Plus-Zeichen in ein Minus-Zeichen umwandelt.
Statt des Punktes benutzen wir dafür einen Stern:
Zwei hyperbolische 'Geraden', deren Ebenen die x-y-Ebene in den Geraden mit den Gleichungen
und schneiden, sind genau dann orthogonal, wenn
ist. Für die 'Geraden' durch A und C bzw. B und C bedeutet dies, dass
gilt. Die linke Seite dieser Gleichung
kann mit einer Variation der Lagrange-Gleichung zu


umgewandelt werden, woraus dann folgt.

Wenn Z weder N noch U und auch nicht der Südpol ist, gelingt einen Rückführung auf den Fall
Z = N für Punkte Z zwischen Nord und Südpol und auf den Fall Z = U für Z außerhalb der Kugel.
Sei Z der Punkt (0;0;z). Für z zwischen -1 und 0 sei dazu der Punkt M mit den Koordinaten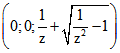
betrachtet; für z<-1 sei M der Punkt . Dann bildet die
Spiegelung im ersten Fall Z in N ab und im zweiten Fall Z in U. Durch werden die
zugehörigen 'Punkte' und 'Geraden' ebenfalls abgebildet. Man übernimmt dann die Maße
für 'Punkte' -Paare und 'Geraden' -Paare zu Z von ihren Bilden zu N bzw. U.

Die Polar-Ebene zu Z ist für Z = U die x-y-Ebene. Sie spielt für die Abstandsmaß-Bestimmung
auch dann eine Rolle, wenn Z nicht gleich U ist. Sie ist zeitweise durch einen zweiten gelbgrauen
Einheitskreis unterhalb des gelbgrauen Kreises der Tangentialebene des Nordpols in der Animation
angedeutet. Der Abstand des Kugelmittelpunktes N von dieser Polarebene ist der Kehrwert des
euklidischen Abstands N von Z. Die Schnittpunkte A2 , B2 und C2 der Geraden AA*, BB* und
CC* mit der Polarebene von Z sind in der Animation eingezeichnet. Wenn Z zwischen Südpol
und N liegt, ist der Abstand z.B. der Punkte' (A , A*) und (B , B*) die euklidische Winkelgröße
des Winkels A2 M B2. Der 'Maßpunkt' M liegt in diesem Fall auf den drei Kugelflächen mit den
Mittelpunkten A2 , B2 und C2 , welche die Kugelfläche um N senkrecht schneiden. In einem Teil
der Animation ist M als großer orangefarbiger Punkt eingezeichnet. Im Sonderfall Z = N ist die
zugehörige Polarebene die 'unendlich ferne' Ebene mit Punkten A2 , B2 und C2 , die man sich als
die Mengen von Geraden parallel zu den Geraden AA*, BB* und CC* vorstellen kann.

Im Fall, dass Z außerhalb der Kugel liegt, schneidet die Polarebene von Z die Kugel. Die Gerade
durch A2 und B2 hat dann mit der Kugel zwei Punkten D und E gemeinsam und der Abstand der '
Punkte' (A , A*) und (B , B*) wird mit Hilfe von A2 und B2 wie im Fall Z = U bestimmt.

Die beiden Bilder der folgenden Gleitschau sollen den Zusammenhang zwischen der Spiegelung
an M und den Schnittpunkten der Geraden durch Z mit der Polarebene klar machen. Dabei wird
der Schnitts der Kugel mit einer Ebene durch die z-Achse betrachtet.

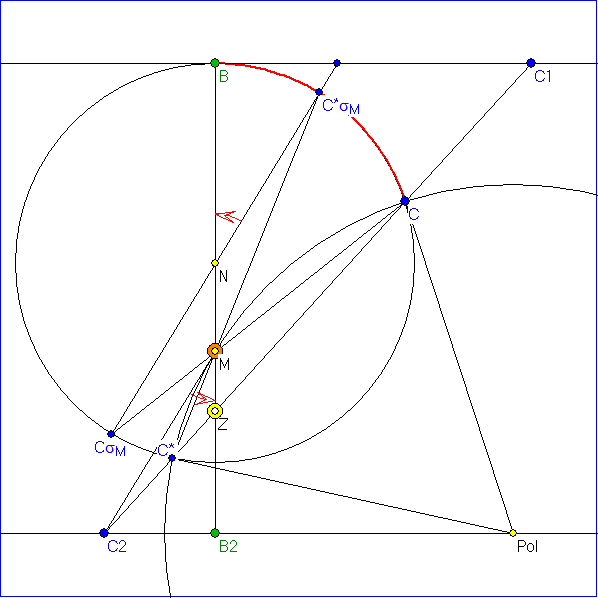
Die Zeichnungen der Gleitschau stellen die Abstands-Maßbestimmung an Hand einer Ebene durch
Z, B und C dar, wobei B in den Nordpol versetzt wurde. Im ersten Bild liegt Z zwischen Nord-
und Südpol. M ist der Schnittpunkt der z-Achse NB mit dem Kreis, der den Einheitskreis um
N in C und C* senkrecht schneidet. Der Mittelpunkt dieses Kreises ist der Pol der Geraden CC*
bezüglich des Einheitkreises. Die Lotgerade zur z-Achse durch diesen Pol liegt in der Polarebene
von Z. Die Gerade CC* wird durch in eine Gerade durch N abgebildet. Die Größe des roten
Winkels bei N gibt die Länge des roten Bogens im Rahmen der durch Z bestimmten elliptischen
Geometrie an. Dieser Winkel ist gleich groß wie der ebenfalls rot markierte Winkel ZMC2.

In der zweiten Zeichnung liegt Z außerhalb der Kugel. Die Gerade durch die Berührpunkte der
Tangenten von Z an den Einheitkreis um N = B3 isr die Polare von Z bezüglich dieses Kreises
und liegt in der Polarebene von Z bezüglich der Kugel. M ist der Schnittpunkt der beiden
Geraden, die diese Berührpunkte mit den Schnittpunkten des Einheitskreises und der x-Achse
verbinden. Die Gerade CC* wird durch in eine Parallele zur z-Achse durch abgebildet,
die die x-Achse in C3 schneidet. C3 liegt auf der Geraden durch M und C2. In der zu Z gehörigen
hyperbolischen Geometrie hat der rote Bogen BC die gleiche Länge wie der Bogen in der
zu U gehörigen hyperbolischen Geometrie, bei der die Parallelen der Geraden ZN zum Vermessen
der Bögen benutzt werden und die Doppelverhältnisse sich auf die Punkte der xy-Ebene durch N
beziehen.

Wenn und die Koordinaten von B2 und C2 sind, dann ist für
Z im Innern der Kugel der Cosinus-Wert des Abstands der Punkte' (B , B*) und (C;C*)
gleich 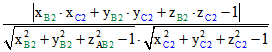, falls Z ungleich N ist,
und gleich 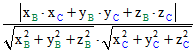im Fall Z = N, wobei der Nenner hier gleich 1 ist.
Wenn Z außerhalb der Kugel liegt, ist der Cosinus-hyperbolicus-Wert des Abstands der Punkte'
(B , B*) und (C;C*) gleich