Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Würfel-Kachelung
Geometrie 1 > Großkreis-Kachelungen
Großkreis-Kachelung, die durch Spiegelungen an den Seiten aus
einem Kreis-Dreieck mit Winkeln 90°, 60° und 45° erzeugt wird
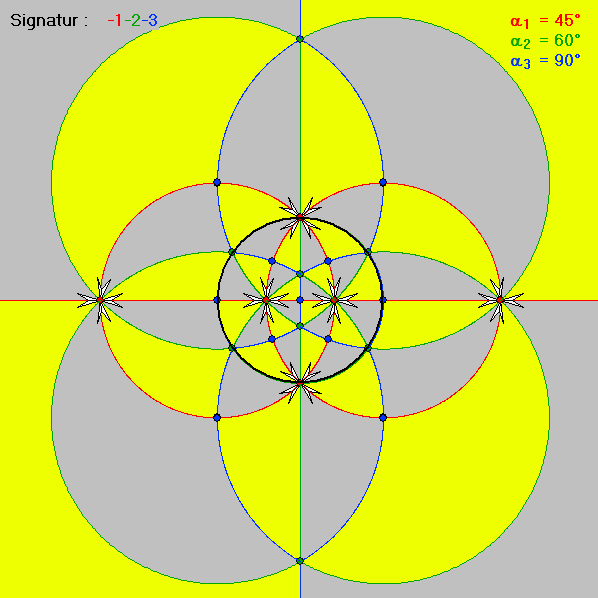





Das Ausgangsdreieck dieser Kachelung mit den Innenwinkeln 90°, 60° und 45° hat im Poincaré-
Modell im Bild 1 die Eckpunkte ![]() ,
, ![]() und
und ![]() . Der Mittelpunkt
. Der Mittelpunkt
des Kreise zur Seite 2 hat die Koordinaten ![]() . In Bild 2 sind die Höhen auf der Seite 2
. In Bild 2 sind die Höhen auf der Seite 2
zusätzlich eingezeichnet worden. Wir nennen diese Kachelung 'Würfel-Kachelung', da im Kugel-Modell
die Verbindung der grünen Eckpunkte mit der Nummer 2 einen Würfel ergibt, wie Bild 3.4 und 5
zeigen. Die blauen Eckpunkte liegen hier über den Kanten-Mitten des Würfels und die roten über den
Flächen-Mitten. Nach Bild 6 führt die Verbindung der roten Eckpunkte zu einem Oktaeder mit den
blauen bzw. grünen Punkten über den Mitten der Kanten bzw. Flächen. Die Verbindung der blauen
Punkte in Bild 7 führt dagegen nicht zu einem platonischen Körper, sondern zu einem archimedischen,
nämlich einem Kuboktaeder. Diesen kann man sich dadurch erzeugt denken, dass man bei einem
Würfel mit Eckpunkten über den grünen Punkten die Ecken bis zur Mitte der Kanten abschneidet.
Alternativ kann man bei einem Oktaeder mit Eckpunkten über den roten Punkten die Ecken bis zur
Mitte der Kanten abschneiden. Bild 8 macht deutlich, dass die Kanten des Kuboktaeders den
magentaroten Höhen auf den Seiten 2 folgen, so dass die Lotfußpunkte über den Kanten-Mitten
liegen. Bild 9 zeigt das Klein-Modell der Würfel-Kachelung zusammen mit den Höhen. Zwei im
Sinne der elliptischen Geometrie orthogonalen Geraden sind nur dann auch euklidisch orthogonal,
wenn mindestens eine der beiden Geraden durch den blauen Nordpol im Zentrum des schwarzen
Kreises C geht.





Die Animation zeigt die Entstehung der Würfel-Kachelung aus einem Ausgangs-Dreieck mit
den Eckpunkten ![]() ,
, ![]() und
und ![]() . Die Berechnung dieser
. Die Berechnung dieser
Koordinaten ergibt sich aus den Innenwinkel ![]() in folgender Weise:
in folgender Weise:
Für eine Dreieck mit Großkreisbögen gilt nach dem Winkel-Kosinussatz der sphärischen
Trigonometrie ![]() . Dabei sind
. Dabei sind ![]() die
die
Innenwinkel der Dreiecks und c die Länge des Seiten-Bogens, der dem Winkel ![]() gegenüber
gegenüber
liegt, vorausgesetzt dass die Kugel den Radius 1 hat. Mit ![]() folgt daraus
folgt daraus
![]() . Mit den Formeln, die sich durch zyklische Permutation der Innenwinkel
. Mit den Formeln, die sich durch zyklische Permutation der Innenwinkel
ergeben, erhält man entsprechend ![]() und
und ![]() .
.
Wenn der Eckpunkt A im Nordpol und B und C wie in der Animation in Koordinatenebenen
liegen, berechnet man für die Bilder von B und C bei der gnomischen Projektion:![]() und
und 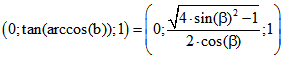 .
.
Dies sind also neben dem Nordpol die Eckpunkt des Ausgangs-Dreiecks im Klein-Modell. Durch
Einsetzung in die Formel 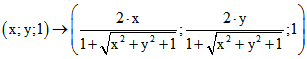 für den Übergang zum
für den Übergang zum
Poincare-Modell ergeben sich die Punkte 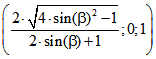 und
und 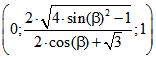 .
.










Diese beiden Animationen zeigen, dass die Teil-Kachelung im Poincaré-Modell im Innern
bzw. im Äußeren des schwarzen Kreises C vom Radius 2 ausreicht, damit die zugeordnete
Kachelung im Klein-Modell die Ebene vollständig ausfüllt.
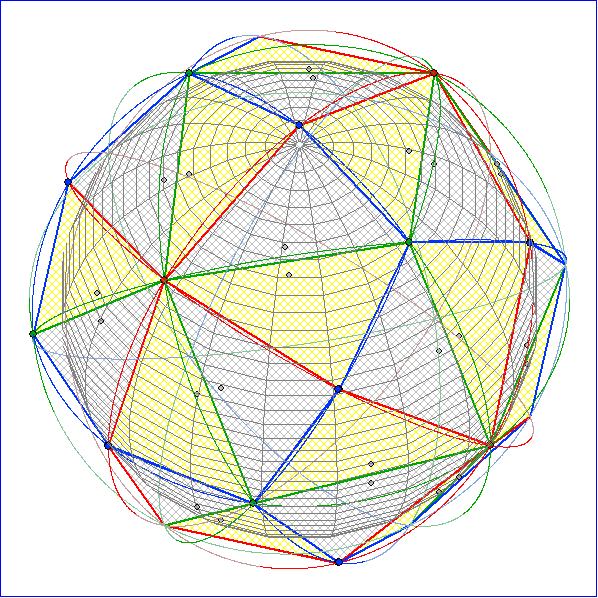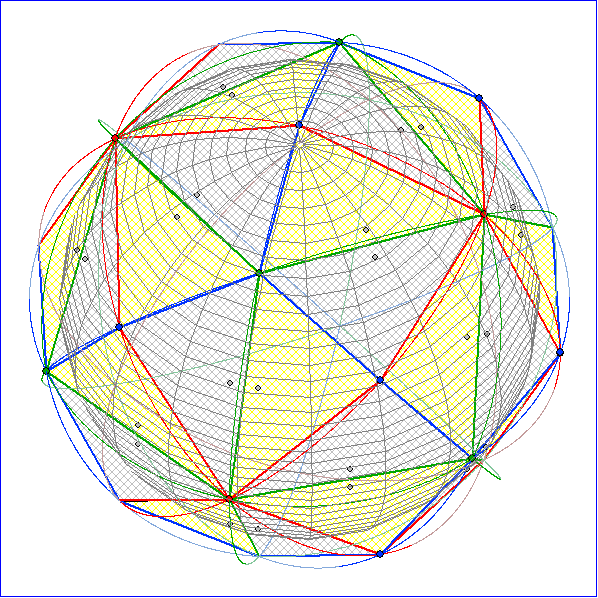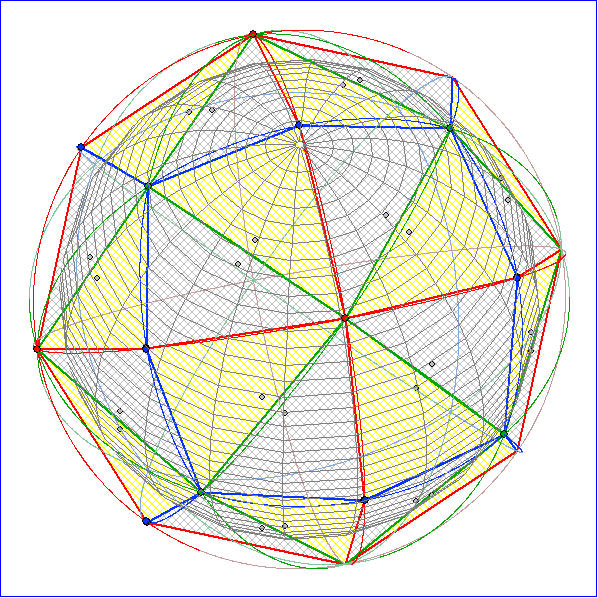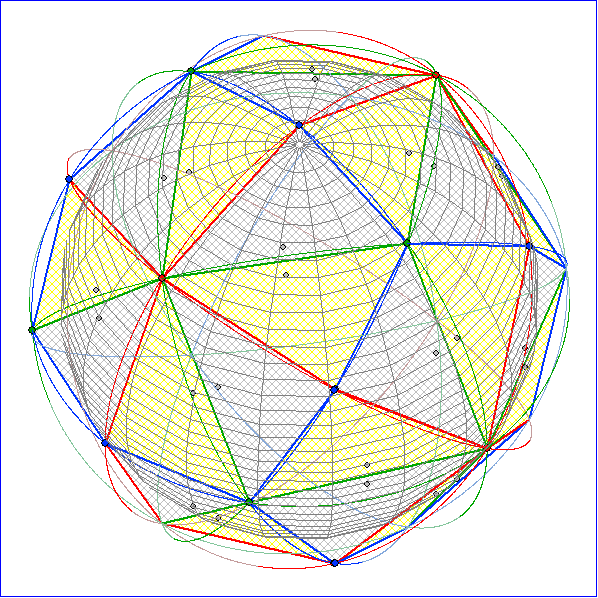





Die Animation zeigt das Polyeder der Würfel-Kachelung und in der Gleitschau einzelne Bilder
analog zur vorherigen Seite über die Tetraeder-Kachelung.
Aus der oben angegebenen Berechnung der Eckpunkte der Ausgangs-Kachel im Klein-Modell
folgt, dass die entsprechenden Eckpunkte A, B und C im Kugel-Modell mit der Abkürzung![]() folgende Koordinaten haben:
folgende Koordinaten haben:![]() ,
, ![]() und
und ![]() .
.
Hierbei ist ![]() die euklidische Größe des Winkels beim roten Punkt B im Poincaré oder Kugel-Modell,
die euklidische Größe des Winkels beim roten Punkt B im Poincaré oder Kugel-Modell,
wird also zwischen Kreisbögen gemessen. Für die Tetraeder-Kachelung ist also ![]() , für die
, für die
Würfel-Kachelung 45° und für die Ikosaeder-Kachelung 36°.
Die rote, grüne bzw. blaue Seite hat die Länge![]() ,
, 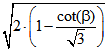 bzw.
bzw. ![]() .
.
Für die Größe des Winkels zwischen der roten und der blauen Seite ergibt sich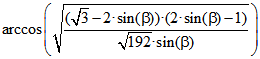 .
.
Der Radius der Inkugel beträgt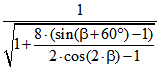
Untermenü