Es lebe die Geometrie!

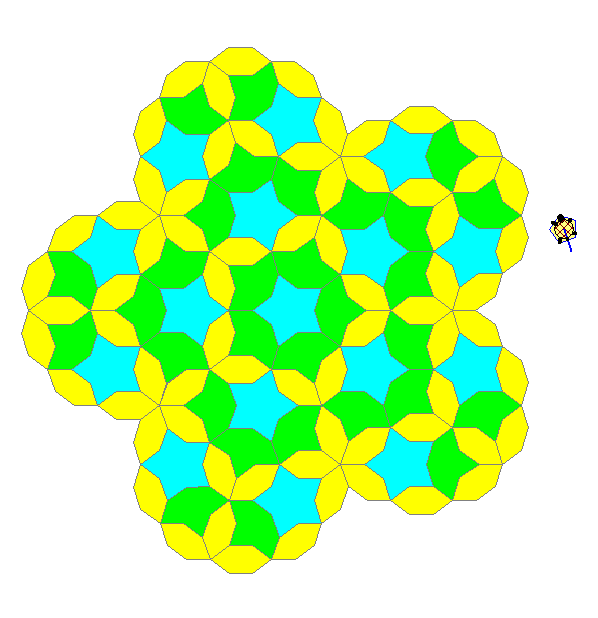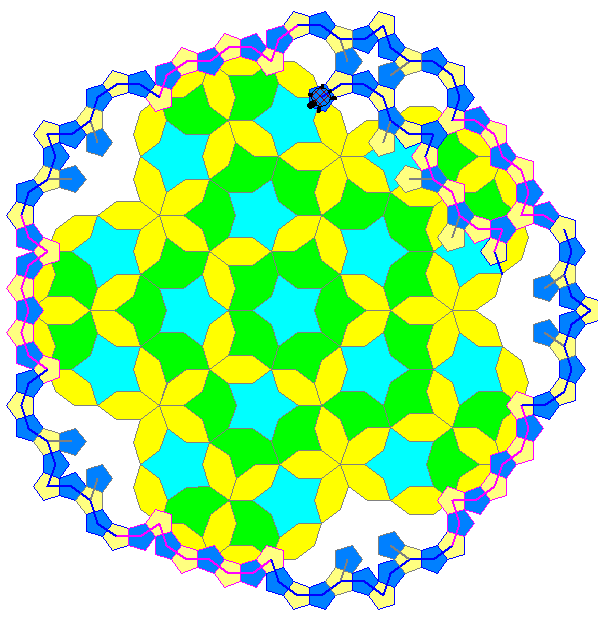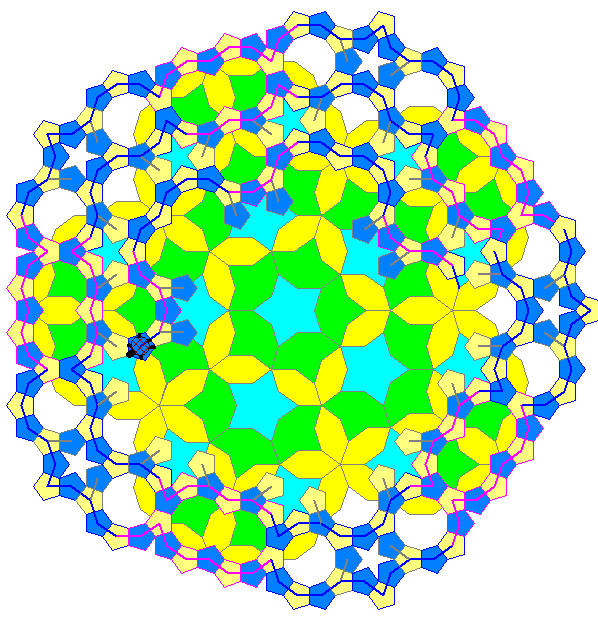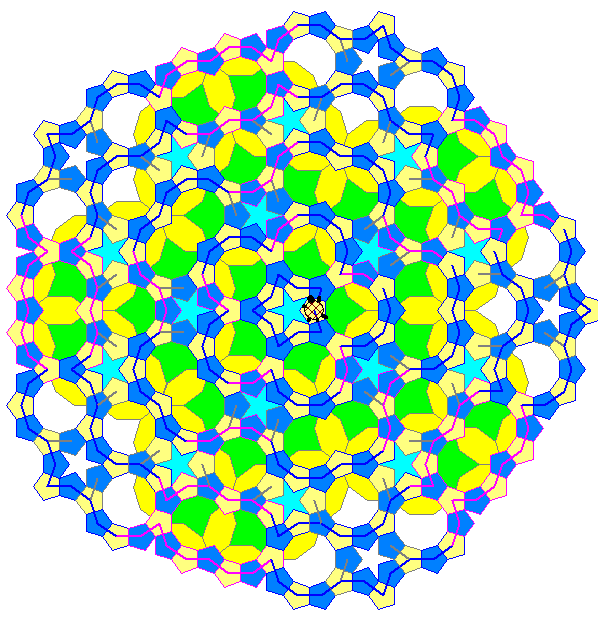
Keplers Kränze

Johannes Kepler (1571 bis 1630) hat in seinem Buch 'Weltharmonik' (1619) neben der Darstellung des
3. keplerschen Gesetzes über die Planetenbahnen auch Kachelungen der euklidischen Ebene untersucht. Es
ging ihm unter Anderem um die Frage, wie man die Ebene durch Aneinanderlegen von regulären Fünfecken
möglichst regelmäßig ausfüllen kann. Dabei ist er auf eine Kachelung mit regulären Fünfecken, Zehnecken
und 5-Sternen, sowie einem Sechzehneck mit gleich langen Seiten und zwei Symmetrieachsen gestoßen.

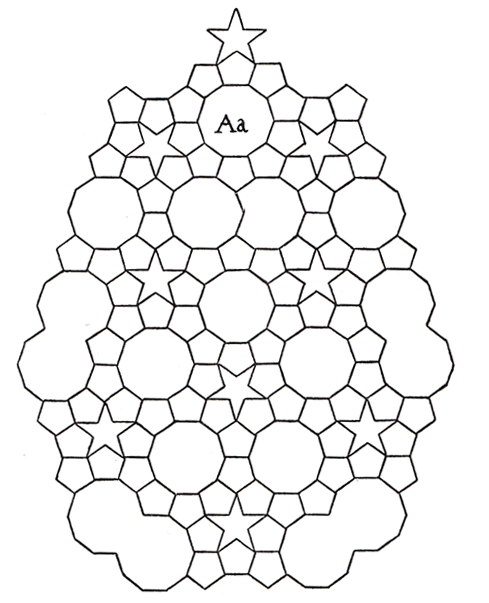
Kepler schreibt zu diesem Bild in der 'Weltharmonik' (Übersetzung aus dem Lateinischen nach Max Caspar)
nach einer Betrachtung über reguläre Fünfecken und 5-Sternen:

Das Reich dieser Sekte ist ungesellig; sie zieht eine kleine Anzahl der Ihrigen zusammen und verschanzt sich
dann sofort. Eine andere Verbindung dieser beiden Formen zeigt die Figur Aa. Will man diese überallhin
fortsetzen, so muss man gewisse Ungetüme heranziehen, nämlich die Verbindung zweier Zehnecke, von denen
je zwei Seiten weggenommen sind. Bei der unendlichen Fortsetzung behält das Gefüge seine fünfeckige
Gliederung. Auf dem ersten, innersten Fünfeckskranz sitzen fünf Zehnecke, ohne Ungetüm dazwischen. Auf
dem zweiten weiteren Kranz sitzt auf jeder Fünfeckseite allemal zwischen zwei Zehnecken ein Paar gekoppelter
Zehnecke. Auf dem dritten Kranz sitzen in den Ecken Paare gekoppelter Zehnecke, und zwischen zwei solchen
Paaren liegt je ein einfaches Zehneck. Auf dem vierten Kranz sitzen in den Ecken wieder einfache Zehnecke,
und zwischen zwei dieser Zehnecke sitzen auf den Seiten je zwei Zehnecke in gleichen Abständen voneinander.
Auf dem fünften Kranz sitzen in den Ecken Sterne mit ihren äußersten Zacken; auf den Seiten sitzen je zwei
einfache Zehnecke und zwischen diesen zwei Zehneckskoppeln. So trägt fortlaufend jede Fünfecksform etwas
Neues in sich. Die Struktur ist höchst mühsam und kunstreich,wie aus Figur Aa zu sehen ist.

Die Animation besteht aus zwei Teilen. Im ersten Teil legt eine Schildkröte auf sieben geschlossenen Wegen
mit einem gemeinsamen Zentrum reguläre Fünfeck-Kacheln so aneinander, dass aufeinander folgende Kacheln
eine Seite gemeinsam haben und unterwegs kein Punkt zweimal durchlaufen wird. Wir nennen diese sieben
Kachel-Folgen 'Kränze'. Im zweiten Teil der Animation werden diese Kränze durch unterwegs zusätzlich
abgelegte Fünfeck-Kacheln so verbunden, dass als Leerstellen 5-Sterne, reguläre Zehnecke und Sechzehnecke
übrig bleiben.

Im Anschluss an die Animation zeigt die Gleitschau Standbilder daraus. Das letzte (15.) Bild der Gleitschau
soll die Systematik des Anlegens verdeutlichen. Dabei wurden nummerierte Strecken eingezeichnet. die
folgende Bedeutung haben:

Den Weg der Schildkröte zeigt der dick blau oder rot gezeichnete Streckenzug an, der die Mitten der
regulären Fünfecke als Eckpunkte hat. Die Größe der Richtungwinkel der zugehörigen Strecken gegenüber
der Richtung nach rechts ist stets ein ganzahliges Vielfaches von 36°. Wir beschreiben diese Richtung
mit Hilfe der ganzen Zahl k zwischen 0 und 9. Es zeigt sich, dass bei den Kepler-Kränzen viele Strecken mit
gleicher Richtungswinkel-Zahl kollinear sind, also gemeinsam auf einer Geraden liegen. Das gilt auch für die
durch fette Zahlen blau oder grau markierten Strahlen, die von den Seiten-Mitten des innersten 5-Stern-
Kranzes ausgehen. Diese Strahlen haben die Richtungswinkel mit ganzzahligem i. Neben
diesen Strahlen, die nur Mitten von Strecken mit dem gleichen Richtungswinkel treffen, sind beim Richtungs=
winkel 56° auch solche eingezeichnet, bei denen zwei verschiedene Richtungswinkel vorkommen. Die Folge
der dabei getroffenen Richtungswinkel-Zahlen ist dann stets periodisch mit der Periode 3, zum Beispiel
353353353... oder 553553553....

Die Folgen ganzer Zahlen, die oben links im Bild zu sehen sind, geben die Richtungswinkel-Zahlen für
einen 72°-Sektor des Wegs der Schildkröte an. Für den n-ten Kranz ist dabei die i-te Zahl durch
folgende Funktion ri(n ; i) gegeben, wobei die Verknüpfungen div und mod für ganze Zahlen i und m
durch die Gleichung bestimmt sind mit .

function ri(n,i:integer):integer;
begin
if i=0 then ri:=3
else if i<=2*n+2 then
begin
if i mod 2=1 then if (n-(i-1) div 2) mod 3=0 then ri:=2 else ri:=4
else if (i div 2) mod 3 = 1 then ri:=5 else ri:=3
end
else
begin
if i mod 2=1 then if (n-(i-1) div 2) mod 3=0 then ri:=6 else ri:=4
else if ((4*n-i) div 2) mod 3 = 1 then ri:=3 else ri:=5
end;
end;

Die Drehung um das Zentrum der Kränze mit dem Drehwinkel 72° bringt alle Kränze mit sich zur Deckung.
Da die Richtungen in dem oben betrachteten Sektor mit der Nummer Null durch ri gegeben sind, werden sie
in den folgenden Sektoren mit der Nummer m durch beschrieben.

Bemerkenswert ist, dass sich beim Weg der Schildkröte gerade und ungerade Richtungszahlen abwechseln,
was sich auch im Wechsel zwischen blauer und gelber Kachel ausdrückt. Auch wenn die Kränze durch
Kacheln verbunden sind, haben nie Kacheln mit gemeinsamer Seite die gleiche Farbe.

Diese Gleitschau zeigt eine weitere Regelmäßigkeit der Kepler-Kränze (nach Dessecker), auf die zum
Beispiel auch in dem Buch 'Tilings and Pattern' von Branko Grünbaum und G.C. Shephard hingewisen
wird (W.H. Freeman 1989). Die Strahlen mit den grauen und blauen Richtungs-Zahlen begrenzen
zehn Sektoren mit dem Öffnungswinkel 36°, von denen sich die fünf gelb unterlegten im innersten Kranz
überschneiden und die orange unterlegten die verbleibenden Lücken füllen. Man kann diese Sektoren mit
Rauten ausfüllen, die aus der Vereinigungsmenge der Kränze kongruente Teile herausschneiden, die wir
'Kepler-Rauten' nennen. Innerhalb eines Sektors gehen diese Rauten-Kacheln sogar durch Translationen
ineinander über. Dies bedeutet nicht, dass die Kepler-Kachelung aus Fünfecken, 5-Sternen, Zehnecken
und 'Ungetümen' insgesamt periodisch ist, denn die Situation am Zentrum ist singulär; man könnte sie aber
'teilperiodisch' nennen.

Die Gleitschau zeigt den dick blau gezeichneten Fünfeck-Pfad zu einer Kepler-Raute und ihre Füllung
mit weiteren regulären Fünfecken. Das erste Bild gibt einen Umlauf der Schildkröte um die Raute mit
den dabei abgelegten Fünfecken und mit der Folge der Richtungs-Zahlen an. Die Differenzen
aufeinanderfolgender Richtungs-Zahlen bleiben bei Drehungen der Raute um ganzzahlige Vielfache
von 36° unverändert. An ihnen ist auch leichter erkennbar, dass die Spur der Schildkröte die gleich
Symmetrie zu den Diagonalen hat wie die Raute.

Im ersten Bild wurden zusätzlich Fünfeck-Zentren senkrecht auf die Diagonalen projiziert.
Dabei zeigt sich eine Regelmäßigkeit in den Abständen. Diese haben folgenden Grund:

sei der Verschiebungsvektor von einem Fünfeck-Zentrum zum nächsten mit der Richtungszahl k.
Wenn die Länge dieser Vektoren eine Einheit beträgt, gilt in komplexer Schreibweise
. Die beiden Vektor-Komponenten können mit Hilfe der goldenen
Zahlen und und der goldenen Quadratwurzeln und
ausgedrückt werden. Für jede ganze (auch negative) Zahl n gilt dabei ,
woraus wegen und folgt: , und .
Es ist ,
,
,
,

und es gilt .
Die Abstände zwischen benachbarten weiß gefüllten Punkten auf der horizontalen Rauten-Diagonale
sind darum die Hälfte von g, 1 oder G. Der Abstand des ersten dieser Punkte zum letzten beträgt
. Auf der vertikalen Rauten-Diagonalen springen aufeinanderfolgende
Punkte hin und her mit den Sprungweiten 0, und . Dabei ist
. Die Länge der senkrechten Projektion der Rautenseite auf die
vertikale Diagonale ist . Für die Seitenlänge der Raute ergibt sich
daraus .

Der Richtungswinkel der Rautenseite unten links ist -18°. Denn die Folge 9810901890 der Richtungs-Zahlen
ergibt einen Verschiebungs-Vektor mit zwei Summanden zum Richtungswinkel -18°.

Die Seitenlänge der regulären Fünfecke beträgt .

Das zweite Bild der Gleitschau zeigt die Füllung der Raute nach Kepler und weiß gefüllte Punkte auf der
horizontalen Diagonalen. Wir denken uns diese Punkte von 1 bis 13 nummeriert. Es treten dann folgende
Abstände auf:





, also .

Im dritten Bild der Gleitschau werden auch die regelmäßigen Zehnecke und die 'Ungetüme' mit Fünfecken so
gefüllt, dass die Achsensymmetrie möglichst erhalten bleibt. Diese ist jedoch beim Ungetüm hinsichtlich
der Symmetrie zur vertikalen Diagonalen notwendigerweise gestört. Die verbleibenden Leerstellen sind Rauten
oder stern-oder kronen-förmige Figuren. Auch nach Füllung der Zehnecke und Sechzehnecke haben Fünfecke
mit gemeinsamer Seite nie die gleiche Farbe. Und auf jedem Schildkröten-Weg wechseln sich geradzahlige und
ungeradzahlige Richtungszahlen ab.

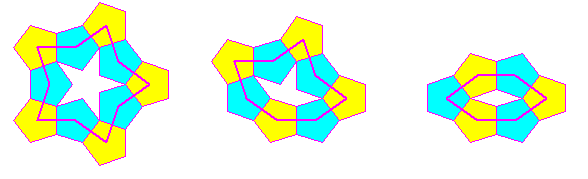
Hier werden die drei geschlossenen doppelpunkt-freie Fünfeck-Pfade mit den Richtungszahl-Differenzen
9393939393, 13939311 und 131131 gezeigt, deren Innenfigur ein Stern, ein kronenförmiges Polygon bzw.
eine Raute sind. Neben einem Pfad mit den Richtungszahl-Differenzen 9393193931 sind dies die geschlossenen
doppelpunkt-freie Fünfeck-Pfade mit den kleinsten Eckenzahlen. Wir nennen die durch die drei gezeigten
roten Pfade bestimmten Kacheln 'Stern', 'Krone' bzw. 'Boot' der Stufe 1 (andere Stufen werden unten erklärt).
Im Folgenden soll der Übergang zu nichr periodischen Kachelungen beschrieben werden, die sich ergeben, die
sich durch folgenden Übergang aus der Kepler-Kachelung ergeben:

1. Die zehn- und sechzehn-eckigen Leerstellen werden wie bei der Kepler-Raute gefüllt.
2. Die Fünfecke werden ersetzt durch die Strecken zwischen den Mitten von Fünfecken mit gemeinsamer Seite.

Die Gleitschau zeigt Erweiterungen von Teilen der gefüllten Kepler-Raute durch regelmäßige Fünfecke,
bei denen die Leestellen alle die Form einer Raute oder einer kronen- oder sternförmigen Figur haben.
Durch Verbindung der Mitten ergeben sich dabei die oben beschriebenen Stern- Kronen- oder Boot-
Kacheln 1. Stufe (blau, grün bzw. gelb). Die farbig unterlegte Kachelung nennen wir in Bild 1 bzw. 2
'Stern 2. bzw. 3.Stufe', in Bild 3 bzw. 4 'Krone 2. bzw. 3. Stufe' und in Bild 5 bzw. 6 'Boot 2. bzw. 3. Stufe'.
Bild 7 zeigt, dass eine Verbindung eines Sterns 3. Stufe mit einer Krone 3. Stufe die Kepler-Raute ganz
überdeckt. Dabei überlappen sich Stern und Krone 3. Stufe in zwei Boot-Kacheln 2. Stufe.

Die Animation und die in der Gleitschau folgenden Bilder verdeutlichen den Zusammenhang zwischen
der Kepler-Kachelung und einem Stern 3. Stufe.