Es lebe die Geometrie!

Archimedische Körper ohne Symmetrie-Ebenen

Es gibt zwei Typen von archimedischen Körpern ohne Symmetrie-Ebenen, nämlich den Cubus simus
und das Dodecaedron simum, auch abgeplatteter oder abgeschrägter Würfel bzw. Dodekaeder genannt.
Auch diese ergeben sich mit einer Kachelung, die aus der Würfel- bzw. Ikosaeder-Kachelung abgeleitet
ist. Und auch hier geht man zur Bestimmung eines A-Eckpunkts von einem gelb gezeichneten Punkt D in
dem Ausgangs-Dreieck ABC aus. Während man dort aber D an den Dreickseiten spiegelte, muss man
bei den nun betrachteten Kachelungen den Punkt D um die Dreiecks-Eckpunkte drehen, und zwar mit dem
Doppelten der Innenwinkel als Drehwinkel. Die Spiegelungen an den Dreieck-Seiten wird also durch die
Hintereinanderschaltung der Spiegelungen an je zwei Dreiecks-Seiten ersetzt. Gelbe A-Eckpunkte gibt es
dann nur in den positiv orientierten Dreiecken der Ausgangs-Kachelung.

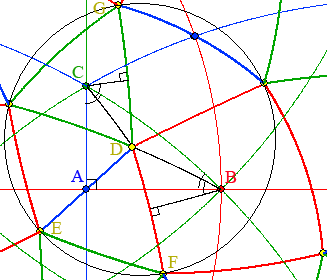
Die obenstehende Zeichnung zeigt das Ausgangsdreieck ABC der Würfel-Kachelung mit dem Punkt D,
der die abgeleitete Kachelung für den Cubus simus bestimmt. Der Punkt F entsteht aus D durch die
Hintereinanderschaltung der Spiegelungen an den Kreisbögen BC und BA. Darum stimmen die nicht-
euklidischen Abstände von BD und BF überein, und der Winkel zwischen dem Kreisbogen BD und dem
Lot von B auf DF ist so groß wie der zwischen BC und BA. F ist also das Bild von D bei der Drehung
um B mit dem Doppelten vom Winkel CBA als Drehwinkel. Der Fußpunkt des Lots von B auf DF ist
der nicht-euklidische Mittelpunkt von D und F. Durch Hintereinanderschaltung der Spiegelungen an den
Kreisbögen CA und CB ergibt sich aus D der Punkt G, und E ist das Bild von D bei Spiegelung an A.
Damit die abgeleitete Kachelung, die aus D durch Drehungen entsteht, zu einem archimedischen Körper
gehört, müssen die nicht-euklidischen Bogen-Abstände DE, DF und DG gleich groß sein. Da FE das
Bild von DG bei der Drehung um B ist, ist auch der Bogen-Abstand FE gleich groß, so dass folglich das
Dreieck EFD (nicht-euklidisch) gleichseitig ist.

In der euklidischen Dreiecks-Geometrie entsprechen dem Punkt D die beiden isodynamischen Punkte
X(15) und X(16) in der 'Encyclopedia of triangle centers'. Dies sind die Schnittpunkte der Apollonius-
Kreise des Basis-Dreiecks. Sie liegen auf der Verbindungsgeraden des Umkreis-Mittelpunkts mit dem
Symmedian-Punkt.

Die Berechnung des isodynamischen Punktes D bei den Großkreis-Kachelungen wird unten erläutert.

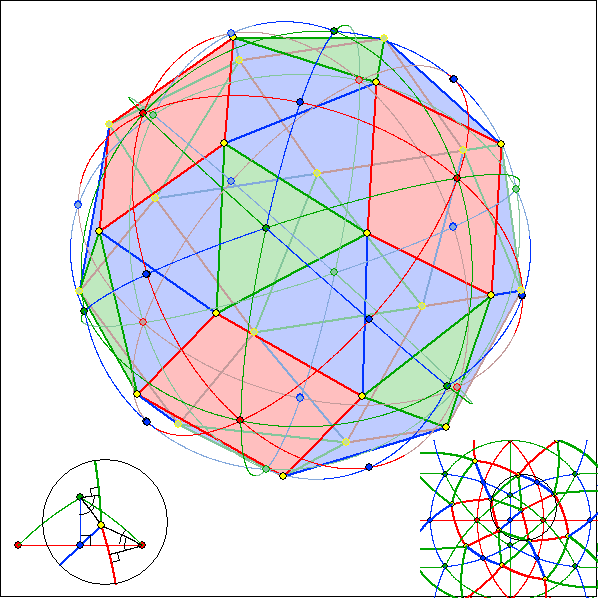
Bild 1 der Gleitschau zeigt den Cubus simus mit dem zugehörigen Poincare-Modell unten rechts
und einem Ausschnitt daraus mit dem Ausgangs-Dreieck ABC und dem gelben Punkt D unten
links. Dass keine Symmetrie-Ebenen vorkommen erkennt man daran, dass die blauen Dreiecke
links herum um die roten Quadrate herumführen. Im folgenden Bild 2 führen sie rechts herum, da
hier das Ausgangs-Dreieck ein Spiegelbild des Ausgangs-Dreiecke von Bild 1 ist. Die gelben Punkte
liegen dann alle in negativ orientierten Dreiecken. Bild 3 und 4 zeigen die Körper ohne die Seiten-
Bögen der Ausgangs-Kachelung, in Bild 5 und 6 sind die Kanten-Bögen hinzugefügt. Bild 7 und 8
geben das Poincare-Modell an und Bild 9 und 10 das Klein-Modell.

Diese Abfolge der Bilder wiederholt sich für die Ikosaeder-Kachelung und die Tetraeder-
Kachelung. Die Tetraeder-Kachelung ergibt ein Ikosaeder, also einen archimedischen Körper
mit Symmetrie-Ebenen, wenn man die Färbung unberücksichtigt lässt. Das liegt daran, dass das
Ausgangs-Dreieck mit den Innenwinkeln 90°, 60° und 60° symmetrisch ist.

Berechnung des isodynamischen Punktes D bei Großkreis-Kachelungen:

Wir kürzen wie auf der Seite 'Archimedes 2' die Wurzel mit w ab und mit v.
Im Klein-Modell hat dann die Seitengerade BC die Gleichung . Das Koordinaten-
Tripel von D in der Ebene z = 1 sei (x ; y ; 1). Nach der Seite 'Ikosaeder-Kachelung' ist dann das Bild
von D bei der Spiegelung an der Geraden BC das Tripel, das man erhält, wenn man in dem Term
die Komponenten zusammenfasst und das entstehende Tripel
durch die dritte Komponente teilt. Es ergibt sich .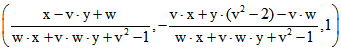
Durch Spiegelung an der Geraden AB entsteht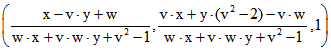
als Tripel des Punktes F in obiger Zeichnung. Da das Dreieck EFD gleichseitig ist, muss die Gerade AF
orthogonal zu AD sein, und zwar sogar euklidisch orthogonal, da für die Geraden durch den Ursprung
die elliptisch orthogonalen Geraden auch euklidisch orthogonal sind, und umgekehrt. Daraus folgt
.

Im Klein-Modell wird der Abstand zweier Punkte und durch die Länge
des kleineren Bogens zwischen den P und Q zugeordneten Punkten auf der Kugel berechnet. Er ist gleich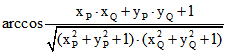
.
D und A haben darum im Klein-Modell den elliptischen Abstand .
Wegen ist das Doppelte davon . Dies ist der
elliptische Abstand von E und D. Der Abstand von D und F ist
.
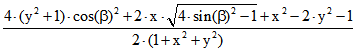
Da E von D den gleichen elliptischen Abstand wie von F hat, folgt .


Aus den in den beiden vorangegangenen Abschnitten hergeleiteten Gleichungen folgt wegen

.
Es ist also . Die Einsetzung in führt zu
. Wegen muss also
Null werden. Für y ergeben sich die Lösungen
mit .

Diese Lösungen sind für alle drei reell, für und aber nur bei k = 2.
Im Fall k = 2 erhält man im Klein-Modell folgende Koordinaten für D:





Die entsprechenden Koordinaten sind im Poincare-Modell für