Es lebe die Geometrie!

Drehpunktfunktion bei Traktrix und Kettenlinie
--> Erklärung zur Drehpunktfunktion (https://www.vivat-geo.de/Pdf-Dateien/Drehpunktfunktion.pdf)

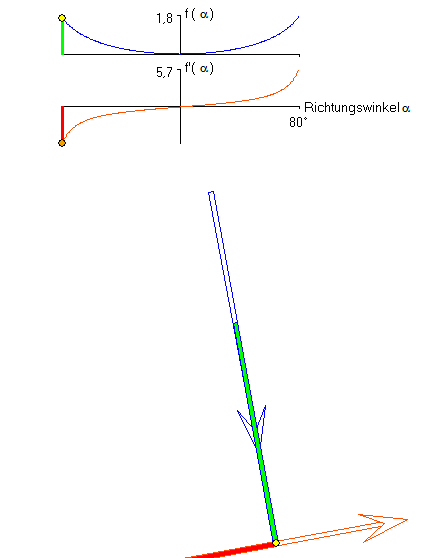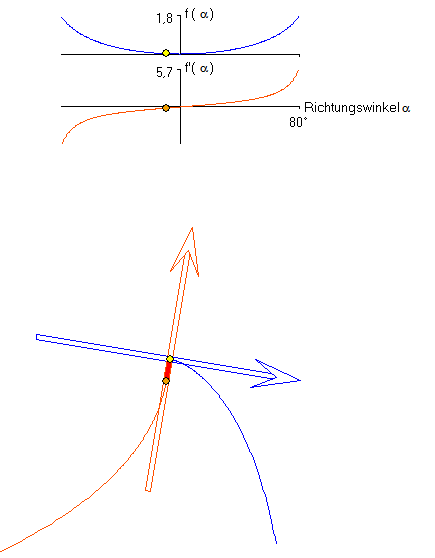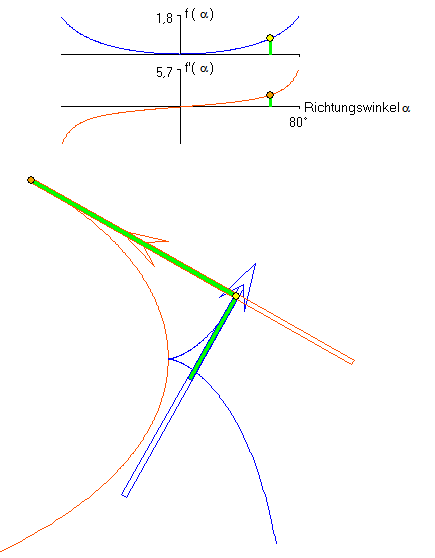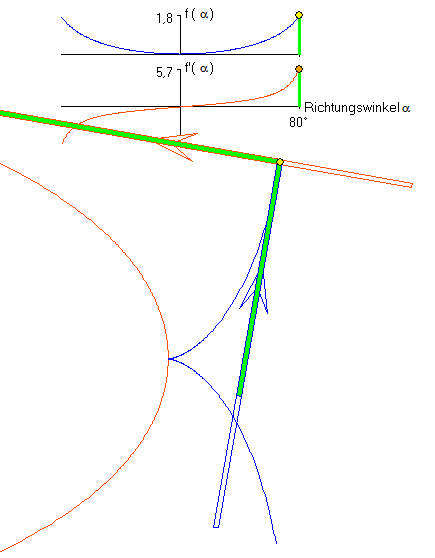
f(a) = - ln(cos(a)) und f '(a) = tan(a)
Jede der beiden Teile der dunkelblauen Kurve ist eine Traktrix (Schleppkurve). Sie ensteht als Spur
eines schweren Gegenstandes, der mit einem Seil gezogen wird, so dass sich der Ziehende auf einer
Geraden bewegt, die nicht durch den Gegenstand verläuft. Die dunkelblaue Kurve wird durch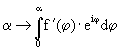
beschrieben. Der Betrag von f(a) gibt die Länge des Traktrix-Bogenstücks von der
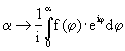Spitze bis zu dem Punkt mit dem Steigungswinkel a an. Die orangefarbene Kurve ist eine (um 90° gedrehte)
Kettenlinie mit der Kurvenfunktion 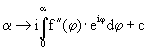. (c ist hierbei der Kurvenpunkt zu a = 0.)
Die Kettenlinie ist die Evolute der Traktrix.

Drehpunktfunktion , also
Die dunkelblaue Kurve ist die Kettenlinie, die hellblaue eine Traktrix. Die orangefarbene Kurve
ist die Evolute der Kettenlinie.

Drehpunktfunktion 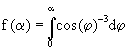, also
Die dunkelblaue Kurve ist die Parabel , die orangefarbene ihre Evolute und die hellblaue
eine Evolvente.