Es lebe die Geometrie!

--> Pdf-Datei ' Kachelungen, die mit Nachbar-Bewegungen erzeugt werden'
(https://www.vivat-geo.de/Pdf-Dateien/Kachelungen.pdf)

Es werden in der unten angegebenen Bildfolge 46 Typen periodischer Kachelungen mit lauter kongruenten
Kacheln angegeben. Jeder Typ ist durch eine Signatur und eine Folge von Klassenwinkeln bestimmt. Die
Signatur gibt an, wie aus einer Kachel eine dazu kongruente Nachbar-Kachel durch eine Bewegung
(Kongruenzabbildung) entsteht. Die Klassenwinkel sind die Summen von Innenwinkeln einer Kachel bei
gleichfarbig markierten Eckpunkten. Sie können nur die Werte 30°, 45°, 60°, 90°, 120°, 180° und 360°
annehmen. Eckpunkte P und Q sind in der gleichen Farbe gezeichnet, wenn es eine Hintereinanderschaltung
von Nachbar-Bewegungen gibt, die P in Q abbildet.

Es gibt 37 Signaturen, die zu einer Kachelung führen können und nicht durch eine Umnummerierung
auseinander hervorgehen. Den Beweis findet man in der oben angegebenen Pdf-Datei.
Von den 37 möglichen Signaturen lassen sechs mehr als eine Klassenwinkel-Kombination zu.

Zu jedem Typ werden zwei Beispiele angegeben, wobei das zweite die besondere Eigenschaft hat,
dass die an einem Eckpunkt zusammenstoßenden Kacheln dort alle gleich große Innenwinkel haben.
Man nennt sie auch 'Laves-Kachelungen'. In einigen Fällen ist der Typ durch Signatur und Klassenwinkel-
Kombination so eingeschränkt, dass das möglichst allgemeine erste Beispiel mit dem zweiten übereinstimmt.

Bei jeder Kachel sind die Seiten durchnummeriert, gegen oder im Uhrzeigersinn. Die Seite mit der Nummer 1
wird mit einem Halbpfeil markiert. Jeder Seitennummer ist ein bestimmter Typ einer Nachbar-Bewegung
zugeordnet. Eine zuerst ausgelegte Kachel sei z. B. ein Trapez. Die Seiten werden mit den Zahlen 1 bis 4
gegen den Uhrzeigersinn durchnummeriert. Der Seite 1 sei die Achsenspiegelung an dieser Seite zugeordnet,
der Seite 2 die Punktspiegelung am Mittelpunkt dieser Seite, der Seite 3 die Achsenspiegelung daran und der
Seite 4 die Punktspiegelung an ihrem Mittelpunkt. Dies wird kürzer durch die Signatur -12-14 beschrieben.
Es ergibt sich die 15. Kachelung in der Bildfolge, wenn man die Bilder von bei diesen Bewegungen als
Nachbar-Kacheln von benutzt.

Die 20. Kachelung hat die Signatur -2-134. Dies bedeutet, dass die Seite 2 der Kachel mit einer
Gleitspiegelung auf die Seite 1 von abgebildet wird und die Seite 2 durch die dazu inverse Gleitspiegelung.
Die Seiten 3 und 4 werden durch Punktspiegelungen am Mittelpunkt abgebildet. Die 27. Kachelung hat die
Signatur 2143. Das heißt, dass die 2. Seite in die 1. um einen Eckpunkt gedreht wird und die 1. in die 2. durch
die inverse Drehung. Entsprechend wird die 4. Seite in die 3. gedreht. In der Kachelung 34 mit der Signatur
-15342 wird bei einem Fünfeck die 5. Seite in die 2. verschoben und die 2. in die 5. An der 1. Seite wird
gespiegelt, die 3. und 4. gehen durch zueinander inverse Drehungen auseinander hervor.

Das schwarz gezeichnete Randmuster im Hintergrund gibt jeweils eine Zusammenfassung mehrerer Kacheln zu
einer größeren Kachel an, mit der die Ebene allein durch Verschiebungen überdeckt werden kann.

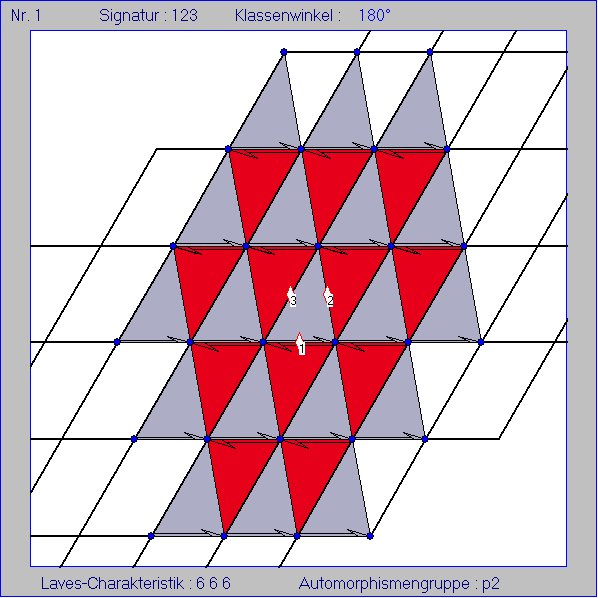
Die in diesen Bildern angegebenen Kachelungen lassen sich zu einer vollständigen Überdeckung
der ganzen Ebene fortsetzen. Dabei stoßen in Eckpunkten immer gleich viele Kacheln zusammen.
Diese Anzahlen werden mit der Laves-Charakteristik angegeben.
Jede Nachbar-Bewegung einer beliebigen Kachel bildet jede Kachel in eine andere Kachel der
Kachelung ab; sie ist also ein Automorphismus der Kachelung. Jeder Automorphisnus der Kachelung
ist als Hintereinanderschaltungen der Nachbar-Bewegungen der zuerst ausgelegten Kachel (oder einer
anderen) dargestellbar. Jede Automorphismengruppe ist eine der 17 kristallographischen Ebenen-
Gruppen, deren Bezeichnung am unteren Rand angegeben ist.