Es lebe die Geometrie!
Hauptmenü
- Home
- Geometrie 1
- Geometrie 2
- Epizykeltheorie
Kreis- Gerade
Geometrie 2 > konjugierte Polaren
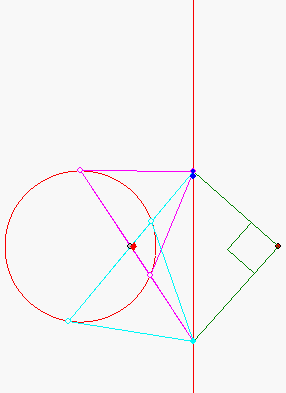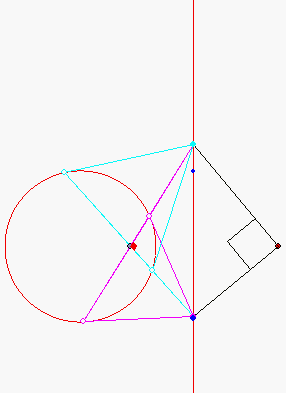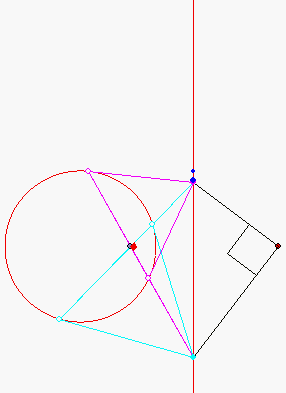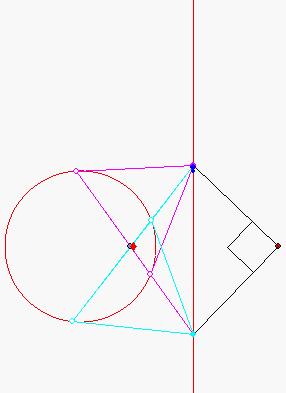
Konjugierte Polaren bei der Kreis-Geraden-Kubik
Durch den dunkelblauen Punkt A auf der rot gezeichneten senkrechten Geraden g sind zwei Tangenten an den Kreis k gezeichnet. Die Gerade durch die beiden Berührpunkte ist die 'Polare' von A. Sie schneidet g in einem hellblauen Punkt B. Die Polare von B geht dann durch A. Der rote Punkt M rechts von g wird 'Maßpunkt' genannt. Der Winkel AMB ist stets ein rechter. M liegt auf der Lotgeraden h vom Kreismittelpunkt auf g. Wenn der Schnittpunkt von g und h mit Z bezeichnet wird, so gilt:
M hat von Z denselben Abstand wie der Berührpunkt einer Tangente, die von Z aus an der Kreis gelegt wird.
Untermenü