Es lebe die Geometrie!

Geschwindigkeiten und Perioden beim Billard in der Ellipse

Die Animation zeigt innerhalb der roten Ellipse die blaue Bahnkurve (Trajektorie) einer Billardkugel mit
der Periode 4, die also nach vier Reflexionen an der Ellipse wieder bei der Ausgangssehne ankommt.
Die vier verschiedenen Sehnen berühren dann die blaue Ellipse, deren Brennpunkte mit denen der roten
übereinstimmen. Nach dem Satz von Poncelet hat dann jede Trajektorie, deren erste Sehne die blaue
Ellipse berührt, ebenfalls die Periode 4. Die Pole der Sehnen liegen hier auf einem Kreis mit der
Eigenschaft, dass die rote Ellipse von jedem Punkt des hellblauen Polkreises unter dem Sehwinkel 90°
erscheint. (Siehe dazu das ' Arnoldsche Problem'.) Der Radius des Kreises stimmt mit dem Abstand eines
Haupt-Scheitelpunkts von einem Neben-Scheitelpunkt der roten Billard Ellipse überein. Die grauen
Tangenten in den vier Reflexionspunkten bilden eine rechteckige Billard-Fläche, zu der die blaue Bahnkurve
ebenfalls eine Billard-Trajektorie ist, deren Seitenlängen sich aber verändern.

Bei der Bewegung des Anfangspunkt der Trajektorie auf der roten Ellipse mit der Geschwindigkeit
bewegt sich der Endpunkt der ersten Sehne mit der Geschwindigkeit , wobei
und die Größen der Winkel zwischen der Sehne und den Tangenten in den Endpunkten sind. (Diese
Geschwindigkeiten sind in der Animation proportional zur Länge der roten Pfeile.) Zur Begründung der
Formel betrachten wir das Dreiseit aus den Tangenten und der Sehne. Es hat die Höhe h durch den Pol und
die Höhenabschnitte und . Es gilt . Das Verhältnis der Komponenten
der Geschwindigkeiten senkrecht zur Sehne (blaue Pfeile) ist und stimmt mit dem Verhältnis
der Höhenabschnitte überein. Daraus folgt die Beziehung zwischen und .

Die hier dargestellten blauen Billard-Trajektorien sind zum Teil periodisch (mit den Perioden 8, 7, 6, 5, 4
und 3) und zum Teil nicht. Die Trajektorien-Ellipsen haben alle die gleichen Brennpunkte, beim Übergang
von einer Periode zur nächsten ändern sich aber ihre Achsenlängen. Diese bleiben konstant, wenn bei fester
Periode nur der Anfangspunkt verrückt wird. Dies ist eine Folgerung des Satzes von Poncelet.

Über der Hauptachse der Billard-Ellipse als Durchmesser wurde der gelb-graue Hilfskreis gezeichnet. a und
b seien die Halbachsen-Längen der Billard-Ellipse. sei der Punkt des Hilfskreises,
dessen Ortsvektor den Richtungswinkel hat. Dann ist der Punkt der Ellipse, der
aus R durch Streckung in y-Richtung mit dem Faktor entsteht. Wenn R sich auf dem Kreis bewegt, hat sein
Geschwindigkeits-Vektor die Form mit einem geeigneten Faktor f zu Längen-
Anpassung. R' bewegt sich dann mit dem Geschwindigkeits-Vektor .

Der oben in der Animation angegebene Graph gehört zu der Funktion , wobei
den Richtungswinkel zu einem Punkt R des Hilfskreises angibt und die numerische Exzentrizität der blauen
Trajektorien-Ellipse, also das Verhältnis vom Abstand der Brennpunkte zu der Länge der Hauptachse.
legt einen Geschwindigkeits-Betrag fest, der dem Punkt R zugeordnet wird. Er wird durch die Länge des
gelben bzw. orangefarbenen Pfeils dargestellt. Dazu passen die Längen der roten Geschwindigkeits-Vektoren
zu Punkten der Billard-Ellipse. Wenn zwei Punkte der Billard-Ellipse die so ihrem Ort zugewiesene
Geschwindigkeit einhalten, dann ändert sich die Trajektorien-Ellipse der zugehörigen Sehne nicht. Das soll
mit dem unten folgenden Satz gezeigt werden.

Da die Animation in verschiedenen Phasen unterschiedlich schnell abläuft, ist dabei die Geschwindigkeit der
markierten Kreispunkte nicht immer die ihrem Ort zugewiesenen Geschwindigkeit, ihr Verhältnis stimmt aber
mit den vom Ort bestimmten Geschwindigkeiten überein.
Der zweite Graph gehört zur Integralfunktion . Dabei gibt die Zeit an, die ein Punkt
bei Einhaltung der vom Ort vorgeschriebenen Geschwindigkeit auf dem Kreis braucht, um vom Ort zum
Ort zu kommen. Die Höhe des grauen Rechtsecks in dem Graphen ist darum die Zeit, die
für den Weg vom jeweils aktuellen Ort des gelben Punktes R zu dem des orangefarbenen Punktes S benötigt
wird. Sie ist bei der dargestellten Bewegung eine Konstante im Fall, dass die zugehörigen Punkte R' und S' auf
der Billard-Ellipse Eckpunkte einer Trajektorie mit der Periode n sind. Die Konstante ist dann , wobei
die Zeit für einen vollen Umlauf ist. Wegen der verschiedenen Werte von bei den Trajektorien-Ellipsen ist T
für die verschiedenen Werte von n unterschiedlich. Es ist .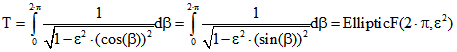
Mit Hilfe der Sehne, welche die Trajektorien-Ellipse in einem Hauptscheitelpunkt berührt, erkennt man, dass
im Fall der Periode n gelten muss: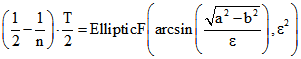

.


Zur Begründung:
Satz : Die rote Basis-Ellipse E habe die Gleichung und eine Billard-Trajektorie (periodisch
oder nicht) berühre die Ellipse F mit der Gleichung . k sei eine positive Konstante. Jedem
Punkt auf E sei die Geschwindigkeit 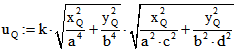zugeordnet.
Bewegen sich dann die Endpunkte einer Sehne der Trajektorie mit der ihrem Ort zugeordneten
Geschwindigkeit, dann ändert sich die Trajektorien-Ellipse nicht.

Beweis : Die Streckung in y-Richtung bildet E auf den Kreis mit dem Radius a ab und
F auf die Ellipse F' mit der Gleichung . Sei und . Da die
Brennpunkte von E und F übereinstimmen, gilt . Daraus errechnet man die Gleichung
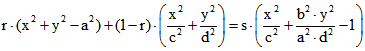. Der Term der Ellipse, die durch Streckung
aus F entsteht, ist also Linearkombination der Terme des a-Kreises und der Null-Ellipse mit der Gleichung
. Jedem Punkt R des a-Kreises sei die Geschwindigkeit zugeordnet.
Aus Satz 2 in der Pdf-Datei ' Bewegungen auf dem Kreis und der Satz von Poncelet' folgt dann:

Wenn sich die Endpunkte einer F' berührenden a-Kreis-Sehne mit der ihrem Ort zugeordneten
Geschwindigkeit bewegen, dann bleibt die Sehne stets in Berührung mit F'.

Der zu gehörige Geschwindigkeitsvektor ist der Vektor . Die Rück-Streckung in
y-Richtung bildet R in einen Punkt Q von E ab, so dass gilt.
Dabei wird der Geschwindigkeitsvektor in abgebildet,
wobei 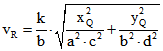gilt. Der Betrag dieses Geschwindigkeitsvektors ist
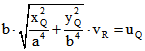, was zu zeigen war.

Der hier benutzte a-Kreis ist der gelb-graue Hilfskreis der Animation. Wenn der Ortsvektor des Punktes R
den Richtungswinkel hat, dann ist und

.
Für ergibt sich die oben angegebene Formel.

Die Animation zeigt Billard-Trajektorien mit der Perioden 4 und 8, deren Sehnen die Strecke
zwischen den Brennpunkten der Billard-Ellipse kreuzen. Die Trajektorien berühren darum
Hyperbeln mit den gleichen Brennpunkten