Es lebe die Geometrie!

Reuleaux-Dreieck

-->Figuren mit konstanter Breite
https://www.vivat-geo.de/Pdf-Dateien/Gleichdick.pdf

Das Reuleaux-Dreieck ist ein Gleichdick, das nach dem Ingenieur Franz Reuleaux (1829-1905) benannt ist.
Es ist ein regelmäßiges Kreisbogen-Dreieck mit den Innenwinkeln 120°.
Die Form fand beim Wankel-Motor Verwendung.

Das Reuleaux-Dreieck wird hier dadurch als Drehpunkt-Kurve erzeugt, dass der gelbe Drehpunkt
zwischen den Werten 1 und -1 hin und her wechselt. Die rote Ortslinie der Pfeilspitze setzt sich dann aus
Kreisbögen zusammen. Die Drehpunktfunktion ist dieTreppenfunktion
und das Reuleaux-Dreieck die zugehörige 1-Kurve .

Hier werden die Verbindungsstrecken der Berührpunkte paralleler Stützgeraden hellblau eingezeichnet. Die
Mittelpunkte der umschließenden Quadrate liegen anders als beim Steiner-Gleichdick nicht auf einem Kreis.
Wenn die Eckpunkte des Reuleaux-Dreiecks die Punkte , und sind und der Richtungswinkel
des Pfeils ist, dann kann die Spur des Quadrat-Zentrums folgendermaßen beschrieben werden: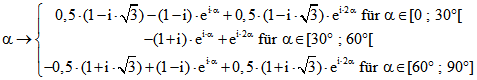



Die so beschriebenen drei Teile schließen sich zu einer Kurve zusammen, die bei einer vollen Drehung des
Pfeils viermal durchlaufen wird. Jeder der drei Teile ist ein Abschnitt einer pascalschen Schnecke. Diese
ergibt sich als Bahnkurve einer Überlagerung zweier gleichförmiger Kreisbewegungen, bei denen die eine
Winkelgeschwindigkeit doppelt so groß ist wie die andere.

Die Animation zeigt die Minkowski-Addition eines Reuleaux-Dreiecks mit einen Punktspiegelungs-Bild
davon. Wie bei jedem Gleichdick entsteht dabei ein Kreis, dessen Umfangslänge doppelt so groß ist
wie die des Gleichdicks.

Die Animation zeigt die roten s-Kurven der treppenförmigen Drehpunktfunktion zur Erzeugung
des Reuleaux-Dreiecks für s-Werte zwischen Null und Eins. Sie entsprechen den Evolventen der
Steiner-Zykloide. Bei allen s-Kurven sind die Tangente-Rechtecke Quadrate mit der Seitenlänge
2s, also unabhängig vom Richtungswinkel (wie bei der Steiner-Zykloide). Für s = 0 schrumpft das
Tangenten-Quadrat zu einem Punkt, welcher der Mittelpunkt der Tangenten-Quadrate mit gleicher
Orientierung bei allen s-Kurven ist. Dieser Punkt ist der Schnittpunkt einer Tangente der hellblau
gezeichneten Null-Kurve mit der eindeutig bestimmten dazu senkrechten Tangente. Die Null-Kurve
ist ein regelmäßiges Kreisbogen-Dreieck mit der Innenwinkel-Größe 0°. Die Ortskurve der
Quadrat-Mittelpunkte ist also der geometrische Ort der Schnittpunkte senkrechter Tangenten
zu diesem Kreisbogen-Dreieck.